P3242 [HNOI2015] 接水果

题目链接

题意分析

这是一道花了一晚上+上午两个小时+下午两个小时干出来的题

真心不容易

首先 一看这道题的题面 对于多组询问求解第k小 就让人想到了整体二分

但是我们需要处理一个棘手的问题 怎么判断一条路径 u→v 被另外一条路径 x→y 覆盖呢？

---

这个我们我们可以使用dfs序解决

这里我们令dfn[u]为u的dfs序 siz[u]为以u为根的子树大小

令dfn[u]<dfn[v] dfn[x]<dfn[y]

1.lca(u,v)=u 也就是说u→v是一条深度单调递增的链

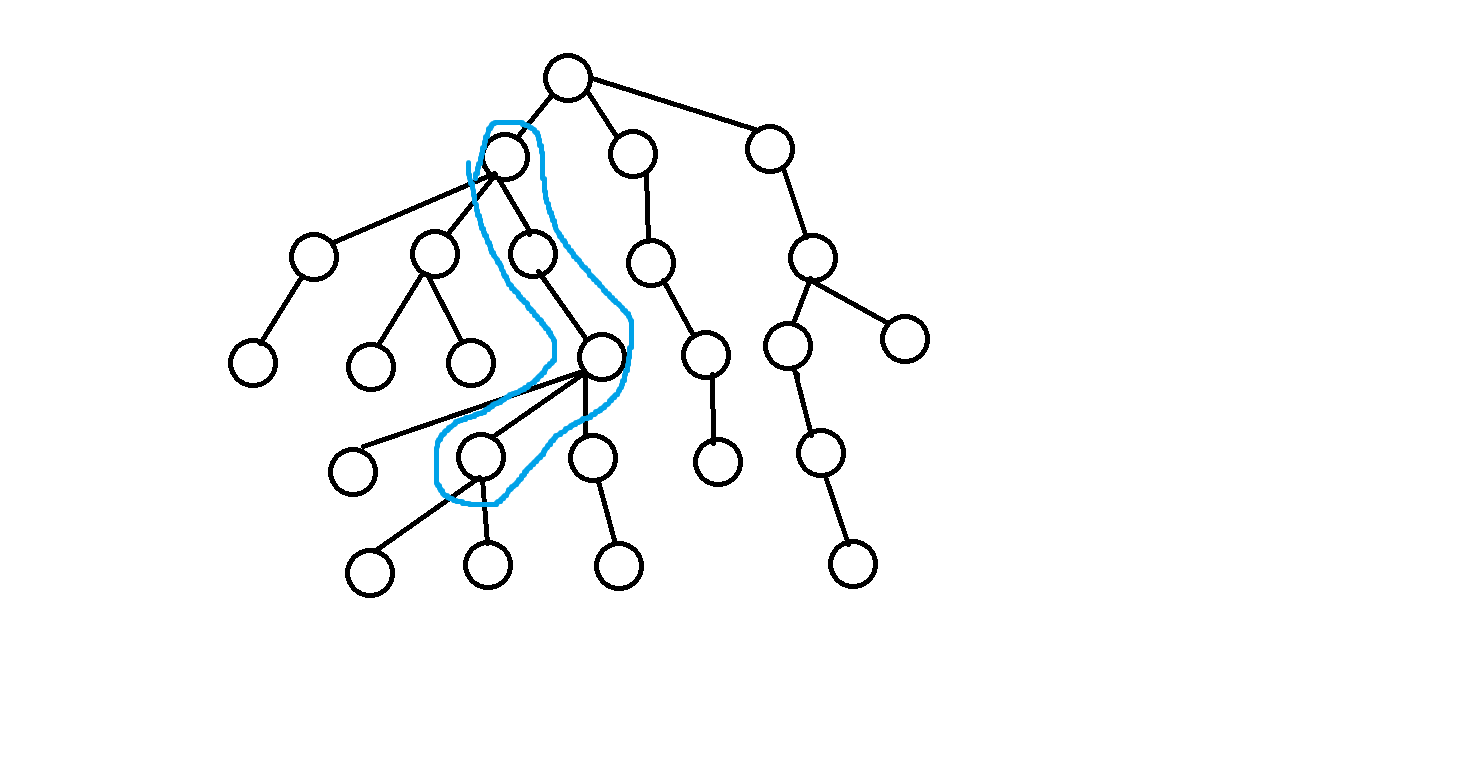
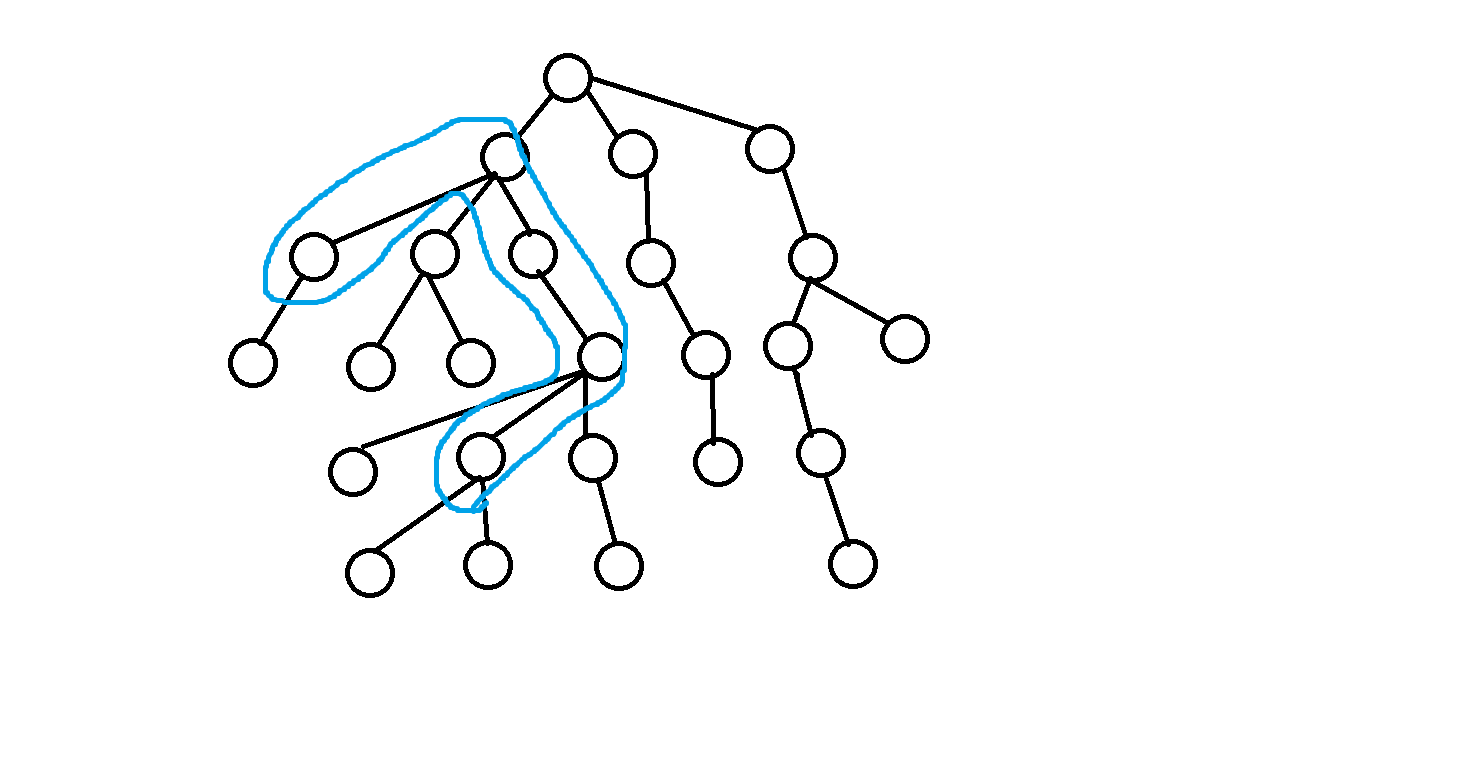
我们令z是从u到v所经过的第一个点

那么x与y必然一个属于以z为根的子树外的点 一个属于以v为根的子树

就是满足以下两个条件中的一个

1).1≤dfn[x]<dfn[z] dfn[v]≤dfn[y]≤dfn[v]+siz[v]-1

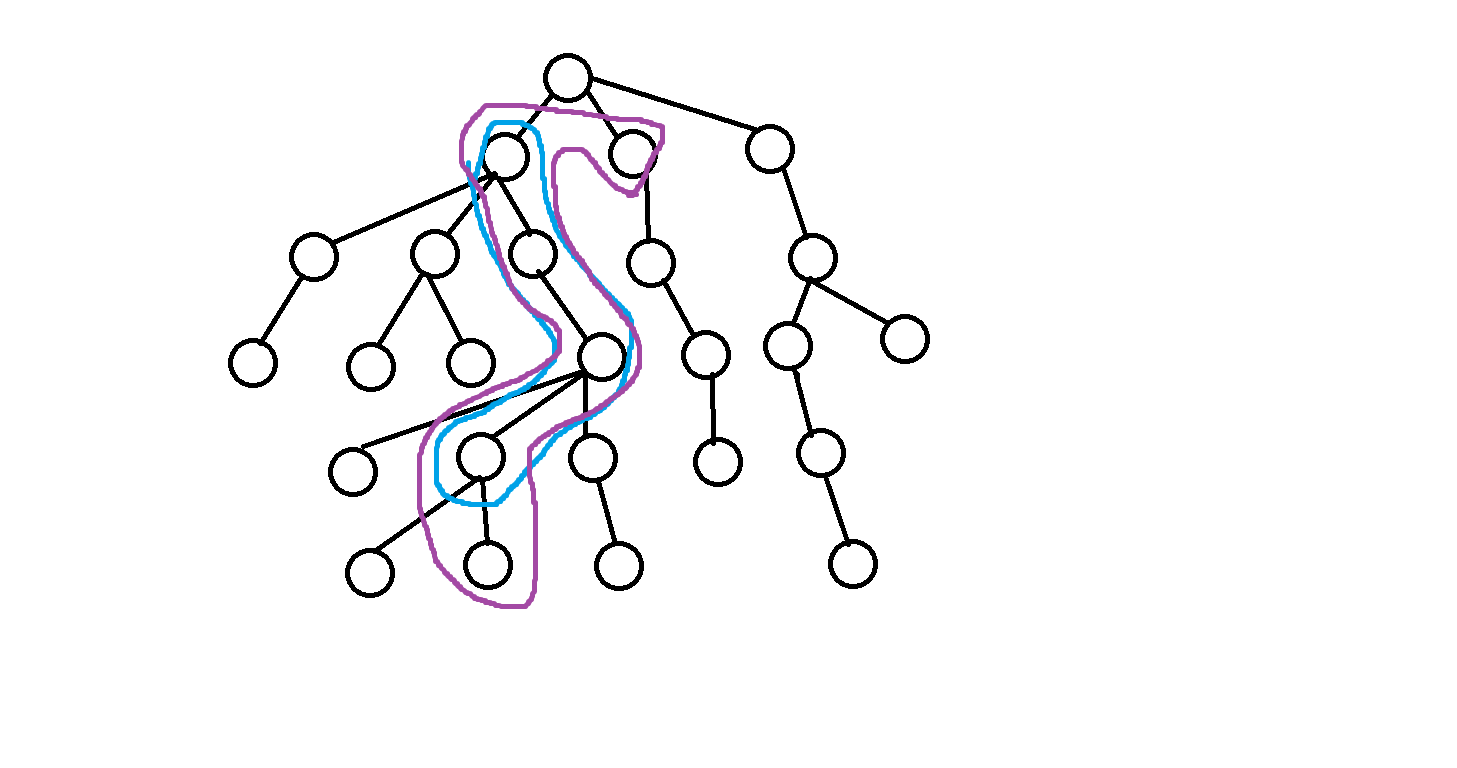
2).dfn[v]≤dfn[x]≤dfn[v]+siz[v]-1 dfn[z]+siz[z]-1<dfn[y]≤n

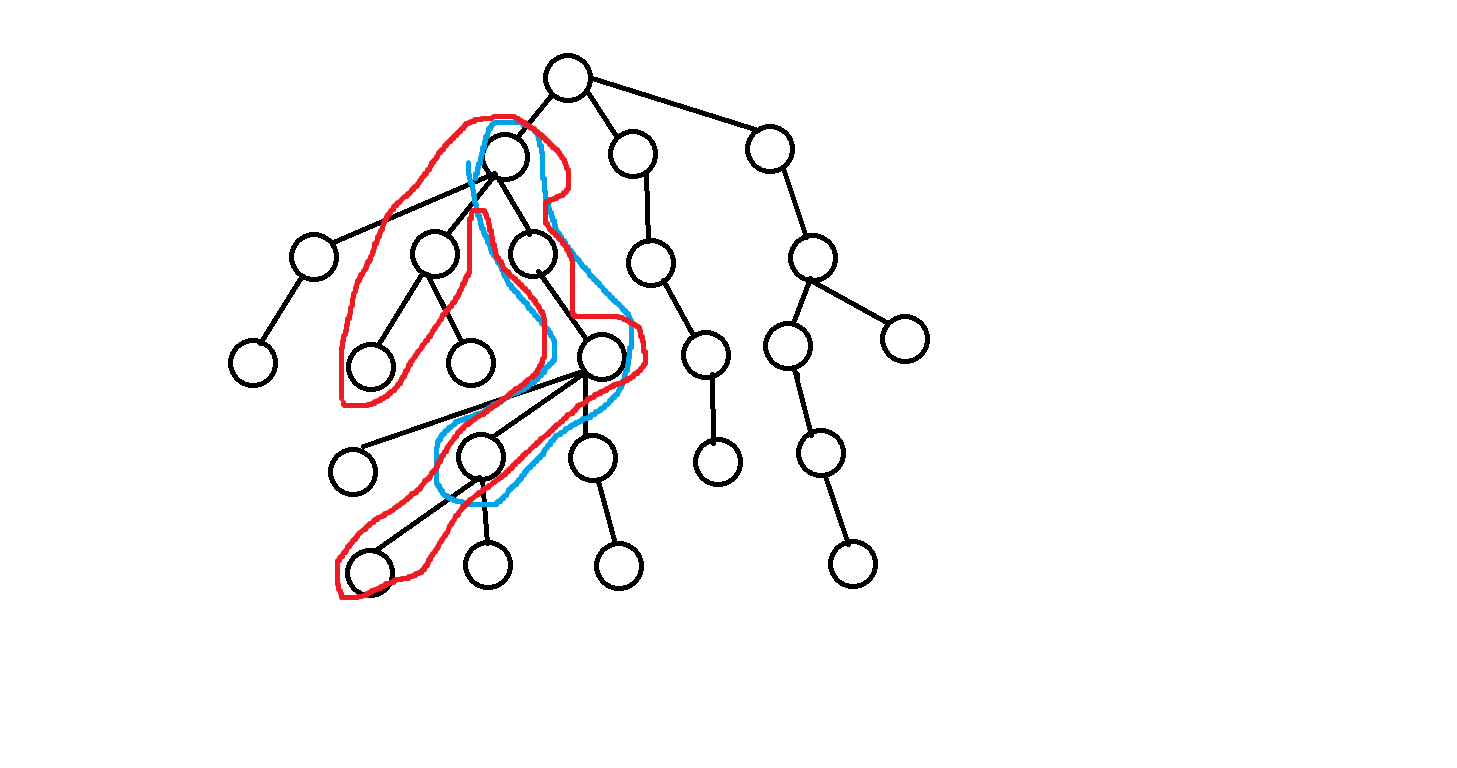
2.lca(u,v)!=u 也就是说u→v是一条深度先减少后增加的链

那么x与y必然一个属于以u为根的子树 一个属于以v为根的子树

---

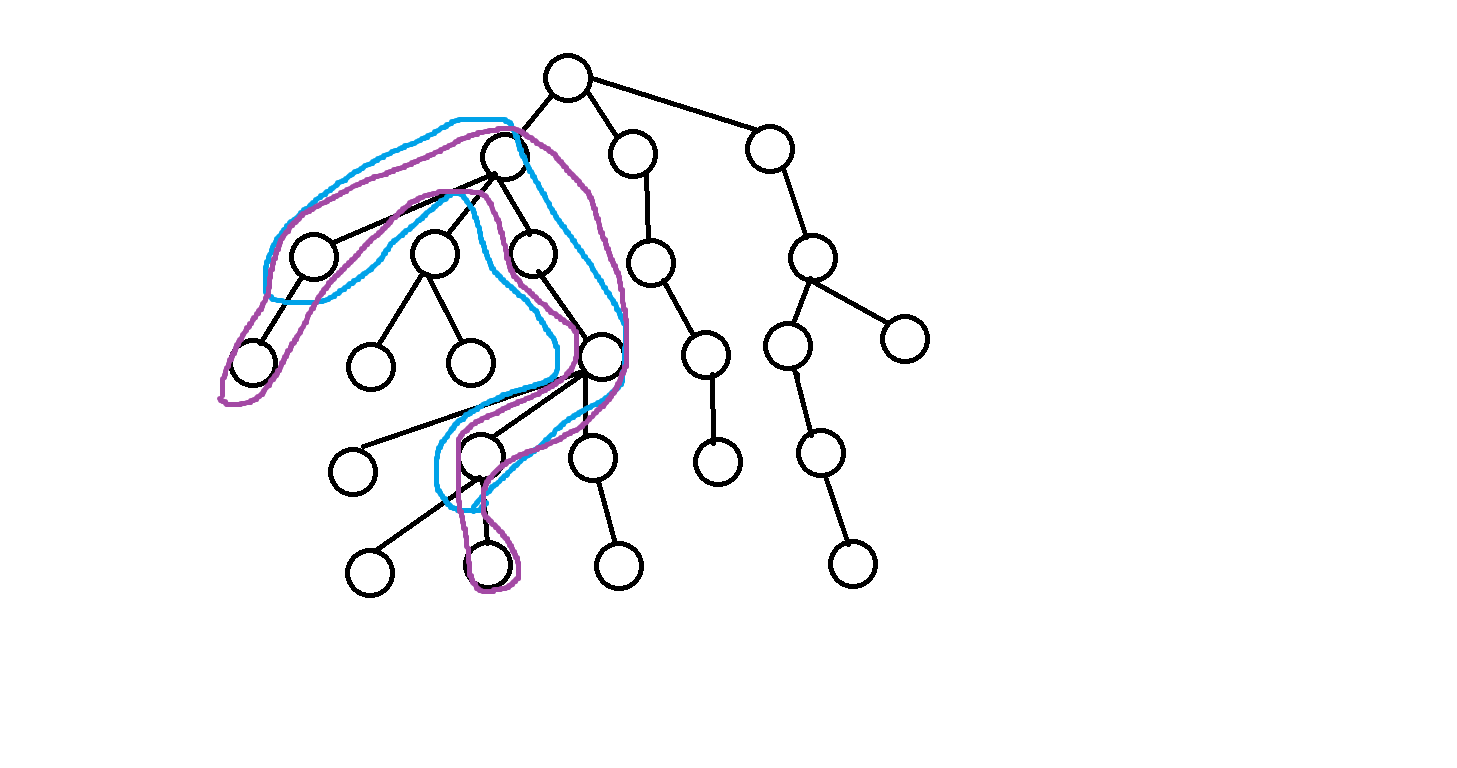
按照上述结论我们可以发现 实际上这就是一个二维数点问题 判断一个点被多少个矩形覆盖了 使用扫描线方法加以解决

这就是我们拿来进行整体二分的判断方式

这道题很多人说需要卡常 比如说使用树剖代替倍增求lca以及u→v的第一个点z

但是本蒟蒻使用倍增过了 可能是因为我比较帅吧(doge)

CODE:

#include<bits/stdc++.h>
#define N 500010
using namespace std;
int n,m,q,tot,cnt;
int to[N],nex[N],head[N];
int dep[N],fa[N][22];
int dfn[N],wt[N],siz[N];
vector<int> G[N];
struct Edge
{
	int u,v,w,knd,ex;
}e[N];
struct Temp
{
	int le,ri,at,d,knd;
	friend bool operator < (const Temp &A,const Temp &B)
	{return A.at==B.at ? A.knd<B.knd : A.at<B.at;}//我们需哦保证先修改再询问
}et[N];
int res[N],tre[N],vis[N];
struct Query
{
	int u,v,k,id,ans;
	friend bool operator < (const Query &A,const Query &B)
	{return A.id<B.id;}
}que[N],cdy[N],wzy[N];
void add(int x,int y)
{to[++tot]=y;nex[tot]=head[x];head[x]=tot;}
void dfs(int now,int fat) 
{
	dep[now]=dep[fat]+1;fa[now][0]=fat;
	for(int i=1;(1<<i)<=dep[now];++i)
	fa[now][i]=fa[fa[now][i-1]][i-1];
	
	siz[now]=1;dfn[now]=++cnt;wt[cnt]=now;
	
	for(int i=head[now];i;i=nex[i])
	{
		int v=to[i];
		if(v==fat) continue;
		dfs(v,now);
		siz[now]+=siz[v];
	}
}
int LCA(int nowx,int nowy)
{
	if(dep[nowx]<dep[nowy]) swap(nowx,nowy);
	for(int i=20;i>=0;--i)
	if(dep[fa[nowx][i]]>=dep[nowy]) nowx=fa[nowx][i];
	if(nowx==nowy) return nowx;
	for(int i=20;i>=0;--i)
	if(fa[nowx][i]!=fa[nowy][i])
	nowx=fa[nowx][i],nowy=fa[nowy][i];
	return fa[nowx][0];
}
void update(int x,int d)
{for(;x<=n;x+=x&-x) tre[x]+=d;}
int query(int x)
{int tmp=0;for(;x;x-=x&-x) tmp+=tre[x];return tmp;}
void solve(int lenow,int rinow,int le,int ri)
{
	if(lenow==rinow)
	{
		for(int i=le;i<=ri;++i) que[i].ans=lenow;
		return;
	}
	int mid=(lenow+rinow)>>1;cnt=0;
	for(int i=lenow;i<=mid;++i)
	{
		for(int j=0;j<(int)G[i].size();++j)
		{//开始扫描线处理修改以及询问
			int tmp=G[i][j];
			if(e[tmp].knd==2)
			{
				++cnt;
				et[cnt].at=dfn[e[tmp].u];et[cnt].le=dfn[e[tmp].v];et[cnt].ri=dfn[e[tmp].v]+siz[e[tmp].v]-1;et[cnt].d=1;et[cnt].knd=1;
				++cnt;
				et[cnt].at=dfn[e[tmp].u]+siz[e[tmp].u];et[cnt].le=dfn[e[tmp].v];et[cnt].ri=dfn[e[tmp].v]+siz[e[tmp].v]-1;et[cnt].d=-1;et[cnt].knd=1;
			} 
			else
			{
				++cnt;
				et[cnt].at=1;et[cnt].le=dfn[e[tmp].v];et[cnt].ri=dfn[e[tmp].v]+siz[e[tmp].v]-1;et[cnt].d=1;et[cnt].knd=1;
				++cnt;
				et[cnt].at=dfn[e[tmp].ex];et[cnt].le=dfn[e[tmp].v];et[cnt].ri=dfn[e[tmp].v]+siz[e[tmp].v]-1;et[cnt].d=-1;et[cnt].knd=1;
				++cnt;
				et[cnt].at=dfn[e[tmp].v];et[cnt].le=dfn[e[tmp].ex]+siz[e[tmp].ex];et[cnt].ri=n;et[cnt].d=1;et[cnt].knd=1;
				++cnt;
				et[cnt].at=dfn[e[tmp].v]+siz[e[tmp].v];et[cnt].le=dfn[e[tmp].ex]+siz[e[tmp].ex];et[cnt].ri=n;et[cnt].d=-1;et[cnt].knd=1;
			}
		}
	}
	for(int i=le;i<=ri;++i)
	{
		vis[i]=0;
		++cnt;
		et[cnt].at=dfn[que[i].u];et[cnt].le=dfn[que[i].v];et[cnt].ri=i;et[cnt].knd=2;
	}
	sort(et+1,et+cnt+1);
	for(int i=1;i<=cnt;++i)
	{//由于是区间修改 单点查询 所以我就使用了树状数组
		if(et[i].knd==1)
		update(et[i].le,et[i].d),update(et[i].ri+1,-et[i].d);
		else
		{
			int tmp=query(et[i].le);
			vis[et[i].ri]+=tmp;
		}
	}
	int cnta=0,cntb=0;
	for(int i=le;i<=ri;++i)
	{
		if(vis[i]>=que[i].k) cdy[++cnta]=que[i];
		else 
		{
			que[i].k-=vis[i];
			wzy[++cntb]=que[i];
		}
	}
	for(int i=le;i<=le+cnta-1;++i) que[i]=cdy[i-le+1];
	for(int i=le+cnta;i<=ri;++i) que[i]=wzy[i-le-cnta+1];
	solve(lenow,mid,le,le+cnta-1);solve(mid+1,rinow,le+cnta,ri);
}
int main()
{
	scanf("%d%d%d",&n,&m,&q);
	for(int i=1,x,y;i<n;++i)
	{
		scanf("%d%d",&x,&y);
		
		add(x,y);add(y,x);
	}
	dfs(1,0);
	for(int i=1;i<=m;++i)
	{
		scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
		if(dfn[e[i].u]>dfn[e[i].v]) swap(e[i].u,e[i].v);
		res[i]=e[i].w;
		int tmp=LCA(e[i].u,e[i].v);
		if(tmp!=e[i].u&&tmp!=e[i].v) e[i].knd=2;
		else
		{
			int now=e[i].v;
			for(int j=20;j>=0;--j)
			if(dep[fa[now][j]]>=dep[e[i].u]+1) now=fa[now][j];
			e[i].ex=now;e[i].knd=1;//判断带权路径的类型 同时求出第一类路径的第一个点z
		} 
	}
	sort(res+1,res+m+1);tot=unique(res+1,res+m+1)-res-1;
	for(int i=1;i<=m;++i)
	{//离散化 同时使用vector记录每一个权值对应的路径 便于接下来的整体二分
		e[i].w=lower_bound(res+1,res+tot+1,e[i].w)-res;
		G[e[i].w].push_back(i);
	}
	for(int i=1;i<=q;++i)
	{
		scanf("%d%d%d",&que[i].u,&que[i].v,&que[i].k);
		if(dfn[que[i].u]>dfn[que[i].v]) swap(que[i].u,que[i].v);
		que[i].id=i;
	}
	solve(1,tot,1,q);
	sort(que+1,que+q+1);
	for(int i=1;i<=q;++i) printf("%d\n",res[que[i].ans]);
	return 0;
}