学习笔记 最大闭合权子图
写在之前
最近又开始更新博客了 所以就学习了一些之前没有学过的东西
正式开始
什么是最大权闭合子图?
首先 我们需要明白 什么是闭合子图
首先 子图我们很好明白
至于闭合子图 就是子图中所有的点 他们的出度指向的点也在这个子图中
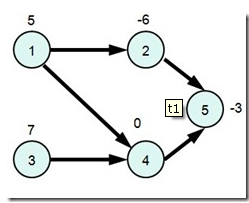
我们来一个DAG网上找的 上图理解一下
在这幅图中 {1,2,3,4},{4.5},{2,4,5}都是闭合子图
但是 {1,2,5}就不是 因为点1一个出度指向的点4不在这幅子图当中
这就是闭合子图的概念
如果加上点权的话 那么所有闭合子图当中点权和最大的就是最大权闭合子图
怎么求最大权闭合子图?
求解方式:最大流最小割
首先我们建立符合最大流的图
建立一个超级源s 和一个超级汇t
然后所有的正权点都和s相连 容量为其点权
所有的负权点都和t相连 容量为其点权的绝对值
然后 再按照原图的关系连边 容量为无穷大
然后够我们跑最小割 也就是最大流就可以了
为什么这样子建图?
请注意 我们现在跑的是最小割
所以 一个点的出度的点之间的边由于容量是无穷大 所以不可能被割掉
这也就是保证了闭合子图的成立
所以 我们只会割掉 s与正点权的点之间的边 以及负点权的点与t之间的边
最后的图就被我们分为了两部分 在最大权闭合子图里的和不在最大权闭合子图里的
最后 我们的答案 正点权的点权和 - 最小割 = 正点权的点权和 - (不在最大闭合子图正点权点权和 + 在最大权闭合子图里的负点权绝对值和) = 在最大闭合子图正点权点权和 - 在最大权闭合子图里的负点权绝对值和
这就是我们要的答案
现在 我们可以上题了