二叉树篇
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return sortedArrayToBST(nums, 0, nums.length);
}
public TreeNode sortedArrayToBST(int[] nums, int left, int right) {
if (left >= right) {
return null;
}
if (right - left == 1) {
return new TreeNode(nums[left]);
}
int mid = left + (right - left) / 2;
TreeNode root = new TreeNode(nums[mid]);
root.left = sortedArrayToBST(nums, left, mid);
root.right = sortedArrayToBST(nums, mid + 1, right);
return root;
}
}
二叉树篇
二叉树的遍历方式
前序遍历

递归
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<Integer>();
preorder(root, result);
return result;
}
public void preorder(TreeNode root, List<Integer> result) {
if (root == null) {
return;
}
result.add(root.val);
preorder(root.left, result);
preorder(root.right, result);
}
}
迭代(非递归)
/**
* 前序遍历顺序:中-左-右,入栈顺序:中-右-左
*/
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
result.add(node.val);
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
return result;
}
}
后序遍历
递归
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<postteger>();
postorder(root, result);
return result;
}
public void postorder(TreeNode root, List<Integer> result) {
if (root == null) {
return;
}
// 后序:左右根
postorder(root.left, result);
postorder(root.right, result);
result.add(root.val);
}
}
迭代(非递归)
/**
* 后序遍历顺序 左-右-中 入栈顺序:中-左-右 出栈顺序:中-右-左, 最后翻转结果
*/
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
result.add(node.val);
if (node.left != null) {
stack.push(node.left);
}
if (node.right != null) {
stack.push(node.right);
}
}
// 这个地方翻转很重要
Collections.reverse(result);
return result;
}
}
这个地方,后序是左右根,我们先得到根右左,然后再进行翻转,然后根右左,可以通过和先序一样的方法得到。
中序遍历

递归
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<Integer>();
inorder(root, result);
return result;
}
public void inorder(TreeNode root, List<Integer> result) {
if (root == null) {
return;
}
// 中序:左根右
inorder(root.left, result);
result.add(root.val);
inorder(root.right, result);
}
}
迭代(非递归)
/**
* 中序遍历顺序: 左-中-右 入栈顺序: 左-右
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
if (cur != null) {
stack.push(cur);
// 处理左节点
cur = cur.left;
} else {
// 最左节点取出来并加入数组
cur = stack.pop();
result.add(cur.val);
// 处理右节点
cur = cur.right;
}
}
return result;
}
}
二叉树统一迭代法
以前序为例:
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
if (node.right != null) {
st.push(node.right); // 添加右节点(空节点不入栈)
}
if (node.left != null) {
st.push(node.left); // 添加左节点(空节点不入栈)
}
st.push(node);
st.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
st.pop(); // 将空节点弹出
node = st.peek(); // 重新取出栈中元素
st.pop();
result.add(node.val); // 加入到结果集
}
}
return result;
}
}
这个做法,以前序为例,根左右。先访问根,再删除根,通过根的记录找到右子树和左子树,最后再重新访问根,达到右左根的顺序,放入栈中,出栈访问的顺序即为根左右。
层序遍历
自顶向下的层序遍历
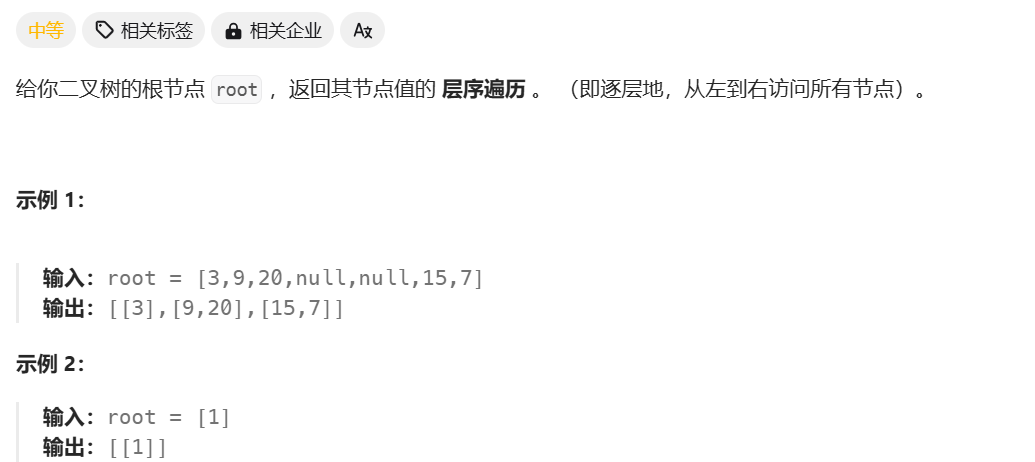
法二 递归
/**
* BFS--递归方式
*/
class Solution {
public List<List<Integer>> resList = new ArrayList<List<Integer>>();
public List<List<Integer>> levelOrder(TreeNode root) {
checkFun01(root, 0);
return resList;
}
// BFS --递归方式
public void checkFun01(TreeNode node, Integer deep) {
if (node == null) return;
deep++;
// 到达新的一层时,先创建新一层的集合
if (resList.size() < deep) {
//当层级增加时,list的Item也增加,利用list的索引值进行层级界定
List<Integer> item = new ArrayList<Integer>();
resList.add(item);
}
resList.get(deep-1).add(node.val);
checkFun01(node.left, deep);
checkFun01(node.right, deep);
}
}
我经常使用的方法-法一
/**
* BFS--迭代方式--借助队列
*/
class Solution {
public List<List<Integer>> resList = new ArrayList<List<Integer>>();
public List<List<Integer>> levelOrder(TreeNode root) {
checkFun02(root);
return resList;
}
// BFS--迭代方式--借助队列
public void checkFun02(TreeNode node) {
if (node == null) return;
Queue<TreeNode> que = new LinkedList<TreeNode>();
que.offer(node);
while (!que.isEmpty()) {
List<Integer> itemList = new ArrayList<Integer>();
int len = que.size();
while (len > 0) {
TreeNode tmpNode = que.poll();
itemList.add(tmpNode.val);
if (tmpNode.left != null) que.offer(tmpNode.left);
if (tmpNode.right != null) que.offer(tmpNode.right);
len--;
}
resList.add(itemList);
}
}
}
自底向上的层序遍历
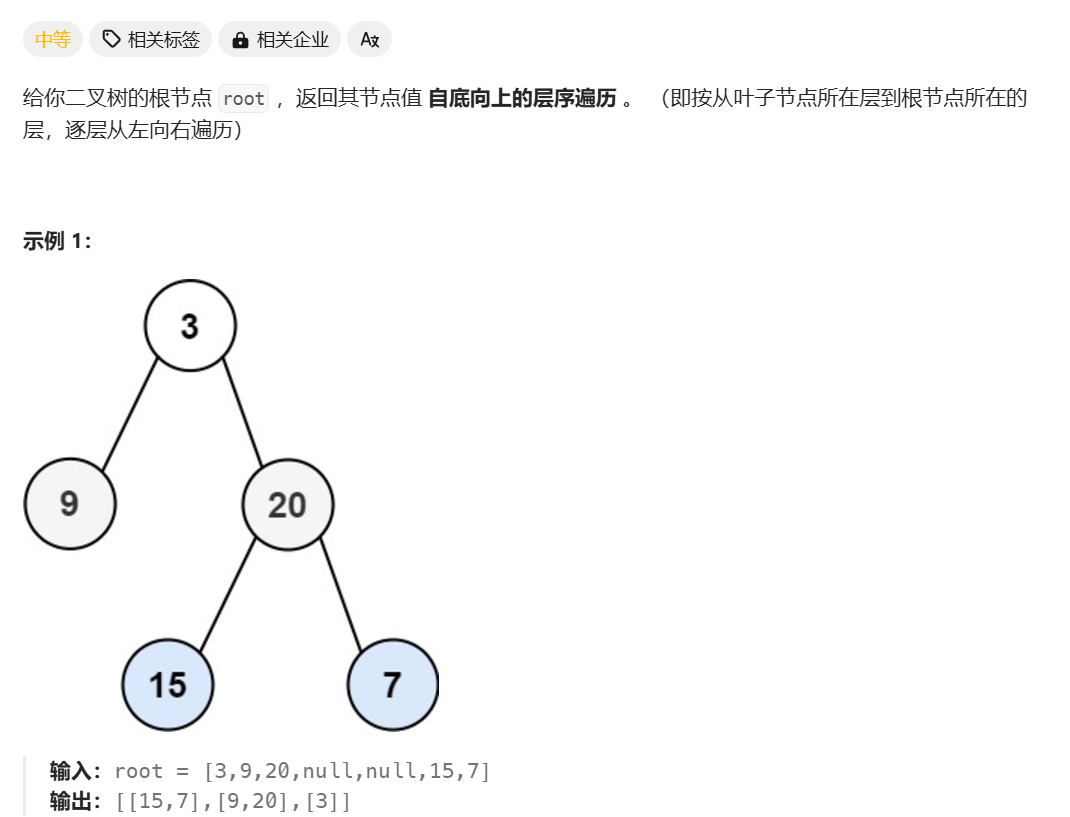
相当于自顶向上的层序遍历,然后将数组里面的小数组从新换个顺序即可
List<List<Integer>> result = new ArrayList<>();
for (int i = list.size() - 1; i >= 0; i-- ) {
result.add(list.get(i));
}
二叉树的属性
对称二叉树
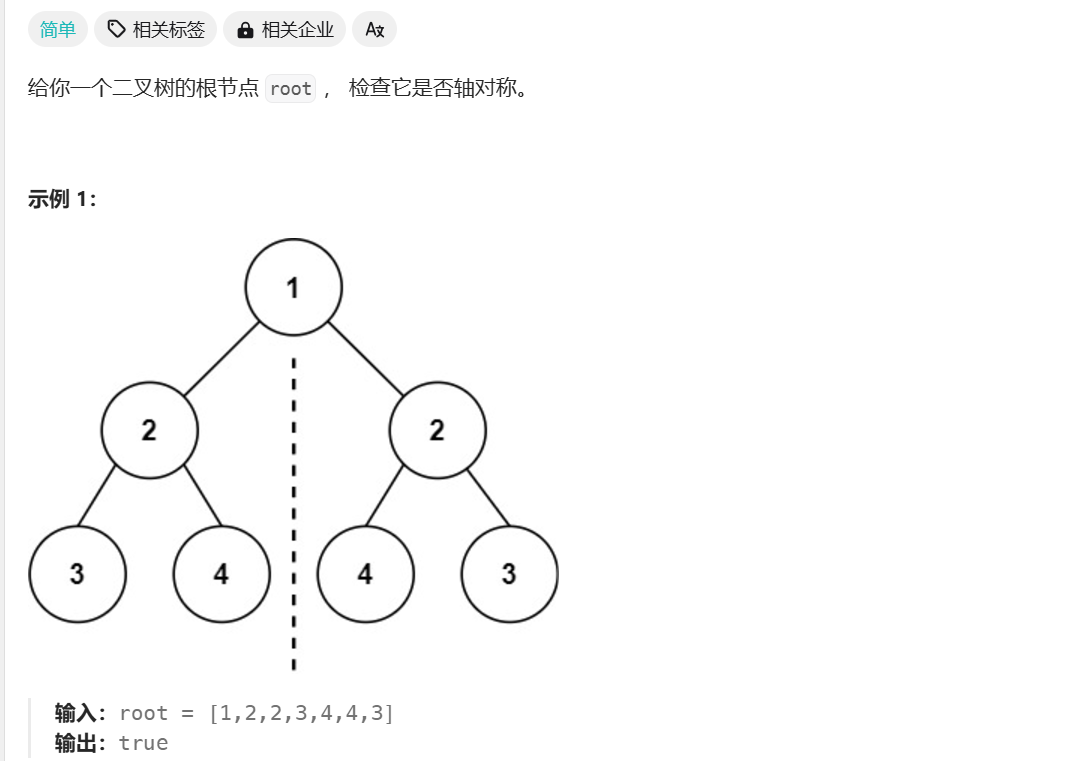
/**
* 递归法
*/
class Solution {
public boolean isSymmetric(TreeNode root) {
return compare(root.left, root.right);
}
private boolean compare(TreeNode left, TreeNode right) {
if (left == null && right != null) {
return false;
}
if (left != null && right == null) {
return false;
}
if (left == null && right == null) {
return true;
}
if (left.val != right.val) {
return false;
}
// 比较外侧
boolean compareOutside = compare(left.left, right.right);
// 比较内侧
boolean compareInside = compare(left.right, right.left);
return compareOutside && compareInside;
}
}
二叉树的最大深度
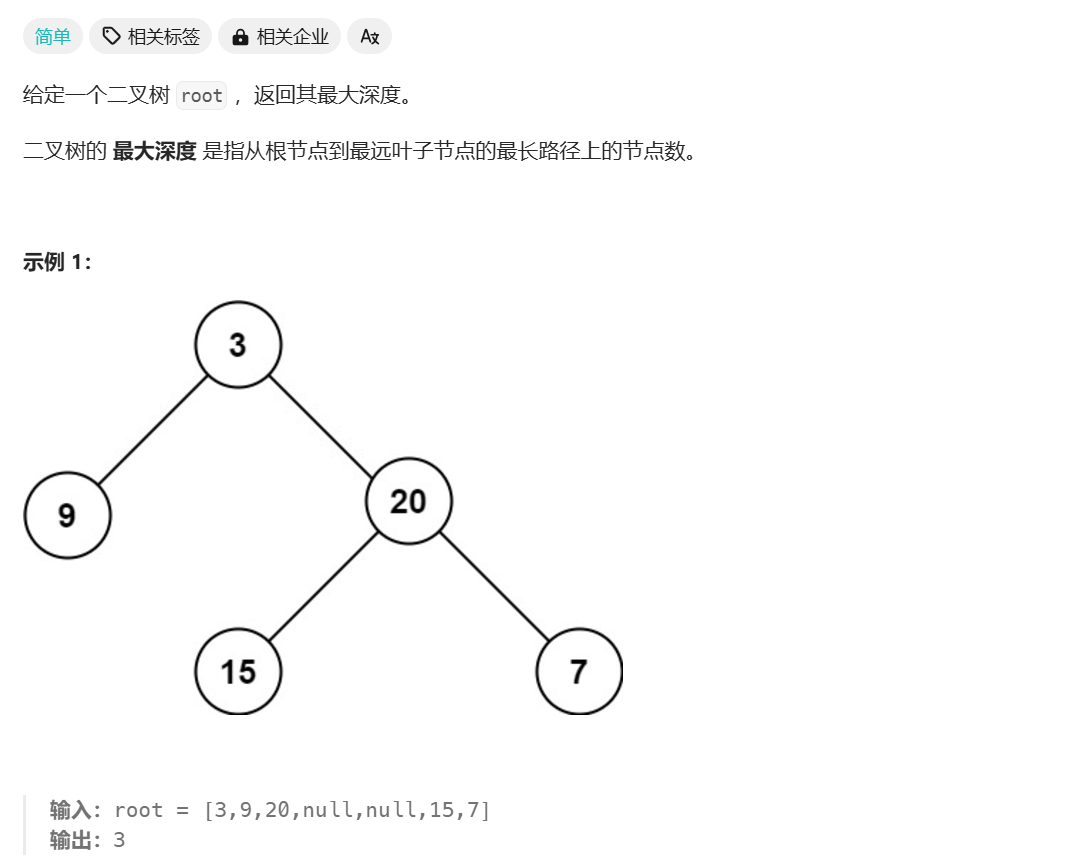
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) return 0;
Queue<TreeNode> que = new LinkedList<>();
que.offer(root);
int depth = 0;
while (!que.isEmpty()) {
int len = que.size();
// 这个地方一直在处理某一层的所有元素
while (len > 0) {
TreeNode node = que.poll();
if (node.left != null) que.offer(node.left);
if (node.right != null) que.offer(node.right);
len--;
}
depth++;
}
return depth;
}
}
二叉树的最小深度
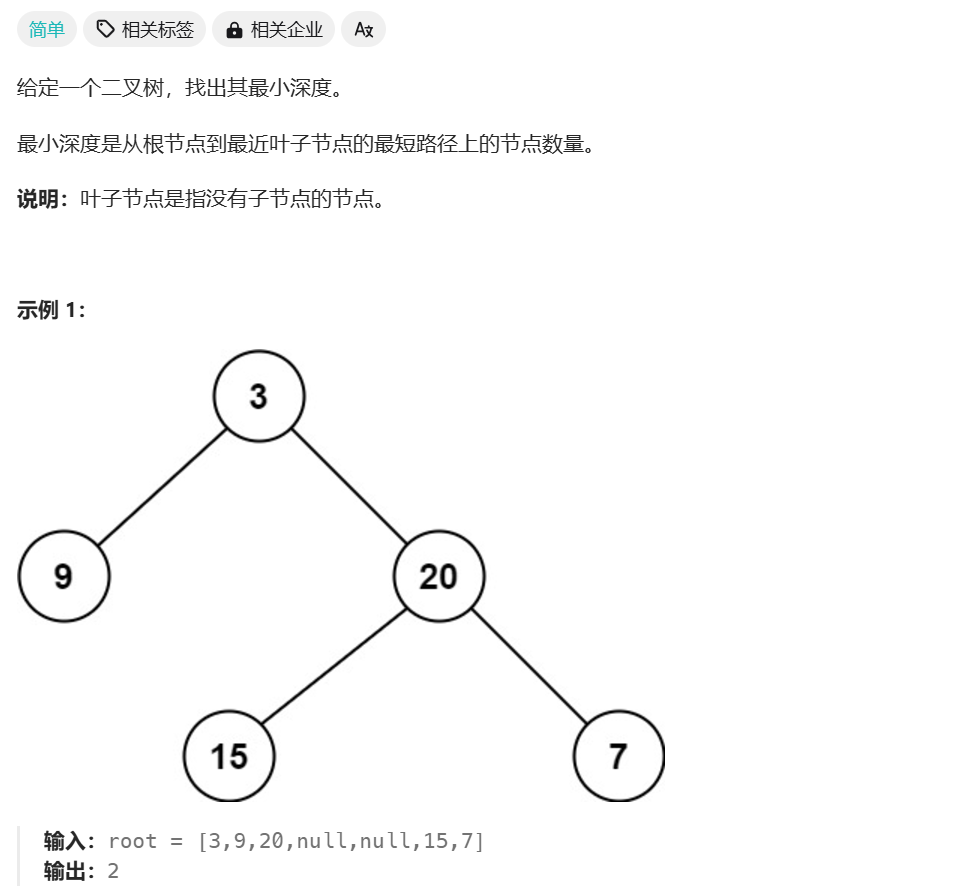
我自己编写的代码
我自己编写的代码,和答案的思路差不多
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int minDepth(TreeNode root) {
if (root == null) return 0;
Queue<TreeNode> que = new LinkedList<>();
que.offer(root);
int depth = 0;
while (!que.isEmpty()) {
int len = que.size();
// 这个地方一直在处理某一层的所有元素
TreeNode node;
while (len > 0) {
node = que.poll();
if (node.left != null) que.offer(node.left);
if (node.right != null) que.offer(node.right);
len--;
// 下面这个地方是我自己加的,只要找到左右子树为空的,说明就到这了
if (node.left == null && node.right == null) {
depth++;
return depth;
}
}
depth++;
}
return depth;
}
}
根据答案修改了一下细节
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int minDepth(TreeNode root) {
if (root == null) return 0;
Queue<TreeNode> que = new LinkedList<>();
que.offer(root);
int depth = 0;
while (!que.isEmpty()) {
int len = que.size();
// 这个地方一直在处理某一层的所有元素
depth++;
while (len > 0) {
TreeNode node = que.poll();
// 下面这个地方是我自己加的,只要找到左右子树为空的,说明就到这了
if (node.left == null && node.right == null) {
return depth;
}
if (node.left != null) que.offer(node.left);
if (node.right != null) que.offer(node.right);
len--;
}
}
return depth;
}
}
完全二叉树的节点个数
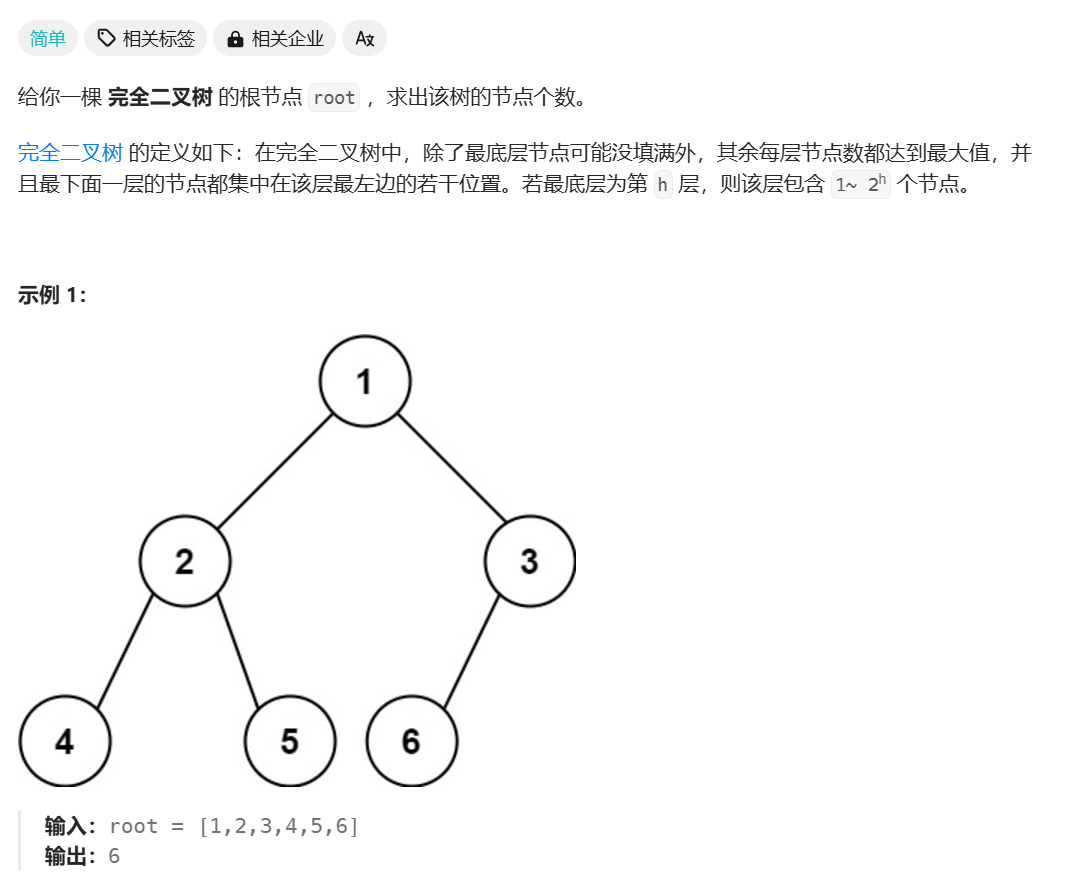
递归解法
/**
* 通用递归解法
*/
class Solution {
public int countNodes(TreeNode root) {
if (root == null) return 0;
return countNodes(root.left) + countNodes(root.right) + 1;
}
}
完全二叉树解法
/**
* 针对完全二叉树的解法
* 满二叉树的结点数为:2^depth - 1
*/
class Solution {
public int countNodes(TreeNode root) {
if (root == null) return 0;
TreeNode left = root.left;
TreeNode right = root.right;
int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的,为了下面求指数方便
while (left != null) { // 求左子树深度
left = left.left;
leftDepth++;
}
while (right != null) { // 求右子树深度
right = right.right;
rightDepth++;
}
if (leftDepth == rightDepth) {
return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2,所以leftDepth初始为0
}
return countNodes(root.left) + countNodes(root.right) + 1;
}
}
平衡二叉树
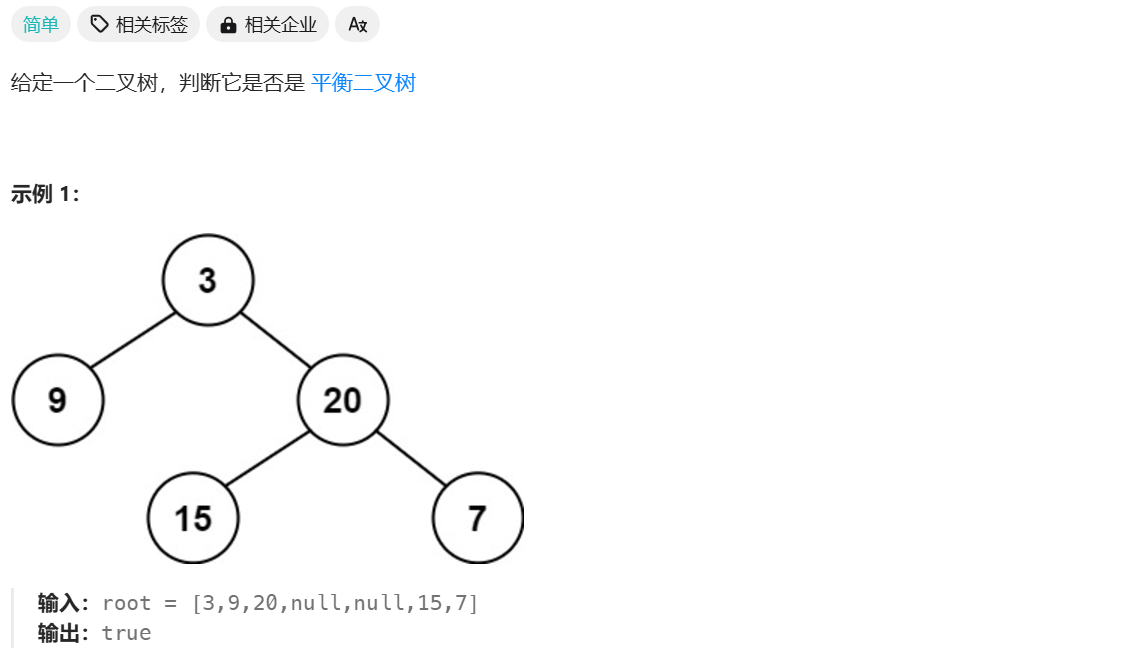
/**
* 递归法
*/
class Solution {
public boolean isBalanced(TreeNode root) {
return getHeight(root) != -1;
}
private int getHeight(TreeNode root) {
// 如果发现不是平衡的二叉树,则会直接返回-1
if (root == null) return 0;
int leftHeight = getHeight(root.left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(root.right);
if (rightHeight == -1) return -1;
// 左右子树高度差大于1,return -1表示已经不是平衡树了
if (Math.abs(leftHeight - rightHeight) > 1) return -1;
return Math.max(leftHeight, rightHeight) + 1;
}
}
二叉树的所有路径
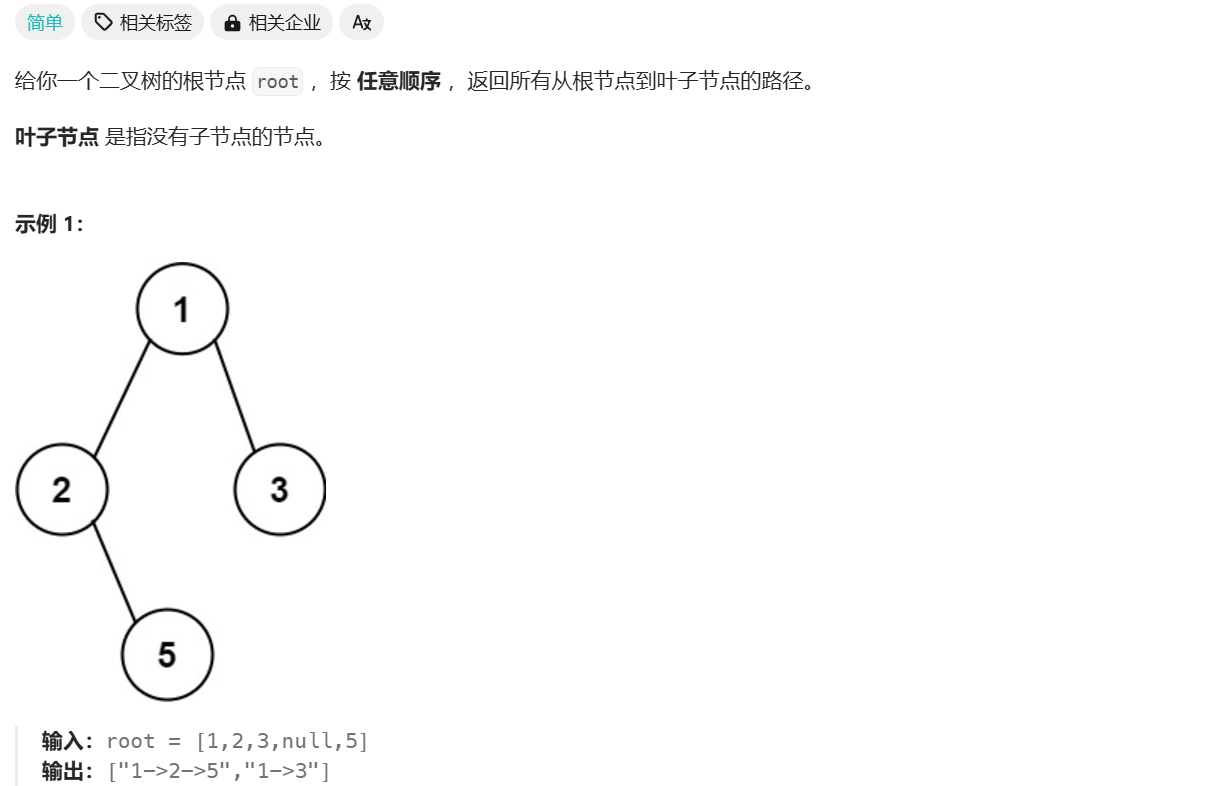
/**
* 递归法
*/
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> res = new ArrayList<>(); // 存最终的结果
if (root == null) return res;
List<Integer> paths = new ArrayList<>(); // 作为结果中的路径
traversal(root, paths, res);
return res;
}
private void traversal(TreeNode root, List<Integer> paths, List<String> res) {
paths.add(root.val); // 前序遍历: 根
// 遇到叶子结点
if (root.left == null && root.right == null) {
// 输出
StringBuilder sb = new StringBuilder(); // StringBuilder用来拼接字符串,速度更快
for (int i=0; i<paths.size()-1; i++) {
sb.append(paths.get(i)).append("->");
}
sb.append(paths.get(paths.size()-1)); // 记录最后一个节点
res.add(sb.toString()); // 收集一个路径
return;
}
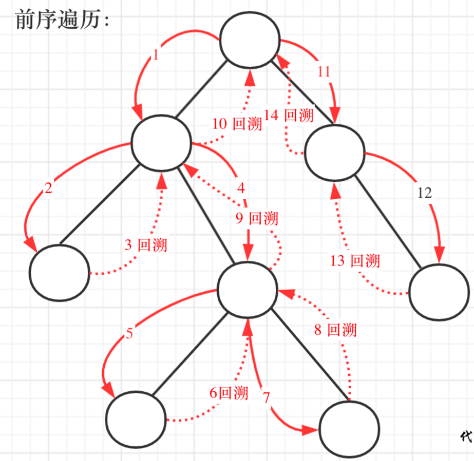
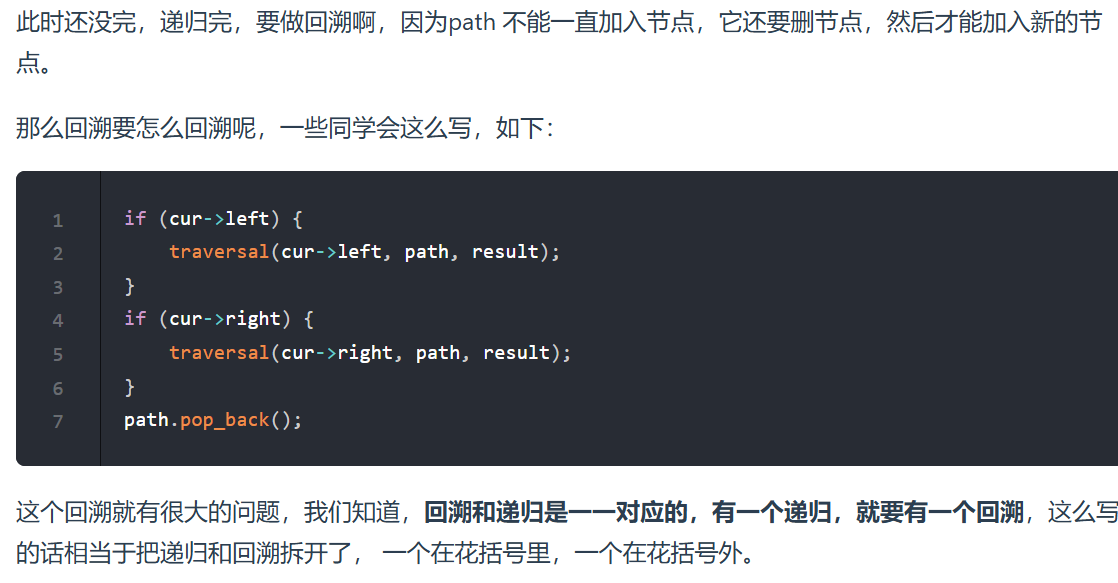
// 递归和回溯是同时进行,所以要放在同一个花括号里
if (root.left != null) {
traversal(root.left, paths, res);
paths.remove(paths.size()-1); // 回溯
}
if (root.right != null) { // 右
traversal(root.right, paths, res);
paths.remove(paths.size() - 1);// 回溯
}
}
}
这个代码目前有回溯的内容了,所以理解起来感觉还是有一点困难的。
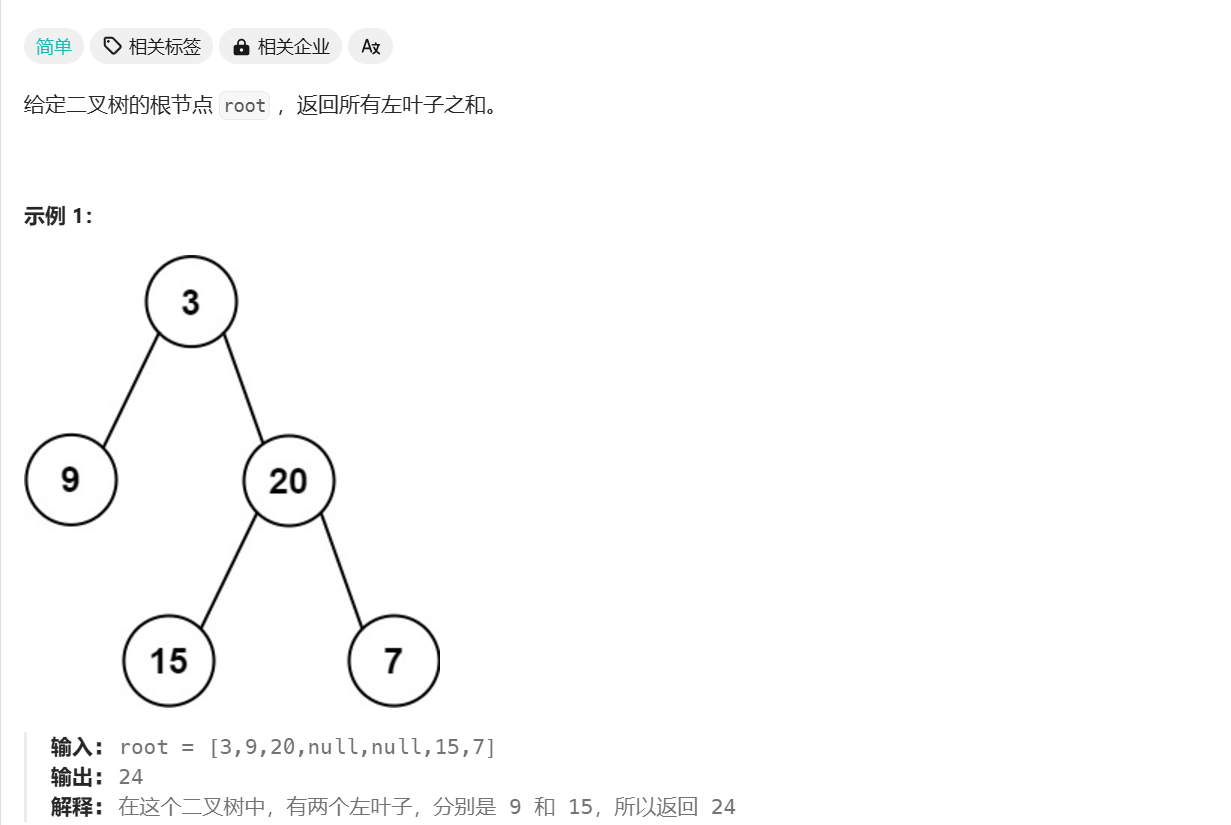
左叶子之和
/**
* 递归求解
*/
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
if (root == null) return 0;
int leftValue = sumOfLeftLeaves(root.left);
int rightValue = sumOfLeftLeaves(root.right);
int midValue = 0;
// 对于当前根节点,判断其左孩子节点是否是叶子节点
if (root.left != null && root.left.left == null && root.left.right == null) {
midValue = root.left.val;
}
int sum = midValue + leftValue + rightValue;
return sum;
}
}
找树左下角的值
题目的含义是:找最底层当中所有元素的第一个(由左到右)

/**
* 递归法
* 使用前序遍历,这样才先优先左边搜索,然后记录深度最大的叶子节点,此时就是树的最后一行最左边的值。
*/
class Solution {
private int Deep = -1;
private int value = 0;
public int findBottomLeftValue(TreeNode root) {
value = root.val;
findLeftValue(root, 0);
return value;
}
private void findLeftValue(TreeNode root, int deep) {
if (root == null) return;
if (root.left == null && root.right == null) {
if (deep > Deep) {
value = root.val;
Deep = deep;
}
}
if (root.left != null) findLeftValue(root.left, deep+1);
if (root.right != null) findLeftValue(root.right, deep+1);
}
}
/**
* 迭代法
*/
class Solution {
public int findBottomLeftValue(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int res = 0;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i=0;i<size;i++) {
TreeNode poll = queue.poll();
if (i == 0) {
res = poll.val; // 最先保留左边的值
}
if (poll.left != null) {
queue.offer(poll.left);
}
if (poll.right != null) {
queue.offer(poll.right);
}
}
}
return res;
}
}
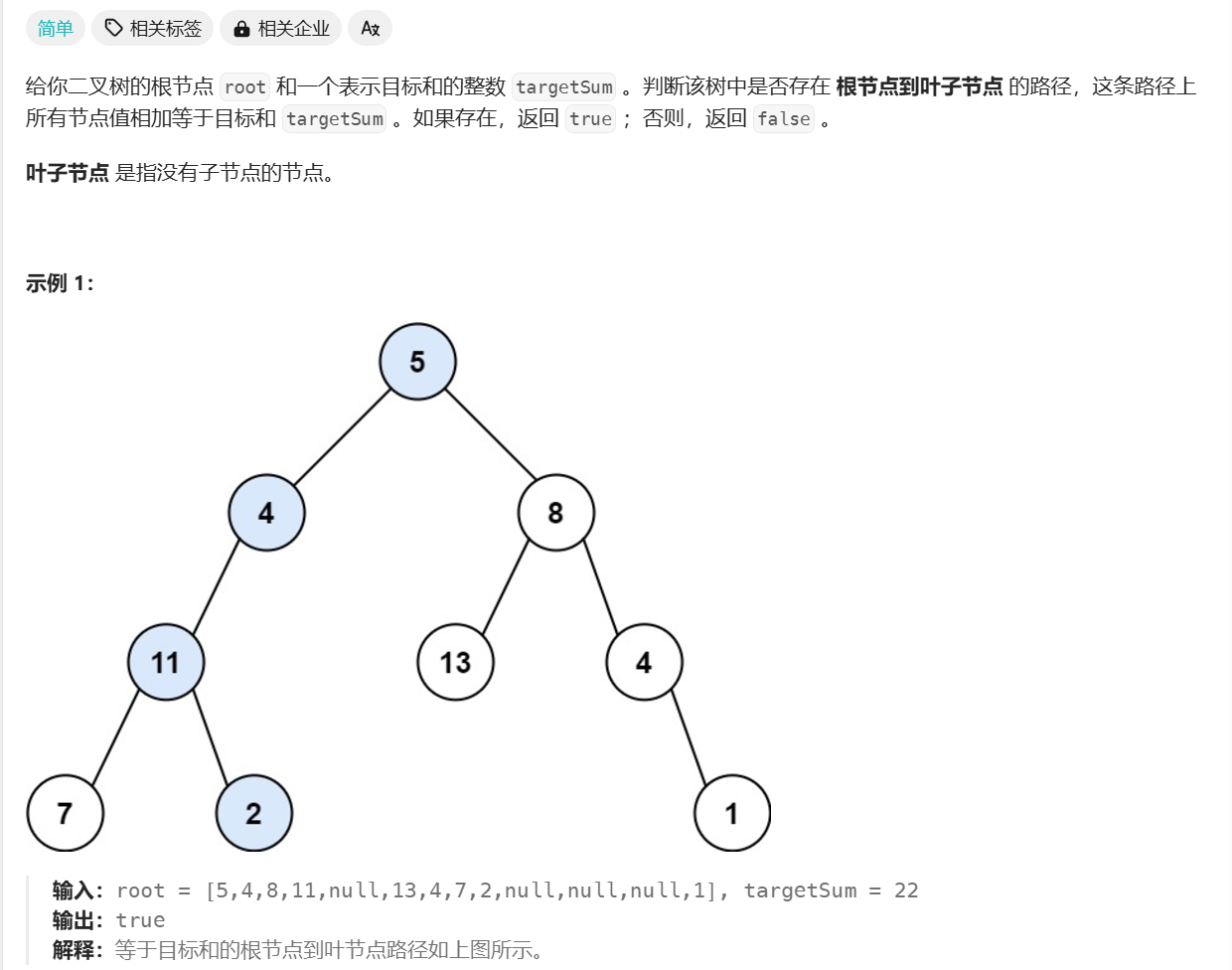
路径总和
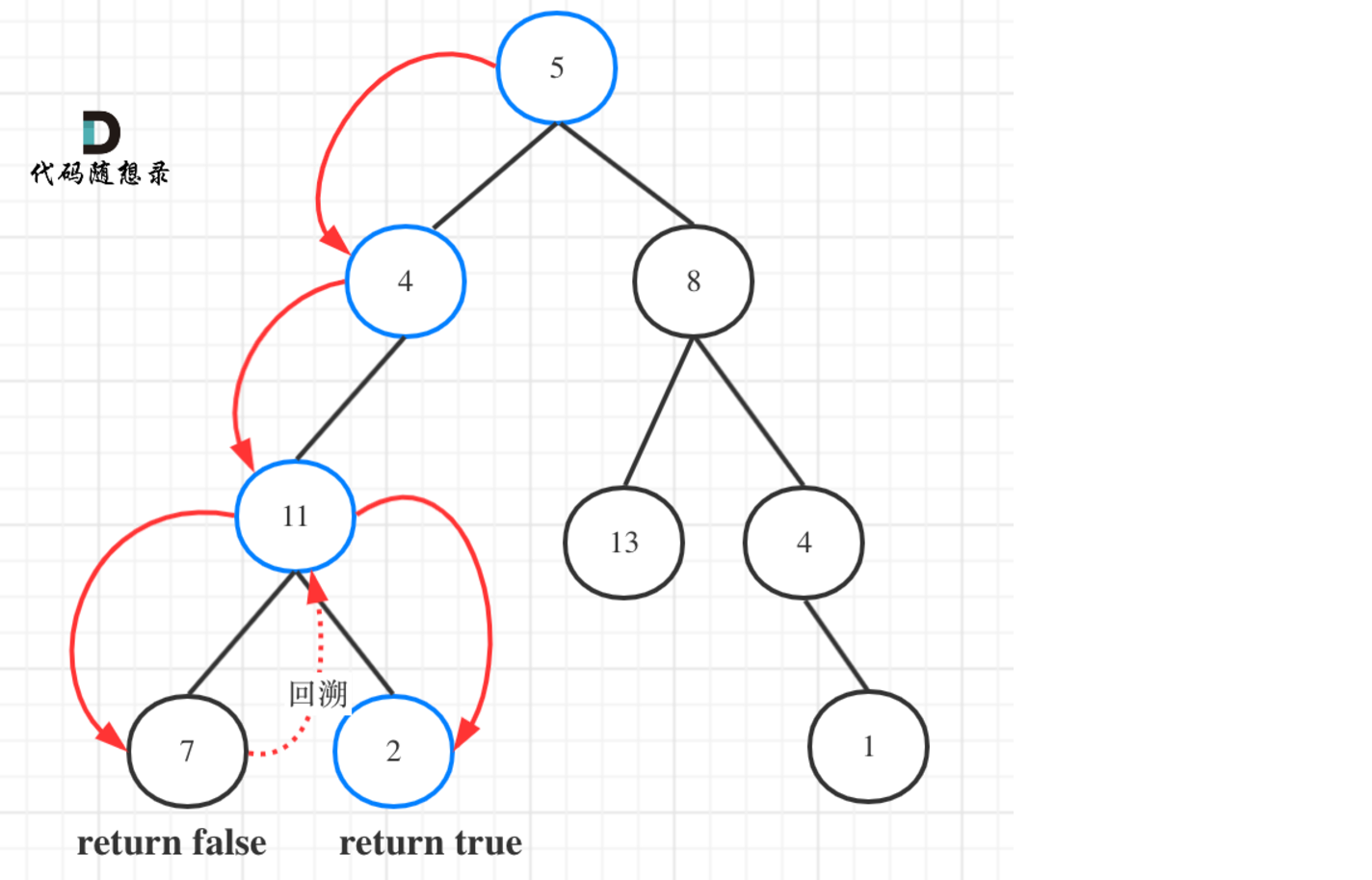
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null) return false;
targetSum -= root.val;
// 叶子节点
if (root.left == null && root.right == null) {
return targetSum == 0;
}
if (root.left != null) {
boolean left = hasPathSum(root.left, targetSum);
if (left) return true; // 已经找到
}
if (root.right != null) {
boolean right = hasPathSum(root.right, targetSum);
if (right) return true;
}
return false;
}
}
二叉树的修改与构造
翻转二叉树
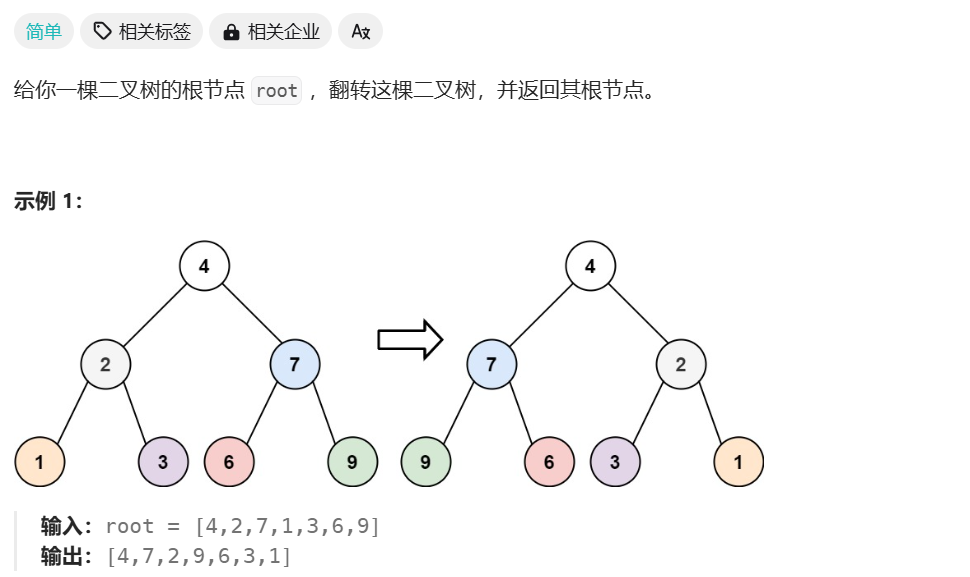
/**
* 前后序遍历都可以
* 中序不行,因为先左孩子交换孩子,再根交换孩子(做完后,右孩子已经变成了原来的左孩子),再右孩子交换孩子(此时其实是对原来的左孩子做交换)
*/
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
swapChildren(root);
invertTree(root.left);
invertTree(root.right);
return root;
}
private void swapChildren(TreeNode root) {
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
}
}
从中序与后序遍历序列构造二叉树
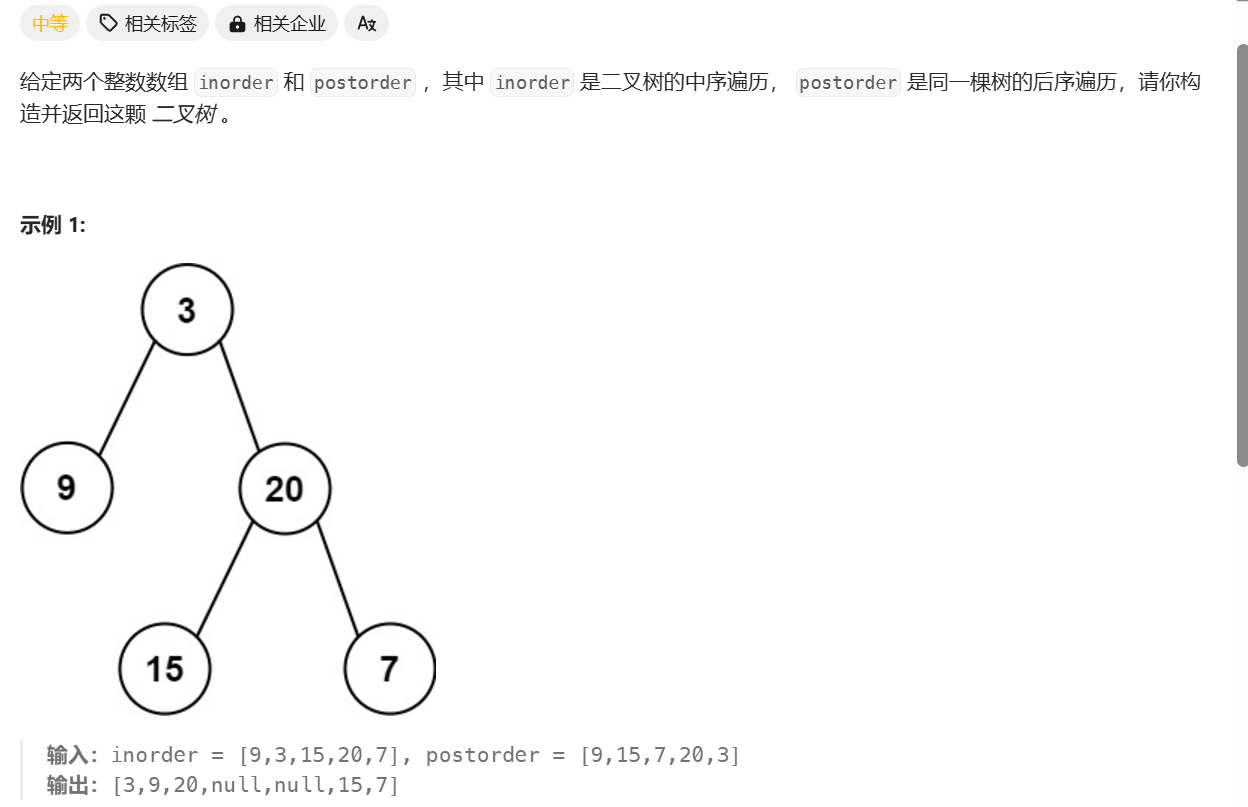
class Solution {
Map<Integer, Integer> map; // 方便根据数值查找位置
public TreeNode buildTree(int[] inorder, int[] postorder) {
map = new HashMap<>();
for (int i=0;i<inorder.length;i++) {
map.put(inorder[i], i);
}
return findNode(inorder, 0, inorder.length, postorder, 0, postorder.length);// 前闭后开
}
public TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {
// 参数里的范围都是前闭后开
if (inBegin >= inEnd || postBegin >= postEnd) {
return null; // 不满足左闭右开,说明没有元素,返回空树
}
int rootIndex = map.get(postorder[postEnd - 1]); // 找到后序遍历的最后一个元素在中序遍历中的位置
TreeNode root = new TreeNode(inorder[rootIndex]); // 构造结点
int lenOfLeft = rootIndex - inBegin; // 保存中序左子树个数,用来确定后序数列的个数
root.left = findNode(inorder, inBegin, rootIndex, postorder, postBegin, postBegin+lenOfLeft);
root.right = findNode(inorder, rootIndex+1, inEnd, postorder, postBegin+lenOfLeft, postEnd-1);
return root;
}
}
最大二叉树

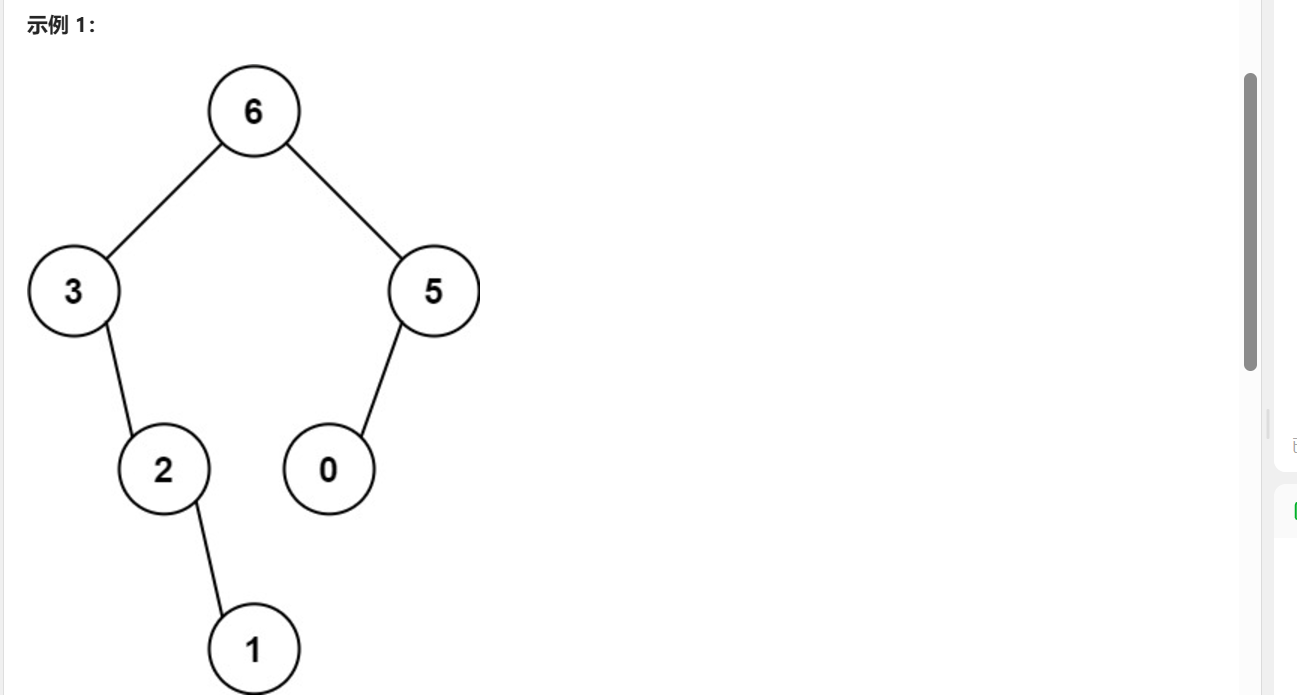

class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
return cMBT(nums, 0, nums.length);
}
public TreeNode cMBT(int[] nums, int leftIndex, int rightIndex) { // 左开右闭
if (rightIndex - leftIndex < 1) return null; // 没有元素了
if (rightIndex - leftIndex == 1) return new TreeNode(nums[leftIndex]); // 只有一个元素
int maxIndex = leftIndex; // 最大值所在位置
int maxVal = nums[maxIndex]; // 最大值
for (int i=leftIndex+1; i<rightIndex; i++) { // 找最大值
if (nums[i] > maxVal) {
maxVal = nums[i];
maxIndex = i;
}
}
TreeNode root = new TreeNode(maxVal);
// 根据maxIndex划分左右子树
root.left = cMBT(nums, leftIndex, maxIndex);
root.right = cMBT(nums, maxIndex+1, rightIndex);
return root;
}
}
合并二叉树
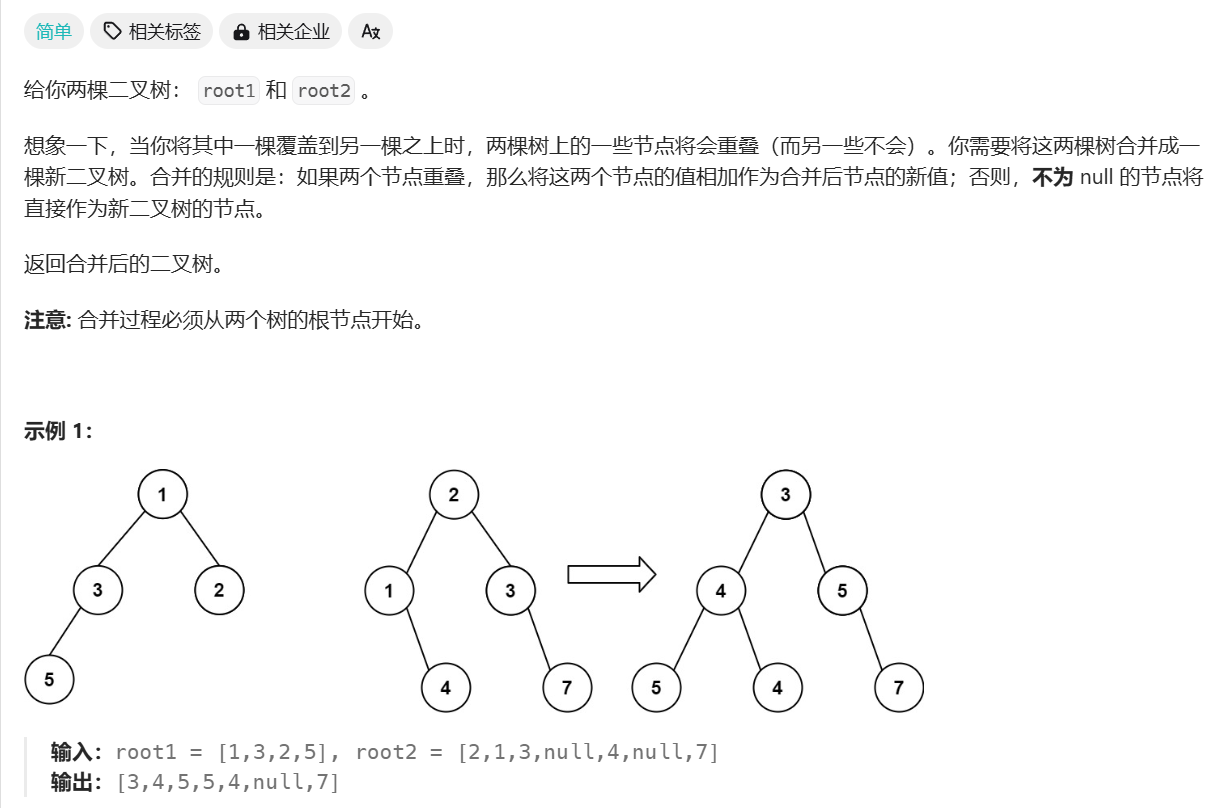
/**
* 递归法
*/
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if (root1 == null) return root2;
if (root2 == null) return root1;
root1.val += root2.val;
root1.left = mergeTrees(root1.left, root2.left);
root1.right = mergeTrees(root1.right, root2.right);
return root1;
}
}
二叉搜索树的属性
二叉搜索树中的搜索
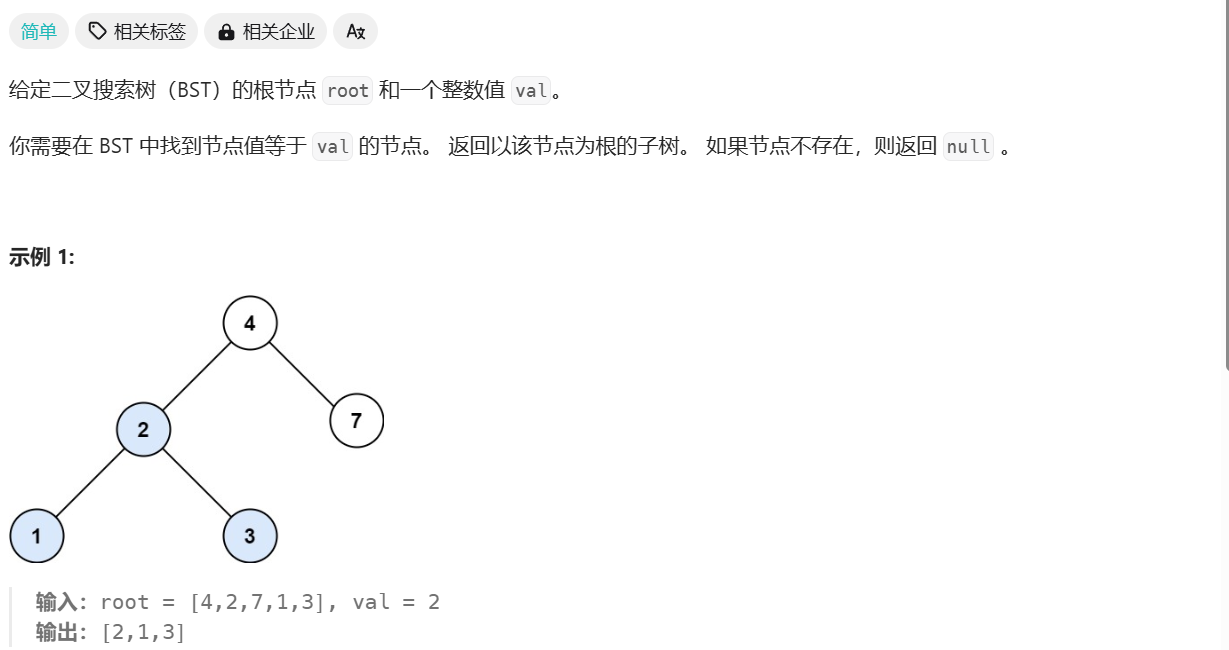
/**
* 递归,利用二叉搜索树特点,优化
*/
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
if (root == null || root.val == val) return root;
if (val < root.val) return searchBST(root.left, val);
else return searchBST(root.right, val);
}
}
做-验证二叉搜索树
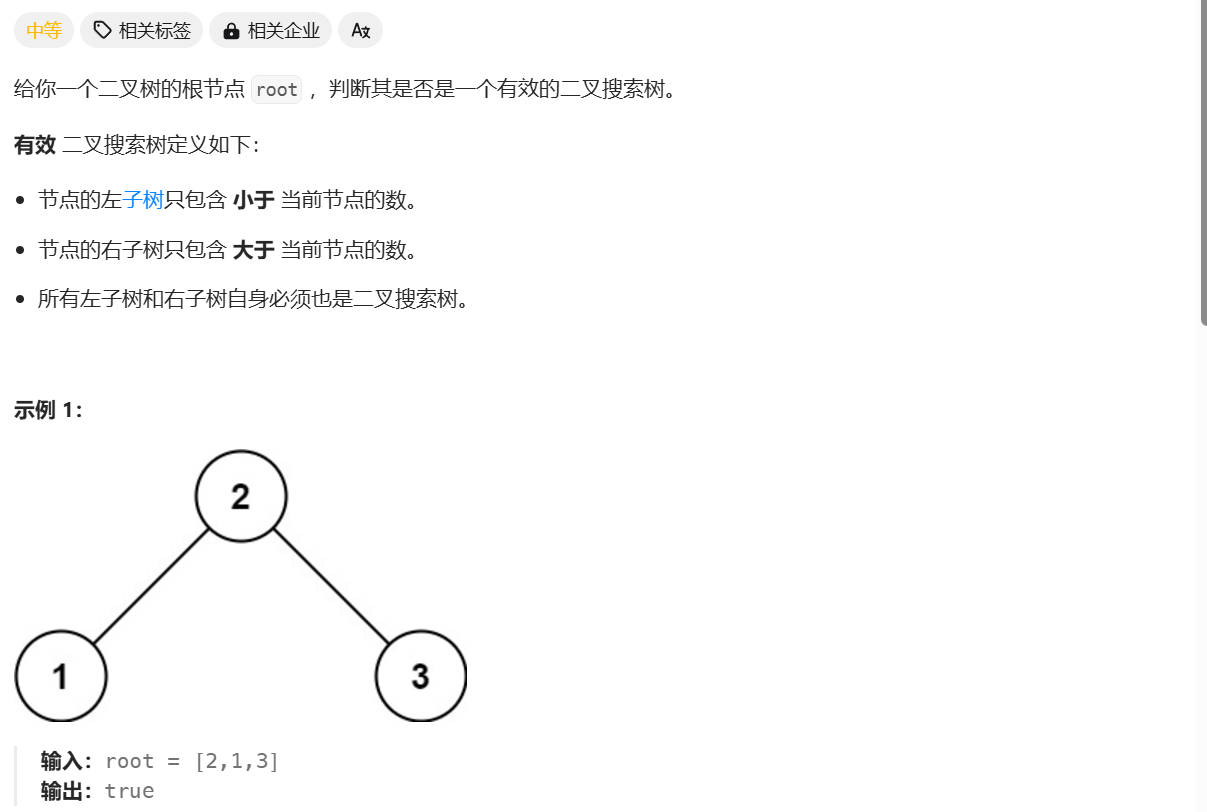
还要继续理清楚逻辑
/**
* 中序遍历实现。左 < 中 <右
* pre 记录的是当前节点的前一个节点(中序序列中当前节点的前一个)
*/
class Solution {
TreeNode pre;
public boolean isValidBST(TreeNode root) {
if (root == null) return true;
// 左子树不满足,则返回
boolean left = isValidBST(root.left);
if (!left) return false;
// 根和前一个比较
if (pre != null && root.val <= pre.val) {
return false;
}
pre = root;
// 右子树不满足,则返回
boolean right = isValidBST(root.right);
return right;
}
}

二叉搜索树的最小绝对差
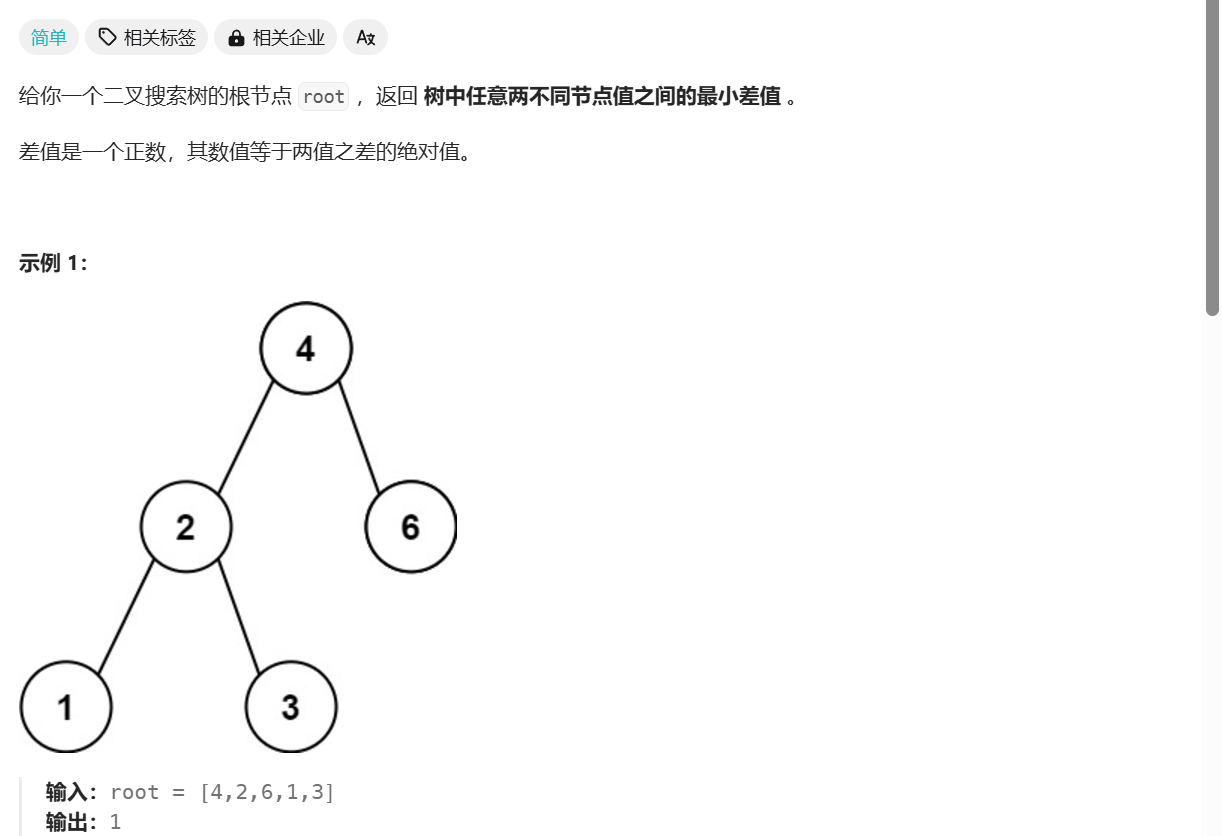
/**
* 中序遍历实现。左 < 中 <右
* pre 记录的是当前节点的前一个节点(中序序列中当前节点的前一个)
*/
class Solution {
TreeNode pre; // 记录上一个遍历的结点
int result = Integer.MAX_VALUE;
public int getMinimumDifference(TreeNode root) {
if (root == null) return 0;
traversal(root);
return result;
}
public void traversal(TreeNode root) {
if (root == null) return;
// 左
traversal(root.left);
// 根
if (pre != null) {
result = Math.min(result, root.val - pre.val);
}
pre = root;
// 右
traversal(root.right);
}
}

二叉搜索树中的众数

class Solution {
ArrayList<Integer> resList;
int maxCount;
int count;
TreeNode pre;
public int[] findMode(TreeNode root) {
resList = new ArrayList<>();
maxCount = 0;
count = 0;
pre = null; // 初始化前一个为null
findMode1(root);
int[] res = new int[resList.size()];
for (int i=0; i<resList.size(); i++) {
res[i] = resList.get(i);
}
return res;
}
public void findMode1(TreeNode root) {
if (root == null) return;
// 左
findMode1(root.left);
int rootValue = root.val;
// 计数
if (pre == null || rootValue != pre.val) {
count = 1;
} else {
count++;
}
// 更新结果以及maxCount
if (count > maxCount) {
resList.clear();
resList.add(rootValue);
maxCount = count;
} else if (count == maxCount) {
resList.add(rootValue);
}
pre = root;
// 右
findMode1(root.right);
}
}
理解清楚里面的逻辑。还是利用二叉搜索树的中序序列递增的特点。
把二叉搜索树转换为累加树

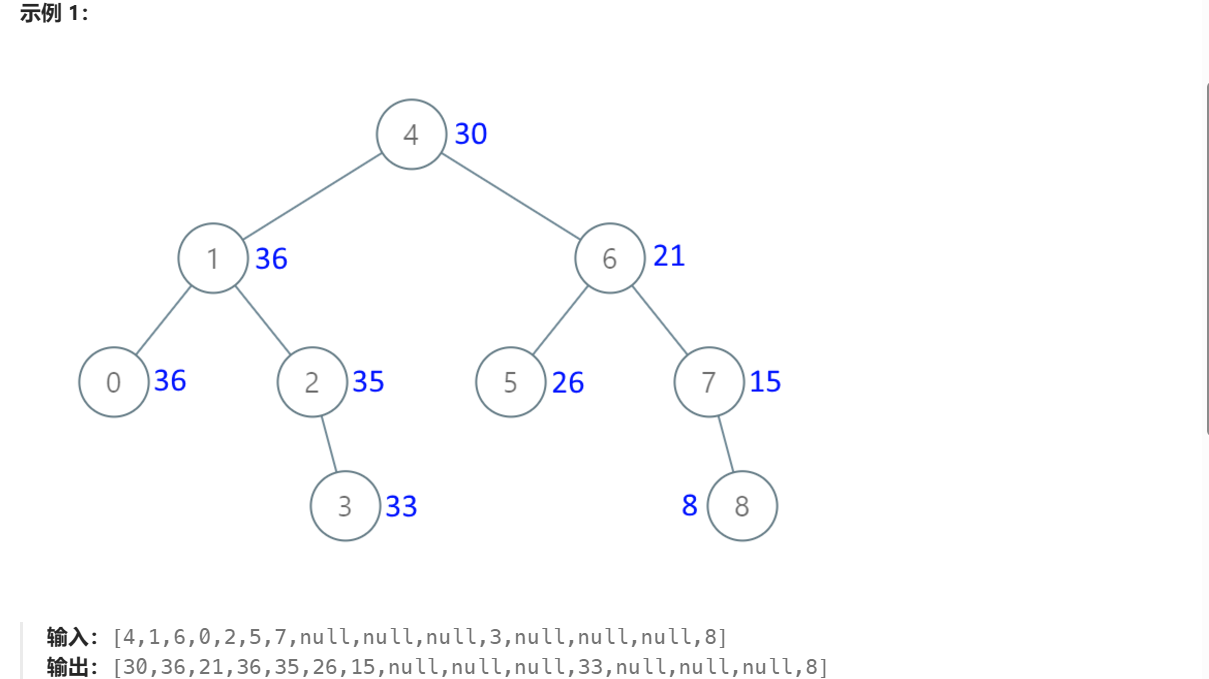
class Solution {
int sum;
public TreeNode convertBST(TreeNode root) {
sum = 0;
convertBST1(root);
return root;
}
// 按右中左顺序遍历,累加即可
public void convertBST1(TreeNode root) {
if (root == null) return;
// 右
convertBST1(root.right);
sum += root.val;
root.val = sum;
// 左
convertBST1(root.left);
}
}
二叉树公共祖先问题
做-二叉树的最近公共祖先

class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root==null || root==p || root==q) { // 递归结束条件
return root;
}
// 后序遍历
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left==null && right==null) { // 若未找到节点 p 或 q
return null;
} else if (left==null && right!=null) { // 若找到一个节点
return right;
} else if (left!=null && right==null) { // 若找到一个节点
return left;
} else { // 若找到两个节点
return root;
}
}
}


二叉搜索树的最近公共祖先

class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root.val > p.val && root.val > q.val) {
return lowestCommonAncestor(root.left, p, q);
}
if (root.val < p.val && root.val < q.val) {
return lowestCommonAncestor(root.right, p, q);
}
return root;
}
}

下面这两幅图就是例子:理解上面的递归代码的含义
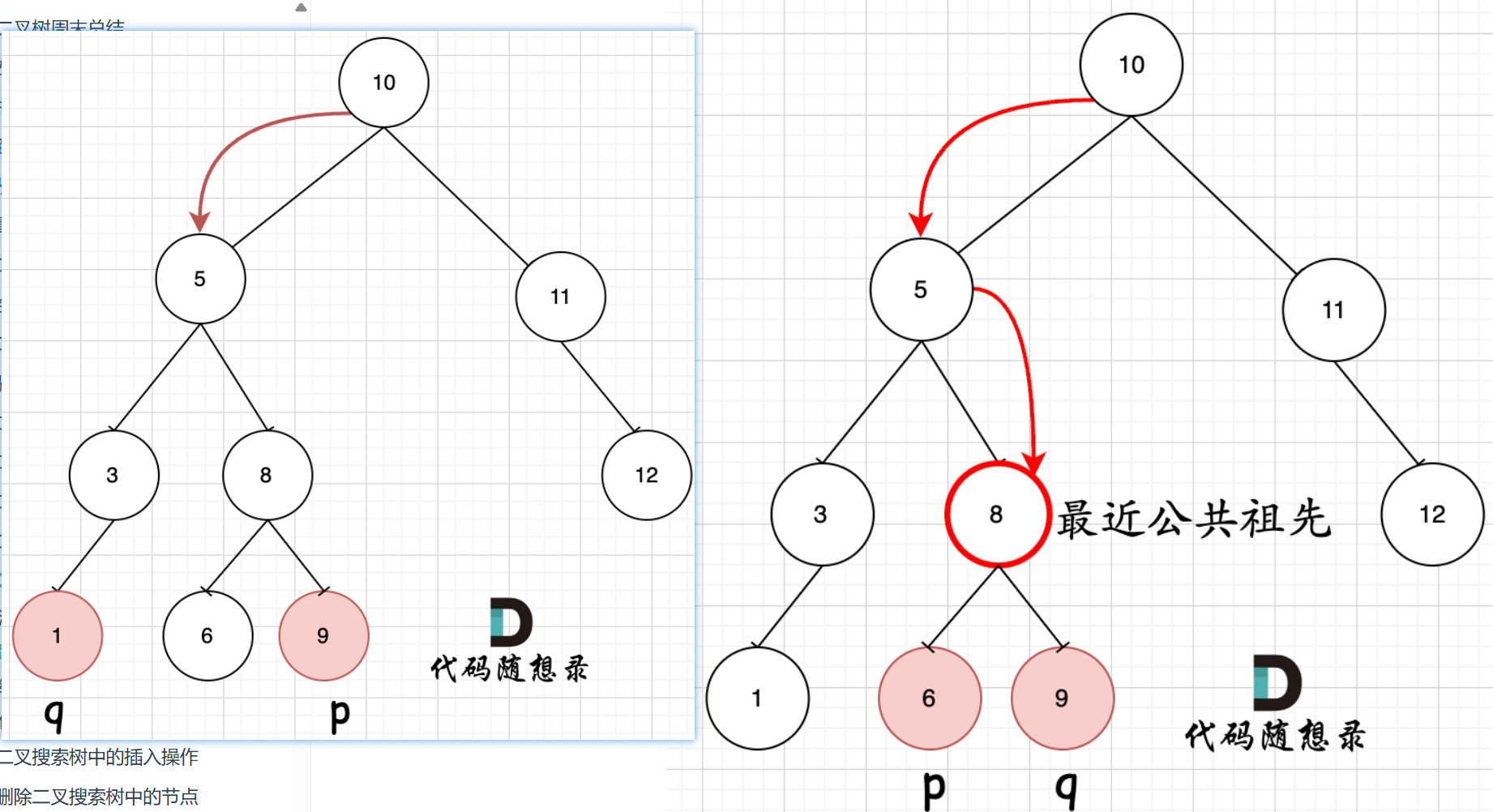
二叉搜索树的修改与构造
二叉搜索树的插入操作
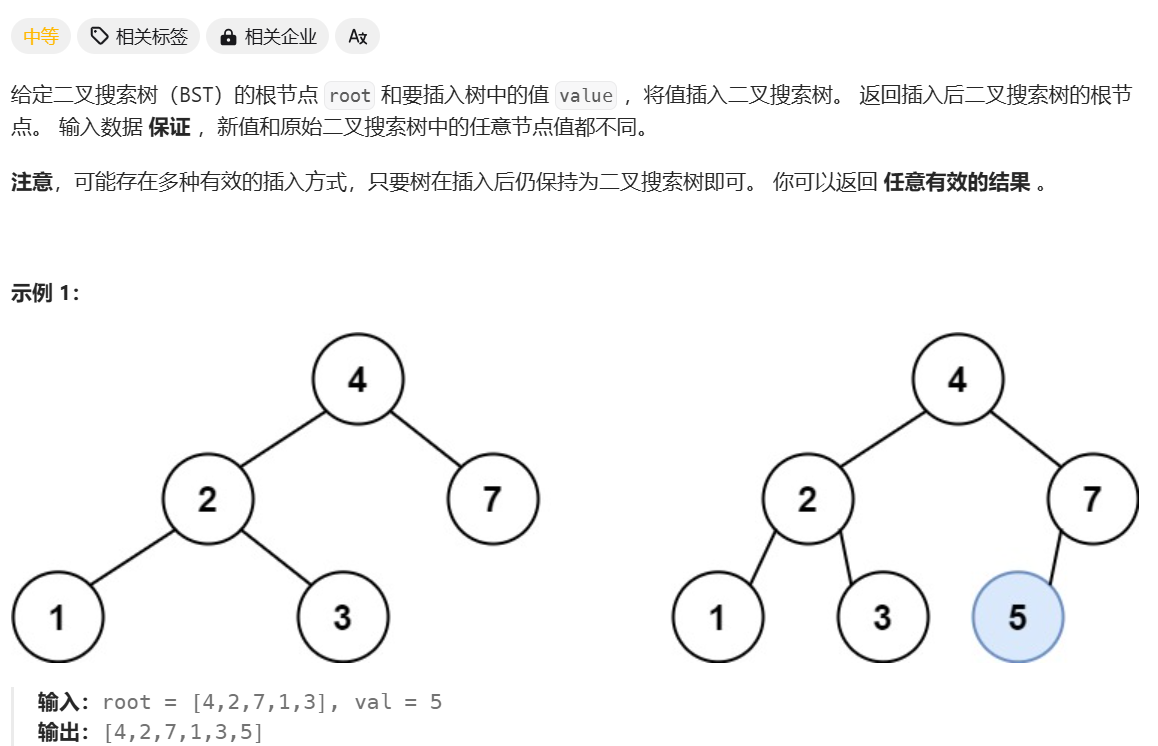
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if (root == null) { // 如果当前节点为空,也就意味着val找到了合适的位置,此时创建节点直接返回。
return new TreeNode(val);
}
if (root.val < val) {
root.right = insertIntoBST(root.right, val);
} else if (root.val > val) {
root.left = insertIntoBST(root.left, val);
}
return root;
}
}
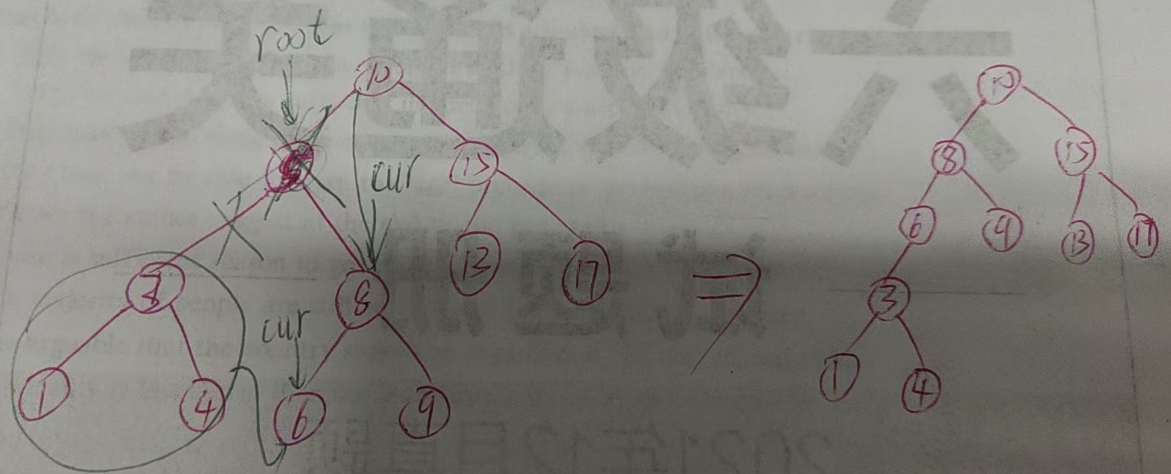
删除二叉搜索树中的节点
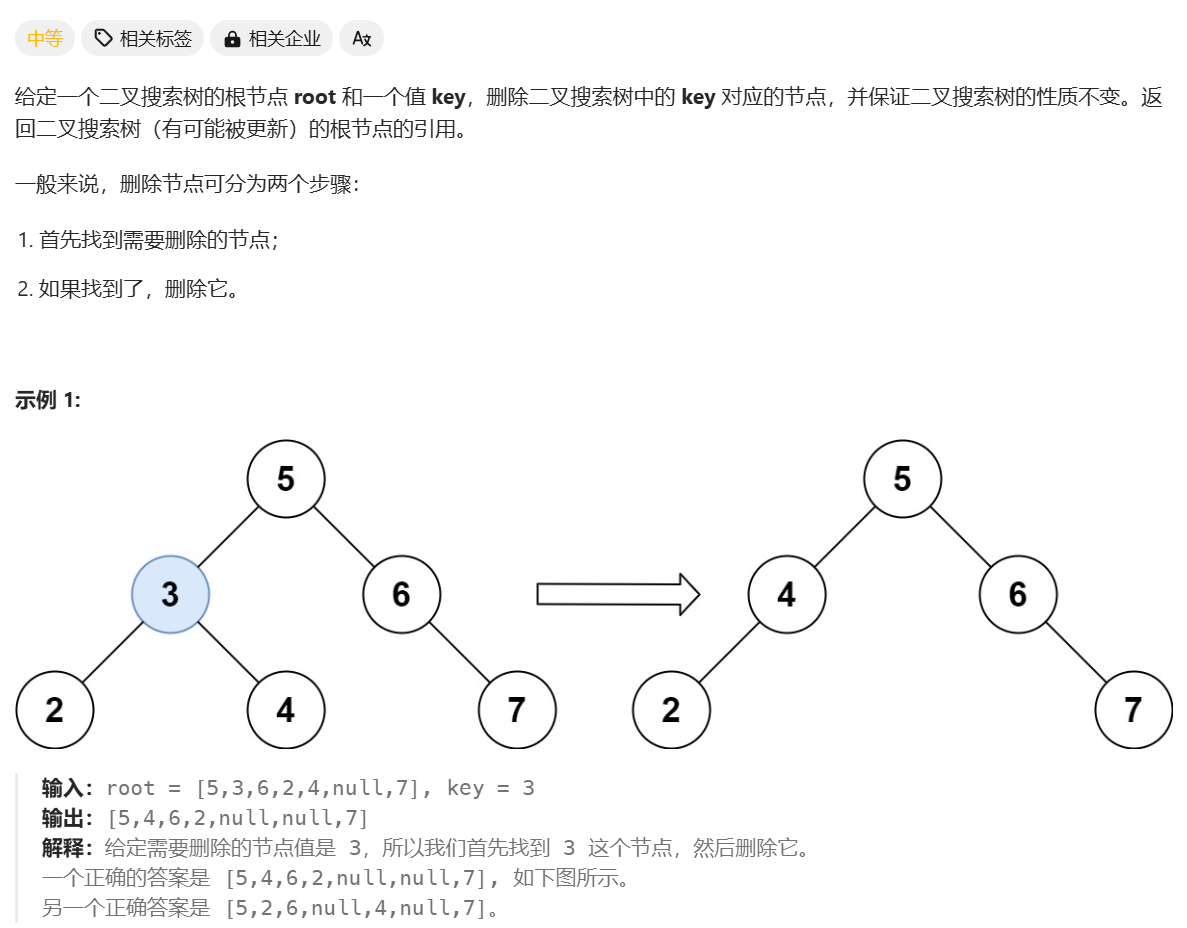
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return root;
if (root.val == key) {
if (root.left == null) {
return root.right;
} else if (root.right == null) {
return root.left;
} else {
TreeNode cur = root.right;
while (cur.left != null) {
cur = cur.left;
}
cur.left = root.left;
root = root.right;
return root;
}
}
if (root.val > key) {
root.left = deleteNode(root.left, key);
}
if (root.val < key) {
root.right = deleteNode(root.right, key);
}
return root;
}
}
修剪二叉搜索树
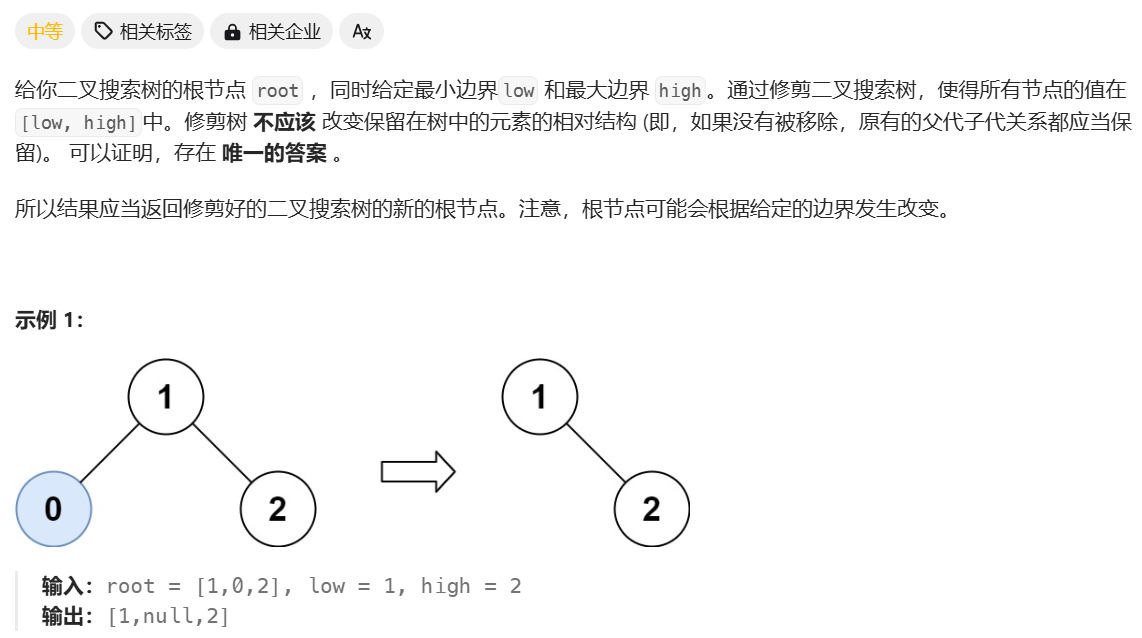
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
if (root == null) return null;
if (root.val < low) {
return trimBST(root.right, low, high);
}
if (root.val > high) {
return trimBST(root.left, low, high);
}
// root在[low,high]范围内
root.left = trimBST(root.left, low, high);
root.right = trimBST(root.right, low, high);
return root;
}
}
将有序数组转换为二叉搜索树
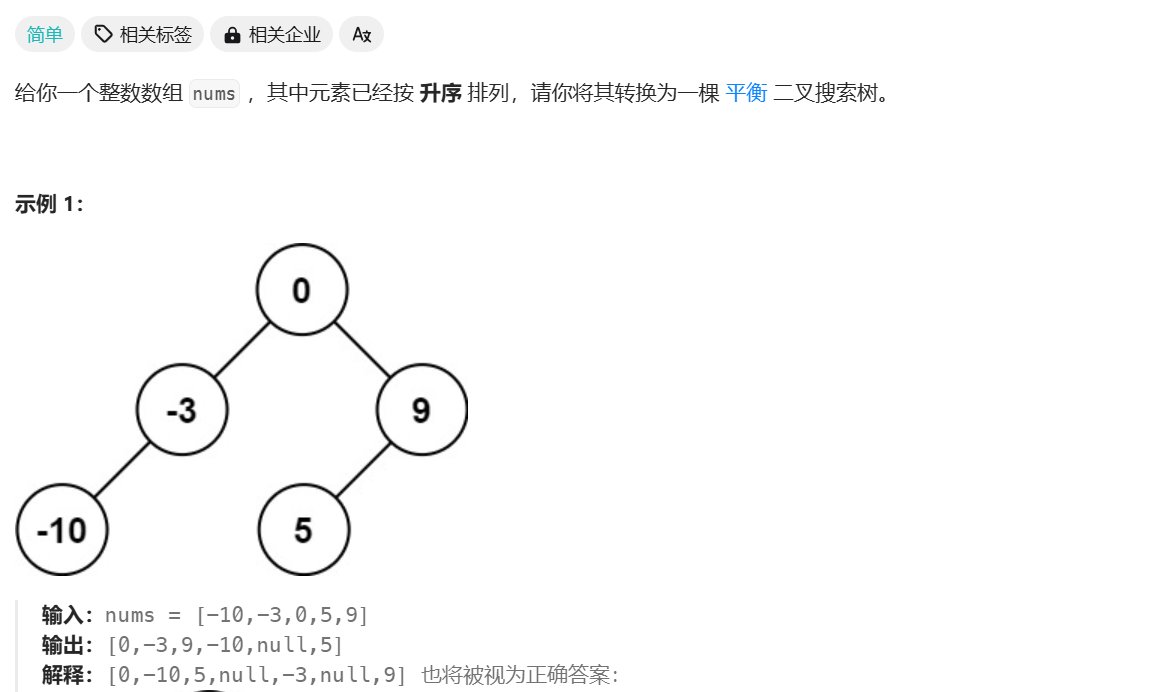
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return sortedArrayToBST(nums, 0, nums.length);
}
public TreeNode sortedArrayToBST(int[] nums, int left, int right) {
if (left >= right) {
return null;
}
if (right - left == 1) {
return new TreeNode(nums[left]);
}
int mid = left + (right - left) / 2;
TreeNode root = new TreeNode(nums[mid]);
root.left = sortedArrayToBST(nums, left, mid);
root.right = sortedArrayToBST(nums, mid + 1, right);
return root;
}
}
其实思路也是一样的,不断中间分割,然后递归处理左区间,右区间,也可以说是分治。
总结
节点带有构造函数

递归和迭代

最后,学习内容来源:
1)代码随想录
2)力扣


 浙公网安备 33010602011771号
浙公网安备 33010602011771号