8-2

37. 解数独

编写一个程序，通过已填充的空格来解决数独问题。

一个数独的解法需遵循如下规则：

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
空白格用 '.' 表示。

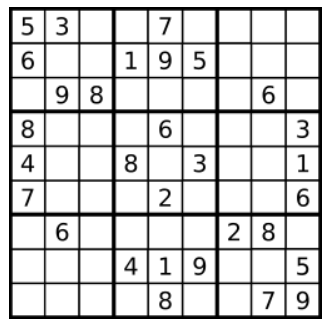
一个数独。

答案被标成红色。

Note:

给定的数独序列只包含数字 1-9 和字符 '.' 。
你可以假设给定的数独只有唯一解。
给定数独永远是 9x9 形式的。

An understandable python solution:

参考：https://leetcode.com/problems/sudoku-solver/discuss/140837/Python-very-simple-backtracking-solution-using-dictionaries-and-queue-_{100-ms-beats-}90

import collections
class Solution:
    def solveSudoku(self, board):
        rows, cols, triples, visit = collections.defaultdict(set), collections.defaultdict(set), collections.defaultdict(set), collections.deque([])
        for r in range(9):
            for c in range(9):
                if board[r][c] != ".":
                    rows[r].add(board[r][c])
                    cols[c].add(board[r][c])
                    triples[(r // 3, c // 3)].add(board[r][c])
                else:
                    visit.append((r, c))
        def dfs():
            if not visit:
                return True
            r, c = visit[0]
            t = (r // 3, c // 3)
            for dig in {"1", "2", "3", "4", "5", "6", "7", "8", "9"}:
                if dig not in rows[r] and dig not in cols[c] and dig not in triples[t]:
                    board[r][c] = dig
                    rows[r].add(dig)
                    cols[c].add(dig)
                    triples[t].add(dig)
                    visit.popleft()
                    if dfs():
                        return True
                    else:
                        board[r][c] = "."
                        rows[r].discard(dig)
                        cols[c].discard(dig)
                        triples[t].discard(dig)
                        visit.appendleft((r, c))
            return False
        dfs()

分析：

解这个数独问题的最基本的思路是什么呢？正如题目中给出的那个数独所示，假如说现在不让我们写程序，而是用“手撕”的方法把它做出来，那么我想我们大多数人的想法或许是这样的：

首先从第一行开始，我们发现第三个地方有空格，我们想在这个地方填上一个数字，以解决这个数独问题，但是这个空格应该填哪个数字呢？我们无从得知。一种笨方法是“试”：从最小的数字（1）开始，我们发现到目前为止在这个地方填1是可以的，因为这个空格所在的行、列以及3x3方阵（以下简称“阵”）中均没有数字1，因此目前来说在这里填1是合适的；

接下来我们来到第一行的第二个空格处，同样按照刚才“试”的方法，我们发现这里边可以填2（最好动手画一画，会有更深的理解），然后数字7后面的一个空格可以填4，倒数第三个空格可以填8，倒数第二个空格可以填9。好了，到这里先停一停，此时空格的填充情况如下图所示：

此时，当我们想要去填充第一行最后一个空格时，我们会发现不管我们填1-9之间的哪个数字，都无法满足数独的要求。这就说明我们前面填充的数字肯定是不合适的，这个时候问题来了：是它们都不合适，还是只有其中的某一个或某几个不合适？我们应该如何找到这个不合适的数字？又该做怎样的修改？这个时候，一种比较笨但比较稳妥的方法是：我们总是认为是上一个填充的空格中的数字不合适。例如，我们上一个填充的数字是9，现在我们认为这种填充是不合适的，因为我们是从最小的数字1开始不断地往数字大的方向去试的，而此时9已经是最大的数字了，因此9不合适只能说明是上一个填充的数字不合适，而上一个填充的数字是8，因此要把这里的8换成9（只能往大的方向去换，因为比8更小的数字我们都已经试过了）。

当倒数第三个空格换成9之后，倒数第二个空格仍旧需要从1开始试（就好像我们又重新到达了这个空格），我们发现这个空格只有填8才是满足要求的。

当倒数第二个空格填充完后，我们发现最后一个空格又没办法填了，这说明我们刚才的那一轮“回溯”（即修改我们以前填过的一些值）仍然没有彻底解决问题，此时我们还需要再“回溯”：倒数第二个空格有问题，但是倒数第二个空格已经没有别的值可以填了，那说明倒数第三个空格有问题；而倒数第三个空格已经是9了，那说明倒数第四个空格有问题，此时把倒数第四个空格换成5，然后我们再从1开始试探倒数第三个空格......

假如我们把往前不断试探的过程称为“正向试探”，把往后回溯纠错的过程称为“反向回溯”，那么整个求解这个数独的过程就可以看做是不断地“正向试探”和“反向回溯”的过程，而且在正向试探的过程中，我们总是从最小的数字1开始不断地往数字大的方向去试；在反向回溯的过程中，我们总是认为是上一个填充的空格中的数字不合适。因为题目假定给定的数独是有唯一解的，因此不断地重复上述两个过程之后，最终我们总能找到给定数独的一个解。

本文引用的代码正是基于以上描述而实现的。代码的实现思路如下：

（1）当我们要填充一个空格时，我们可以通过观察来判断我们要填的数字在当前的行、列、阵中是否有与之相同的元素，但是计算机是没有办法向我们一样去观察的。因此，首先我么要对给定的数独进行解析，解析的目标包括以下四个方面：

• 找出给定的数独总共有几行以及每行中都有哪些元素，以便后面在填充空格时判断与行内的元素是否有重复；
• 找出给定的数独总共有几列以及每列中都有哪些元素，以便后面在填充空格时判断与列内的元素是否有重复；
• 找出给定的数独总共有几个阵以及每个阵中都有哪些元素，以便后面在填充空格时判断与阵中的元素是否有重复；
• 找出给定的数独总共有多少个没有填充的空格，并记下它们的位置，以便后面对它们进行填充。

代码中这一解析过程是通过solveSudoku函数实现的，其中涉及到的一些函数的用法如下：

add方法

deque方法

collections.defaultdict()

collections.defaultdict()

（2）“正向试探”和“反向回溯”的过程是通过dfs函数实现的。

代码其实是在不断地递归的，但是这里的递归是有限度的，因为正向试探最多只会试探 \(9 \times 9 = 81\) 次（即给定的数独全是空格的情况），因此递归最多执行90次。

值得注意的是不管是“正向试探”还是“反向回溯”，rows、cols、triples以及visit中存储的值都是在不断变化的：

• 如果正向试探成功，则当前空格所在行、列、阵都要添加一项新的元素，以供其他位置的空格进行比较；
• 如果正向试探失败，则要把刚才那个空格中填的数删掉（即重新置成空格），然后把刚才添加到行、列、阵中的那个数去掉，把这个空格的位置重新加入到visit中，然后试探下一个数。

这里的一个巧妙之处是使用了deque，这样所有的操作都可以基于visit中的首个元素，而不用去考虑其他位置的元素。