leetcode刷题日记
unordered_set散列哈希表:C++ STL unordered_set容器完全攻略 (biancheng.net)
unordered_map:详细介绍C++STL:unordered_map - 朤尧 - 博客园 (cnblogs.com)
DAY1 数组
217. 存在重复元素
难度简单629
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
示例 1:
输入:nums = [1,2,3,1] 输出:true
示例 2:
输入:nums = [1,2,3,4] 输出:false
示例 3:
输入:nums = [1,1,1,3,3,4,3,2,4,2] 输出:true
法一:排序完判断前后是否相等即可
class Solution { public: bool containsDuplicate(vector<int>& nums) { sort(nums.begin(), nums.end()); for(int i=0;i<nums.size()-1;i++) { if(nums[i]==nums[i+1]) { return true; } } return false; } };
时间复杂度是排序的O(nlogn)
法二:如果存入的不是哈希表最后一个元素,则就有重复元素。
unordered_set
class Solution { public: bool containsDuplicate(vector<int>& nums) { unordered_set<int> a; for(int n:nums) { if(a.find(n)!=a.end()) return true; a.insert(n); } return false; } };
时间复杂度是O(n)
53. 最大子数组和
难度简单4385
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1] 输出:1
示例 3:
输入:nums = [5,4,-1,7,8] 输出:23
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
class Solution { public: int maxSubArray(vector<int>& nums) { int pre = 0, maxAns = nums[0]; for (auto x: nums) { pre = max(pre + x, x); maxAns = max(maxAns, pre); } return maxAns; } };
DAY2 数组
1. 两数之和
难度简单
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9 输出:[0,1] 解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6 输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6 输出:[0,1]
我的思路:直接遍历==target,暴力解法。
复杂度分析
时间复杂度:O(N^2),其中 NN 是数组中的元素数量。最坏情况下数组中任意两个数都要被匹配一次。
空间复杂度:O(1)
class Solution { public: vector<int> twoSum(vector<int>& nums, int target) { for(int i=0;i<nums.size()-1;i++) { for(int j=i+1;j<nums.size();j++) { if(nums[i]+nums[j]==target) return {i,j}; } } return {}; } };
法二:使用哈希表map,当哈希表中target-key不是最后一个哈希表元素,则返回value。
unordered_map
class Solution { public: vector<int> twoSum(vector<int>& nums, int target) { unordered_map<int, int> hashtable; for (int i = 0; i < nums.size(); i++) { //auto it即可 unordered_map<int, int>::iterator it = hashtable.find(target - nums[i]); if (it != hashtable.end()) return { it->second,i }; hashtable[nums[i]] = i; } return {}; } };
88. 合并两个有序数组
难度简单1291
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 输出:[1,2,2,3,5,6] 解释:需要合并 [1,2,3] 和 [2,5,6] 。 合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0 输出:[1] 解释:需要合并 [1] 和 [] 。 合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1 输出:[1] 解释:需要合并的数组是 [] 和 [1] 。 合并结果是 [1] 。 注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
法一:就移到一个数组里排序就好了
class Solution { public: void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) { for (int i = 0; i < n; i++) { nums1[m+i] = nums2[i]; } sort(nums1.begin(), nums1.end()); } };
时间复杂度就是排序O(nlogn)
法二:双指针遍历两个数组比大小
class Solution { public: void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) { int p1=0,p2=0; int sort[m+n]; int cur; int i=0; while(p1<m||p2<n) { if(p1==m) cur=nums2[p2++]; else if(p2==n) cur=nums1[p1++]; else if(nums1[p1]<nums2[p2]) cur=nums1[p1++]; else cur=nums2[p2++]; sort[i++]=cur; //sort[p1+p2-1]=cur; } for(i=0;i<m+n;i++) { nums1[i]=sort[i]; } } };
时间复杂度就是O(m+n)
DAY3 数组
350. 两个数组的交集 II
难度简单659
给你两个整数数组 nums1 和 nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现次数不一致,则考虑取较小值)。可以不考虑输出结果的顺序。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2] 输出:[2,2]
示例 2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4] 输出:[4,9]
法一:排序+双指针遍历。
class Solution { public: vector<int> intersect(vector<int>& nums1, vector<int>& nums2) { sort(nums1.begin(), nums1.end()); sort(nums2.begin(), nums2.end()); int p1 = 0, p2 = 0; int m = nums1.size(), n = nums2.size(); vector<int> a; while (p1 < m && p2 < n) { if (nums1[p1] < nums2[p2]) p1++; else if (nums1[p1] > nums2[p2]) p2++; else { a.push_back(nums1[p1]); p1++; p2++; } } return a; } };
unordered_map
方法二:哈希表
由于同一个数字在两个数组中都可能出现多次,因此需要用哈希表存储每个数字出现的次数。对于一个数字,其在交集中出现的次数等于该数字在两个数组中出现次数的最小值。
首先遍历第一个数组,并在哈希表中记录第一个数组中的每个数字以及对应出现的次数,然后遍历第二个数组,对于第二个数组中的每个数字,如果在哈希表中存在这个数字,则将该数字添加到答案,并减少哈希表中该数字出现的次数。
为了降低空间复杂度,首先遍历较短的数组并在哈希表中记录每个数字以及对应出现的次数,然后遍历较长的数组得到交集。
class Solution { public: vector<int> intersect(vector<int>& nums1, vector<int>& nums2) { int m = nums1.size(), n = nums2.size(); vector<int> a; unordered_map<int, int> hashtable; for (int i = 0; i < m; i++) { auto it = hashtable.find(nums1[i]); if (it != hashtable.end()) { it->second++; } else hashtable.insert(pair<int, int>(nums1[i], 1)); } for (int i = 0; i < n; i++) { auto it = hashtable.find(nums2[i]); if (it != hashtable.end()) { a.push_back(it->first); it->second--; if (it->second == 0) hashtable.erase(nums2[i]); } } return a; } };
时间复杂度:O(m+n)
空间复杂度:O(n)
121. 买卖股票的最佳时机
难度简单2133
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4] 输出:5 解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
方法一:暴力解法,后面的数减前面的数,得到最大值为止
int ans = 0; for (int i = 0; i < prices.size()-1; i++) { for (int j = i + 1; j < prices.size(); j++) { ans =max(ans, prices[j] - prices[i]); } } return ans;
时间复杂度:O(n^2)循环运行 n (n-1)/2 次。
空间复杂度:O(1)。只使用了常数个变量。
这个解法提交过不了,超出时间限制了。
动态规划
方法二:假如计划在第 i 天卖出股票,那么最大利润的差值一定是在[0, i-1] 之间选最低点买入;所以遍历数组,依次求每个卖出时机的的最大差值,再从中取最大值。
class Solution { public: int maxProfit(vector<int>& prices) { int inf = 1e9; int minprice = inf, maxprofit = 0; for (int price: prices) { maxprofit = max(maxprofit, price - minprice); minprice = min(price, minprice); } return maxprofit; } };
- 时间复杂度:O(n),只需要遍历一次。
- 空间复杂度:O(1),只使用了常数个变量。
二分查找
704. 二分查找
难度简单654
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9 输出: 4 解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2 输出: -1 解释: 2 不存在 nums 中因此返回 -1
int search(vector<int>& nums, int target) { sort(nums.begin(), nums.end()); int left = 0, right = nums.size() - 1; while (left <= right) { int mid = (right - left) / 2 + left; if (target < nums[mid]) right = mid - 1; else if (target > nums[mid]) left = mid + 1; else return mid; } return -1; }
时间复杂度是O(logn)
278. 第一个错误的版本
难度简单586
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, ..., n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
示例 1:
输入:n = 5, bad = 4 输出:4 解释: 调用 isBadVersion(3) -> false 调用 isBadVersion(5) -> true 调用 isBadVersion(4) -> true 所以,4 是第一个错误的版本。
示例 2:
输入:n = 1, bad = 1 输出:1
关键在于循环条件left是<或者<=right,以及left=mid+1或者feft=mid左右界的范围。
class Solution { public: int firstBadVersion(int n) { int left = 1, right = n; while (left < right) { // 循环直至区间左右端点相同 int mid = left + (right - left) / 2; // 防止计算时溢出 if (isBadVersion(mid)) { right = mid; // 答案在区间 [left, mid] 中 } else { left = mid + 1; // 答案在区间 [mid+1, right] 中 } } // 此时有 left == right,区间缩为一个点,即为答案 return left; } };
35. 搜索插入位置
难度简单1357
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5 输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2 输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7 输出: 4
示例 4:
输入: nums = [1,3,5,6], target = 0 输出: 0
示例 5:
输入: nums = [1], target = 0 输出: 0
class Solution { public: int searchInsert(vector<int>& nums, int target) { int n = nums.size(); int left = 0, right = n - 1, ans = n; while (left <= right) { int mid = ((right - left) >> 1) + left; if (target <= nums[mid]) { ans = mid; right = mid - 1; } else { left = mid + 1; } } return ans; } };
DAY4 数组
566. 重塑矩阵
难度简单282
在 MATLAB 中,有一个非常有用的函数 reshape ,它可以将一个 m x n 矩阵重塑为另一个大小不同(r x c)的新矩阵,但保留其原始数据。
给你一个由二维数组 mat 表示的 m x n 矩阵,以及两个正整数 r 和 c ,分别表示想要的重构的矩阵的行数和列数。
重构后的矩阵需要将原始矩阵的所有元素以相同的 行遍历顺序 填充。
如果具有给定参数的 reshape 操作是可行且合理的,则输出新的重塑矩阵;否则,输出原始矩阵。
示例 1:
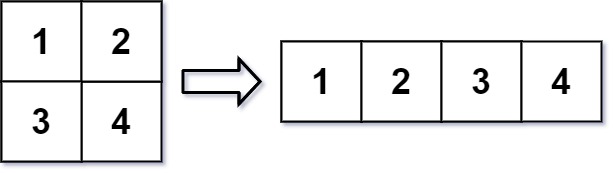
输入:mat = [[1,2],[3,4]], r = 1, c = 4 输出:[[1,2,3,4]]
示例 2:

输入:mat = [[1,2],[3,4]], r = 2, c = 4 输出:[[1,2],[3,4]]
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 100-1000 <= mat[i][j] <= 10001 <= r, c <= 300
思路:二维数组的映射为:
(i,j)→i×n+j
同样地,我们可以将整数 xx 映射回其在矩阵中的下标,即
- i=x / n
j=x % n
其中 / 表示整数除法,% 表示取模运算。
那么题目需要我们做的事情相当于:
将二维数组 nums 映射成一个一维数组;
将这个一维数组映射回 r 行 c 列的二维数组。
我们当然可以直接使用一个一维数组进行过渡,但我们也可以直接从二维数组 nums 得到 r 行 c 列的重塑矩阵:
设 nums 本身为 m 行 n 列,如果 mn=rc,那么二者包含的元素个数不相同,因此无法进行重塑;
否则,对于x∈[0,mn),第 x 个元素在 中对应的下标为 (x / n,x % n),而在新的重塑矩阵中对应的下标为 (x / c,x % c)。我们直接进行赋值即可。
vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) { int m = mat.size(); int n = mat[0].size(); if (m * n != r * c) return mat; else { //vector<vector<int>> a;rc矩阵 vector<vector<int>> a(r, vector<int>(c)); for (int x = 0; x < m * n; x++) { a[x / c][x % c] = mat[x / n][x % n]; } return a; }
118. 杨辉三角
难度简单694
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。

示例 1:
输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1 输出: [[1]]
vector<vector<int>> generate(int numRows) { vector<vector<int>> ret(numRows); for (int i = 0; i < numRows; i++) { ret[i].resize(i + 1); //令ret[i]的大小为i+1 ret[i][0] = ret[i][i] = 1; //头尾都为1 for (int j = 1; j < i; j++) { ret[i][j] = ret[i - 1][j - 1] + ret[i - 1][j]; } } return ret; }
复杂度分析
- 时间复杂度:O(numRows^2)。
- 空间复杂度:O(1)。不考虑返回值的空间占用。
DAY5 数组
36. 有效的数独
难度中等780
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
注意:
- 一个有效的数独(部分已被填充)不一定是可解的。
- 只需要根据以上规则,验证已经填入的数字是否有效即可。
- 空白格用
'.'表示。
示例 1:

输入:board = [["5","3",".",".","7",".",".",".","."] ,["6",".",".","1","9","5",".",".","."] ,[".","9","8",".",".",".",".","6","."] ,["8",".",".",".","6",".",".",".","3"] ,["4",".",".","8",".","3",".",".","1"] ,["7",".",".",".","2",".",".",".","6"] ,[".","6",".",".",".",".","2","8","."] ,[".",".",".","4","1","9",".",".","5"] ,[".",".",".",".","8",".",".","7","9"]] 输出:true
示例 2:
输入:board = [["8","3",".",".","7",".",".",".","."] ,["6",".",".","1","9","5",".",".","."] ,[".","9","8",".",".",".",".","6","."] ,["8",".",".",".","6",".",".",".","3"] ,["4",".",".","8",".","3",".",".","1"] ,["7",".",".",".","2",".",".",".","6"] ,[".","6",".",".",".",".","2","8","."] ,[".",".",".","4","1","9",".",".","5"] ,[".",".",".",".","8",".",".","7","9"]] 输出:false 解释:除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
bool isValidSudoku(vector<vector<char>>& board) { //分别判断行列和九宫格的数组 int rows[9][9]; int columns[9][9]; int subboxes[3][3][9]; //将数组全部初始化0 memset(rows, 0, sizeof(rows)); memset(columns, 0, sizeof(columns)); memset(subboxes, 0, sizeof(subboxes)); for (int i = 0; i < 9; i++) { for (int j = 0; j < 9; j++) { char c = board[i][j]; if (c != '.') { int index = c - '0' - 1; //c-'0'获得这个数字,-1对应数组中的位置 //这个一次把三个数组都添加的方法挺好的 rows[i][index]++; columns[j][index]++; subboxes[i / 3][j / 3][index]++; if (rows[i][index] > 1 || columns[j][index] > 1 || subboxes[i / 3][j / 3][index] > 1) { return false; } } } } return true; }
73. 矩阵置零
难度中等661
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1:

输入:matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:

输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] 输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
class Solution { public: void setZeroes(vector<vector<int>>& matrix) { int m = matrix.size(); int n = matrix[0].size(); //设置一个判断数组 vector<int> row(m), col(n); for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { if (matrix[i][j] == 0) { row[i] = 1; col[j] = 1; } } } for (int i = 0; i < m; i++) for (int j = 0; j < n; j++) if (row[i] || col[j]) matrix[i][j] = 0; } };
189. 轮转数组
难度中等1346
给你一个数组,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,3,4,5] 向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2 输出:[3,99,-1,-100] 解释: 向右轮转 1 步: [99,-1,-100,3] 向右轮转 2 步: [3,99,-1,-100]
法一:找到规律ans[(i+k)%m]=nums[i]
void rotate(vector<int>& nums, int k) { int m = nums.size(); //这里有一个关键点 必须指定ans的大小,后续才能使用ans[i]的形式 vector<int> ans(m); for(int i=0;i<m;i++) { ans[(i+k)%m]=nums[i]; } //这是一个拷贝函数,还可以将n个x赋值:nums.assign(n,x); nums.assign(ans.begin(), ans.end()); }
- 时间复杂度: O(n),其中 n 为数组的长度。
- 空间复杂度: O(n)。
法二:我们以 n=7n=7,k=3k=3 为例进行如下展示:
操作 结果
原始数组 1 2 3 4 5 6 7
翻转所有元素 7 6 5 4 3 2 1
翻转[0,kmodn−1] 区间的元素 5 6 7 4 3 2 1
翻转[kmodn,n−1] 区间的元素 5 6 7 1 2 3 4
void reverse(vector<int>& nums, int start, int end) { while (start < end) { swap(nums[start], nums[end]); start += 1; end -= 1; } } void rotate(vector<int>& nums, int k) { k %= nums.size(); reverse(nums, 0, nums.size() - 1); reverse(nums, 0, k - 1); reverse(nums, k, nums.size() - 1); }
时间复杂度:O(n),其中 nn 为数组的长度。每个元素被翻转两次,一共 nn 个元素,因此总时间复杂度为 O(2n)=O(n)O(2n)=O(n)。
空间复杂度:O(1)。
DAY6 字符串
链表具有递归的性质,所以链表的题目常常可以用递归解题。
387. 字符串中的第一个唯一字符
难度简单510
给定一个字符串 s ,找到 它的第一个不重复的字符,并返回它的索引 。如果不存在,则返回 -1 。
unordered_map
示例 1:
输入: s = "leetcode" 输出: 0
示例 2:
输入: s = "loveleetcode" 输出: 2
示例 3:
输入: s = "aabb" 输出: -1
int firstUniqChar(string s) { unordered_map<char, int> hashtable; int m = s.size(); for (int i = 0; i < m; i++) { hashtable[s[i]]++; } for (int i = 0; i < m; i++) { auto it = hashtable.find(s[i]); if(it->second==1) return i; } return -1; }
383. 赎金信
难度简单278
给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。
如果可以,返回 true ;否则返回 false 。
magazine 中的每个字符只能在 ransomNote 中使用一次。
示例 1:
输入:ransomNote = "a", magazine = "b" 输出:false
示例 2:
输入:ransomNote = "aa", magazine = "ab" 输出:false
示例 3:
输入:ransomNote = "aa", magazine = "aab" 输出:true
思路:就用哈希表
unordered_map<char, int> hashtable; for (char a : magazine) { hashtable[a]++; } for (char a : ransomNote) { auto it = hashtable.find(a); if (it == hashtable.end()) return false; else { hashtable[a]--; if (it->second < 0) return false; } } return true;
用时较长,所以考虑直接用数组存每个字母
bool canConstruct(string ransomNote, string magazine) { if (ransomNote.size() > magazine.size()) { return false; } vector<int> cnt(26); for (auto & c : magazine) { cnt[c - 'a']++; } for (auto & c : ransomNote) { cnt[c - 'a']--; if (cnt[c - 'a'] < 0) { return false; } } return true; }
DAY7 链表
141. 环形链表
难度简单1363
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例 1:

输入:head = [3,2,0,-4], pos = 1 输出:true 解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:

输入:head = [1,2], pos = 0 输出:true 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1 输出:false 解释:链表中没有环。
class Solution { public: bool hasCycle(ListNode *head) { ListNode* slow, * fast; slow = fast = head; if (head == nullptr || head->next == nullptr) return false; while (fast != nullptr && fast->next != nullptr) { fast = fast->next->next; slow = slow->next; if (fast == slow) { return true; } } return false; } };
时间复杂度:O(N),其中 NN 是链表中的节点数。
当链表中不存在环时,快指针将先于慢指针到达链表尾部,链表中每个节点至多被访问两次。
当链表中存在环时,每一轮移动后,快慢指针的距离将减小一。而初始距离为环的长度,因此至多移动 NN 轮。
空间复杂度:O(1)。我们只使用了两个指针的额外空间。
21. 合并两个有序链表
难度简单2212
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:

输入:l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]
示例 2:
输入:l1 = [], l2 = [] 输出:[]
示例 3:
输入:l1 = [], l2 = [0] 输出:[0]
法一:最简单的判断下去加入新链表的方法
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) { ListNode ans = ListNode(); ListNode* p = &ans; while (list1 != nullptr && list2 != nullptr) { if (list1->val < list2->val) { p->next = list1; list1 = list1->next; } else { p->next = list2; list2 = list2->next; } p = p->next; } //这行代码太强了,处理剩下的元素 p->next = list1 == nullptr ? list2 : list1; return ans.next; }
时间复杂度和空间复杂度都是O(m+n)
法二:递归。
如果 l1 或者 l2 一开始就是空链表 ,那么没有任何操作需要合并,所以我们只需要返回非空链表。否则,我们要判断 l1 和 l2 哪一个链表的头节点的值更小,然后递归地决定下一个添加到结果里的节点。如果两个链表有一个为空,递归结束。
class Solution { public: ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) { if (l1 == nullptr) { return l2; } else if (l2 == nullptr) { return l1; } else if (l1->val < l2->val) { l1->next = mergeTwoLists(l1->next, l2); return l1; } else { l2->next = mergeTwoLists(l1, l2->next); return l2; } } };
时间复杂度:O(m+n)
空间复杂度:O(1)
203. 移除链表元素
难度简单814
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
示例 1:
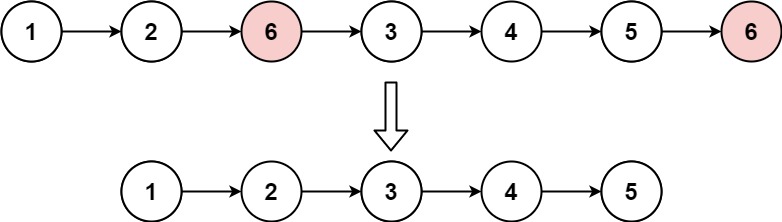
输入:head = [1,2,6,3,4,5,6], val = 6 输出:[1,2,3,4,5]
示例 2:
输入:head = [], val = 1 输出:[]
示例 3:
输入:head = [7,7,7,7], val = 7 输出:[]
法一:递归
ListNode* removeElements(ListNode* head, int val) { if(head==nullptr) return head; head->next = removeElements(head->next, val); return head->val == val ? head->next : head; }
DAY8 链表
206. 反转链表
难度简单2315
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:

输入:head = [1,2,3,4,5] 输出:[5,4,3,2,1]
示例 2:

输入:head = [1,2] 输出:[2,1]
示例 3:
输入:head = [] 输出:[]
class Solution { public: ListNode* reverseList(ListNode* head) { ListNode* prev = nullptr; ListNode* curr = head; while (curr) { ListNode* next = curr->next; curr->next = prev; prev = curr; curr = next; } return prev; } };
先将cur->next改成->pre,然后pre右移,cur右移。
83. 删除排序链表中的重复元素
难度简单736
给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表 。
示例 1:
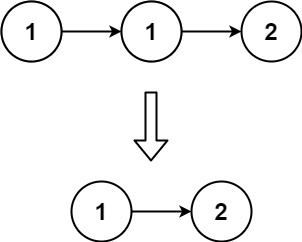
输入:head = [1,1,2] 输出:[1,2]
示例 2:
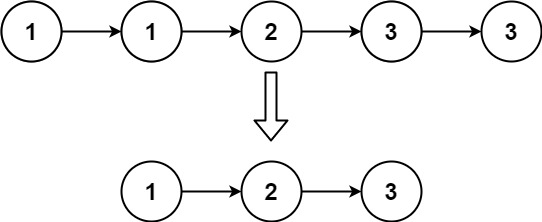
输入:head = [1,1,2,3,3] 输出:[1,2,3]
思路:就遍历删节点。
class Solution { public: ListNode* deleteDuplicates(ListNode* head) { ListNode* p=head; if(!head) return head; while(p->next) { if(p->val==p->next->val) p->next=p->next->next; else p=p->next; } return head; } };
DAY9 栈和队列
20. 有效的括号
难度简单3026
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
示例 1:
输入:s = "()" 输出:true
示例 2:
输入:s = "()[]{}" 输出:true
示例 3:
输入:s = "(]" 输出:false
示例 4:
输入:s = "([)]" 输出:false
示例 5:
输入:s = "{[]}" 输出:true
法一:用栈匹配,左括号依次入栈,当遇到右括号时,则需要与栈顶元素做匹配。
class Solution { public: bool isValid(string s) { int n = s.size(); if (n % 2 == 1) { return false; } unordered_map<char, char> hashtable = { {')', '('}, {']', '['}, {'}', '{'} }; stack<char> stack; for (char a: s) { //如果hashtable中存在键值a,返回1,否则返回0 //if a 是右括号的意思 if (hashtable.count(a)) { //如果有右括号但是栈是空的或者栈顶不等于左括号 if (stack.empty() || stack.top() != hashtable[a]) return false; stack.pop(); } //左括号入栈 else { stack.push(a); } } return stack.empty(); } };
232. 用栈实现队列
难度简单
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x)将元素 x 推到队列的末尾int pop()从队列的开头移除并返回元素int peek()返回队列开头的元素boolean empty()如果队列为空,返回true;否则,返回false
说明:
- 你 只能 使用标准的栈操作 —— 也就是只有
push to top,peek/pop from top,size, 和is empty操作是合法的。 - 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
示例 1:
输入: ["MyQueue", "push", "push", "peek", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 1, 1, false] 解释: MyQueue myQueue = new MyQueue(); myQueue.push(1); // queue is: [1] myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue) myQueue.peek(); // return 1 myQueue.pop(); // return 1, queue is [2] myQueue.empty(); // return false
提示:
1 <= x <= 9- 最多调用
100次push、pop、peek和empty - 假设所有操作都是有效的 (例如,一个空的队列不会调用
pop或者peek操作)
进阶:
- 你能否实现每个操作均摊时间复杂度为
O(1)的队列?换句话说,执行n个操作的总时间复杂度为O(n),即使其中一个操作可能花费较长时间。
思路:用两个栈即可,一个负责入栈一个负责出栈。
(6条消息) 两个栈实现一个队列_ailunlee的博客-CSDN博客_两个栈实现一个队列
class MyQueue { private: stack<int> inStack, outStack; void in2out() { while (!inStack.empty()) { outStack.push(inStack.top()); inStack.pop(); } } public: MyQueue() {} void push(int x) { inStack.push(x); } int pop() { if (outStack.empty()) { in2out(); } int x = outStack.top(); outStack.pop(); return x; } int peek() { if (outStack.empty()) { in2out(); } return outStack.top(); } bool empty() { return inStack.empty() && outStack.empty(); } };
DAY10 二叉树
144. 二叉树的前中后序遍历
深度优先搜索
难度简单741
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
前序:根节点,左子树,右子树。
中序:左子树,根节点,右子树。
后序:左子树,右子树,根节点。
示例 1:

输入:root = [1,null,2,3] 输出:[1,2,3]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
示例 4:

输入:root = [1,2] 输出:[1,2]
示例 5:

输入:root = [1,null,2] 输出:[1,2]
递归
class Solution { public: void preorder(TreeNode* root,vector<int> &res) { if (root == nullptr) return; res.push_back(root->val); preorder(root->left, res); preorder(root->right, res); } void inorder(TreeNode* root, vector<int>& res) { if (root == nullptr) return; inorder(root->left, res); res.push_back(root->val); inorder(root->right, res); } void postorder(TreeNode *root,vector<int> &res) { if(root==nullptr) return; postorder(root->left,res); postorder(root->right,res); res.push_back(root->val); } vector<int> preorderTraversal(TreeNode* root) { vector<int> res; preorder(root, res); return res; } };
迭代
我们也可以用迭代的方式实现方法一的递归函数,两种方式是等价的,区别在于递归的时候隐式地维护了一个栈,而我们在迭代的时候需要显式地将这个栈模拟出来,其余的实现与细节都相同,具体可以参考下面的代码。
vector<int> preorderTraversal(TreeNode* root) { vector<int> res; if (!root) return res; //遍历节点 左子树 右子树 stack<TreeNode*> stk; TreeNode* node = root; //当栈不为空或者节点有指向时 while (!stk.empty() || node) { //当节点不为空时,一直向左子树遍历下去 while (node) { //将节点添加入数组中 res.emplace_back(node->val); //将节点记录在栈中 stk.emplace(node); node = node->left; } //如果节点遍历到底了,节点就指回栈顶元素,看看有没有右子树,有右子树的话接着循环 //没有右子树的话,看栈里面还有没有元素,返回栈顶元素,接着循环 node = stk.top(); stk.pop(); node = node->right; } return res; } vector<int> inorderTraversal(TreeNode* root) { vector<int> res; if (!root) return res; //左子树 根节点 右子树 stack<TreeNode*> stk; TreeNode* node = root; while (!stk.empty() || node) { //遍历至最左节点 将这些左节点全部加入栈 while (node) { stk.emplace(node); node = node->left; } //节点返回栈顶元素,并将栈顶元素加入数组,节点指向右子树如果没有右子树,那就返回栈顶节点 //如果有右子树,那么接着从这个右节点去遍历它的左子树 node = stk.top(); stk.pop(); res.emplace_back(node->val); node = node->right; } return res; } vector<int> postorderTraversal(TreeNode *root) { vector<int> res; if (root == nullptr) return res; //左子树 右子树 根节点 stack<TreeNode *> stk; TreeNode *prev = nullptr; while (root || !stk.empty()) { //遍历至最左节点 将这些左节点全部加入栈 while (root) { stk.emplace(root); root = root->left; } //跟返回栈顶元素 root = stk.top(); stk.pop(); //如果栈顶元素没有右子树或者右子树等于前驱节点 if (root->right == nullptr || root->right == prev) { //将栈顶元素入数组 res.emplace_back(root->val); //前驱指向当前栈顶元素,当前节点设空,则循环回到当前栈顶元素 //栈顶元素就是刚刚入栈的左子树的根节点,去判断根节点有没有右子树 prev = root; root = nullptr; } //如果栈顶元素有右子树,那么接着往右子树遍历下去加入栈 //遍历到右子树底的时候,返回当前栈顶元素即右子树底 //右子树底后,就将右子树底进入数组,即可完成先进左子树 再进右子树 记录下现在的右子树节点 //回右子树的前一个节点 发现它是根节点 z else { stk.emplace(root); root = root->right; } } return res; }
283. 移动零
难度简单1457
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12] 输出: [1,3,12,0,0]
示例 2:
输入: nums = [0] 输出: [0]
思路:把非零的数字先加入数组,然后补零。
void moveZeroes(vector<int>& nums) { int index=0; for(auto x:nums) if(x) nums[index++]=x; for(int i=index;i<nums.size();i++) nums[i]=0; }
双指针:思路及解法
使用双指针,左指针指向当前已经处理好的序列的尾部,右指针指向待处理序列的头部。
右指针不断向右移动,每次右指针指向非零数,则将左右指针对应的数交换,同时左指针右移。
注意到以下性质:
左指针左边均为非零数;
右指针左边直到左指针处均为零。
因此每次交换,都是将左指针的零与右指针的非零数交换,且非零数的相对顺序并未改变。
void moveZeroes(vector<int>& nums) { int n = nums.size(), left = 0, right = 0; //左指针指向当前已经处理好的序列的尾部,右指针指向待处理序列的头部。 while(right<nums.size()) { //如果右指针指的数字是非零,那么左右指针的数字交换 if(nums[right]) { swap(nums[left],nums[right]); left++; } //如果右指针指的数字是零,右指针右移,左指针指向的数字就是零 right++; } }
DAY11 二叉树
102. 二叉树的层序遍历
难度中等1200
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:

输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1] 输出:[[1]]
示例 3:
输入:root = [] 输出:[]
法一:迭代
广度优先搜索
队列实现:
仔细看看层序遍历过程,其实就是从上到下,从左到右依次将每个数放入到队列中,然后按顺序依次打印就是想要的结果。
实现过程
1、首先将二叉树的根节点push到队列中,判断队列不为NULL,就输出队头的元素,
2、判断节点如果有孩子,就将孩子push到队列中,
3、遍历过的节点出队列,
4、循环以上操作,直到Tree == NULL。
void FloorPrint_QUEUE(pTreeNode &Tree) //层序遍历_队列实现 { queue < pTreeNode> q; if (Tree != NULL) { q.push(Tree); //根节点进队列 } while (q.empty() == false) //队列不为空判断 { cout << q.front()->data << " → "; if (q.front()->leftPtr != NULL) //如果有左孩子,leftChild入队列 { q.push(q.front()->leftPtr); } if (q.front()->rightPtr != NULL) //如果有右孩子,rightChild入队列 { q.push(q.front()->rightPtr); } q.pop(); //已经遍历过的节点出队列 } }
vector<vector<int>> levelOrder(TreeNode* root) { vector<vector<int>> res; if (!root) return res; queue<TreeNode*> queue; queue.push(root); while (!queue.empty()) { int curLevelSize = queue.size(); res.push_back(vector<int>()); //每一层先添加一个空数组 for (int i = 0; i < curLevelSize; i++) { TreeNode* node = queue.front(); //返回大数组最后一个数组,并加入node指向的数字 res.back().push_back(node->val); //如果有左孩子,leftChild入队列 if (node->left) queue.push(node->left); if (node->right) queue.push(node->right); queue.pop(); //已经遍历过的节点出队列 } } return res; }
104. 二叉树的最大深度
难度简单1132
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3 / \ 9 20 / \ 15 7
返回它的最大深度 3 。
广度优先搜索
int maxDepth(TreeNode* root) { if(root==nullptr) return 0; int ans = 0; queue<TreeNode*> q; q.push(root); while (q.empty() == false) { int cur = q.size(); for (int i = 0; i < cur; i++) { auto node = q.front(); if (node->left) q.push(node->left); if (node->right) q.push(node->right); q.pop(); } ans++; } return ans; }
深度优先搜索
int maxDepth(TreeNode* root) { if (root == nullptr) return 0; return max(maxDepth(root->left), maxDepth(root->right)) + 1; }
101. 对称二叉树
难度简单1777
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:

输入:root = [1,2,2,3,4,4,3] 输出:true
示例 2:

输入:root = [1,2,2,null,3,null,3] 输出:false
break 作用:用于终止当前循环
break 如果用于循环是用来终止循环,break只能终止距离它最近的循环
break如果用于switch,则是用于终止switch
continue 作用:用以跳过本次循环余下的语句,转去判断是否需要执行下次循环
只作用于距离它最近的循环:for 、while 、do ...while
广度优先搜索
思路:初始化时我们把根节点入队两次。每次提取两个结点并比较它们的值(队列中每两个连续的结点应该是相等的,而且它们的子树互为镜像),然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时,或者我们检测到树不对称(即从队列中取出两个不相等的连续结点)时,该算法结束。
例一:q 11 2222 223344 33443344 443344 3344 44 true
例二:q 11 2222 22n33n n33nn33n 3nn33n node1=n false
bool cheak(TreeNode* u, TreeNode* v) { queue<TreeNode*> q; q.push(u); q.push(v); while (q.empty() == false) { TreeNode* node1 = q.front(); q.pop(); TreeNode* node2 = q.front(); q.pop(); if (node1 == nullptr && node2 == nullptr) continue; if (node1 == nullptr || node2 == nullptr || node1->val != node2->val) return false; q.push(node1->left); q.push(node2->right); q.push(node1->right); q.push(node2->left); } return true; } bool isSymmetric(TreeNode* root) { return cheak(root, root); }
深度优先搜索
class Solution { public: bool check(TreeNode *p, TreeNode *q) { //如果左右子树都是空则返回对 if (!p && !q) return true; if (!p || !q) return false; //检查当前节点的左右节点是否对称相等 return p->val == q->val && check(p->left, q->right) && check(p->right, q->left); } bool isSymmetric(TreeNode* root) { return check(root, root); } };
DAY12 二叉树
226. 翻转二叉树
难度简单1189
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:

输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]
示例 2:

输入:root = [2,1,3] 输出:[2,3,1]
示例 3:
输入:root = [] 输出:[]
广度优先搜索
TreeNode* invertTree(TreeNode* root) { queue<TreeNode*> q; q.push(root); if (!root) return root; while (!q.empty()) { auto node = q.front(); if (node->left) q.push(node->left); if (node->right) q.push(node->right); q.pop(); if (node->left || node->right) { TreeNode* newNode = node->left; node->left = node->right; node->right = newNode; } } return root; }
112. 路径总和
难度简单802
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出:true 解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:

输入:root = [1,2,3], targetSum = 5 输出:false 解释:树中存在两条根节点到叶子节点的路径: (1 --> 2): 和为 3 (1 --> 3): 和为 4 不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0 输出:false 解释:由于树是空的,所以不存在根节点到叶子节点的路径。
广度优先搜索
思路就是多加一个队列qsum用于记录每个节点到根节点的数字之和,然后比较target即可。
bool hasPathSum(TreeNode *root, int sum) { if (root == nullptr) return false; queue<TreeNode*> q; q.push(root); queue<int> qsum; qsum.push(root->val); while (!q.empty()) { auto node = q.front(); auto temp = qsum.front(); if (node->left == nullptr && node->right == nullptr) if (temp == sum) return true; if (node->left) { q.push(node->left); qsum.push(node->left->val + temp); } if (node->right) { q.push(node->right); qsum.push(node->right->val + temp); } q.pop(); qsum.pop(); } return false; }
DAY13 二叉搜索树
700. 二叉搜索树中的搜索
难度简单245
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
示例 1:
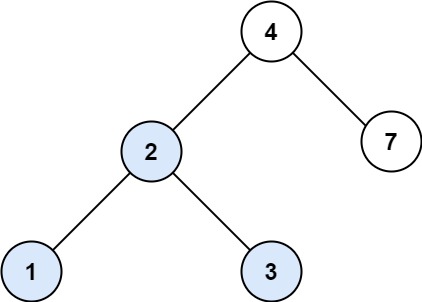
输入:root = [4,2,7,1,3], val = 2 输出:[2,1,3]
Example 2:
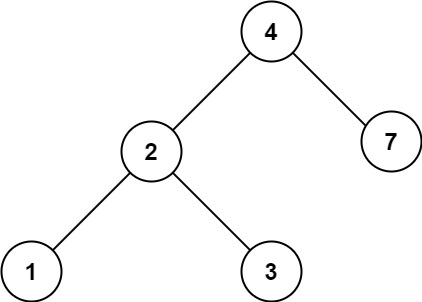
输入:root = [4,2,7,1,3], val = 5 输出:[]
提示:
- 数中节点数在
[1, 5000]范围内 1 <= Node.val <= 107root是二叉搜索树1 <= val <= 107
广度优先搜索
嘿嘿,很简单就做出来了。
if (!root) return nullptr; queue<TreeNode*> q; q.push(root); while (!q.empty()) { auto node = q.front(); if (node->val == val) return node; if (node->left) q.push(node->left); if (node->right) q.push(node->right); q.pop(); } return nullptr;
二叉搜索树满足如下性质:
- 左子树所有节点的元素值均小于根的元素值;
- 右子树所有节点的元素值均大于根的元素值。
递归
if (!root) return nullptr; if(root->val == val) return root; return (val < root->val) ? searchBST(root->left, val) : searchBST(root->right, val);
迭代
TreeNode* searchBST(TreeNode* root, int val) { while (root) { if (root->val == val) return root; root = (val < root->val) ? root->left : root->right; } return nullptr; }
701. 二叉搜索树中的插入操作
难度中等271
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:

输入:root = [4,2,7,1,3], val = 5 输出:[4,2,7,1,3,5] 解释:另一个满足题目要求可以通过的树是:
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25 输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5 输出:[4,2,7,1,3,5]
提示:
- 树中的节点数将在
[0, 104]的范围内。 -108 <= Node.val <= 108- 所有值
Node.val是 独一无二 的。 -108 <= val <= 108- 保证
val在原始BST中不存在。
如果该子树不为空,则问题转化成了将 val 插入到对应子树上。
否则,在此处新建一个以 val 为值的节点,并链接到其父节点root 上。
迭代
TreeNode* insertIntoBST(TreeNode* root, int val) { if (!root) return new TreeNode(val); TreeNode* pos = root; while (pos) { if (val < pos->val) { if (pos->left) pos = pos->left; else { pos->left = new TreeNode(val); break; } } else { if (pos->right) pos = pos->right; else { pos->right = new TreeNode(val); break; } } } return root; }
DAY14 二叉搜索树
98. 验证二叉搜索树
难度中等1443
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:

输入:root = [2,1,3] 输出:true
示例 2:

输入:root = [5,1,4,null,null,3,6] 输出:false 解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
- 树中节点数目范围在
[1, 104]内 -231 <= Node.val <= 231 - 1
思路:中序遍历二叉树,遍历完是数组是从小到大的。
void inorder(TreeNode* root, vector<int>& res) { if (root == nullptr) return; inorder(root->left, res); res.push_back(root->val); inorder(root->right, res); } bool isValidBST(TreeNode* root) { if (!root) return true; vector<int> res; inorder(root, res); for (int i = 0; i < res.size() - 1; i++) { if (res[i] > res[i + 1]) return false; } return true; }
653. 两数之和 IV - 输入 BST
难度简单318
给定一个二叉搜索树 root 和一个目标结果 k,如果 BST 中存在两个元素且它们的和等于给定的目标结果,则返回 true。
示例 1:

输入: root = [5,3,6,2,4,null,7], k = 9 输出: true
示例 2:

输入: root = [5,3,6,2,4,null,7], k = 28 输出: false
提示:
- 二叉树的节点个数的范围是
[1, 104]. -104 <= Node.val <= 104root为二叉搜索树-105 <= k <= 105
思路:随便用一种遍历方式把二叉树里的节点值都存进数组,然后用哈希表去找两数之和。
void inorder(TreeNode* root, vector<int>& res) { if (root == nullptr) return; inorder(root->left, res); res.push_back(root->val); inorder(root->right, res); } bool findTarget(TreeNode* root, int target) { if (!root) return false; vector<int> nums; inorder(root, nums); unordered_set<int> hashtable; for (int i = 0; i < nums.size(); i++) { //auto it即可 auto it = hashtable.find(target - nums[i]); if (it != hashtable.end()) return true; hashtable.insert(nums[i]); } return false; }
235. 二叉搜索树的最近公共祖先
难度简单783
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6 解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 输出: 2 解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
法一:二次遍历。就写一个从根节点到达pq节点路径的函数,两条路径中的最后一个相同节点就是最近公共祖先。
vector<TreeNode*> search(TreeNode* root, TreeNode* p) { vector<TreeNode*> path; TreeNode* cur = root; while (1) { if (p->val < cur->val) { path.push_back(cur); cur = cur->left; } else if(p->val > cur->val) { path.push_back(cur); cur = cur->right; } else { path.push_back(cur); break; } } return path; } TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { vector<TreeNode*> p1 = search(root, p); vector<TreeNode*> q1 = search(root, q); TreeNode* ancestor ; for (int i = 0; i < p1.size() && i < q1.size(); i++) { if (p1[i] == q1[i]) ancestor = p1[i]; else break; } return ancestor; }
法二:一次遍历。如果当前节点同时大于pq节点,那么pq就在左子树上,当前节点同时小于pq节点,则迭代到右子树;否则就是最近公共祖先。
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { TreeNode* cur = root; while (1) { if (cur->val > p->val && cur->val > q->val) cur = cur->left; else if (cur->val < p->val && cur->val < q->val) cur = cur->right; else break; } return cur; }
DAY15 数组
136. 只出现一次的数字
难度简单2305
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1] 输出: 1
示例 2:
输入: [4,1,2,1,2] 输出: 4
我的思路:简单的用哈希表对数组遍历两次,但时间和空间都用得挺多的。
int singleNumber(vector<int>& nums) { unordered_map<int, int> hashtable; for (auto x : nums) hashtable[x]++; for (auto x : nums) if (hashtable[x] == 1) return x; return 0; }
题解:由于题目中说其他的重复数字都是出现两次,故可以使用异或的性质,将数组中所有的元素进行异或运算,最后得到的结果就是只出现一次的数字。
int singleNumber(vector<int>& nums) { int res=0; for (auto x : nums) res ^= x; return res; }
169. 多数元素
难度简单1348
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:[3,2,3] 输出:3
示例 2:
输入:[2,2,1,1,1,2,2] 输出:2
我的思路:记录下出现次数最多的次数。
unordered_map<int, int> hashtable; int maxcout = 0; for (auto x : nums) { hashtable[x]++; maxcout = max(hashtable[x], maxcout); } for (auto x : nums) if (hashtable[x] == maxcout) return x; return 0;
题解:由于题目中说明的多数元素的个数大于n/2,所以可以排序完再返回nums[n/2]。
int majorityElement(vector<int>& nums) { sort(nums.begin(), nums.end()); return nums[nums.size() / 2]; }
15. 三数之和
难度中等4464
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]]
示例 2:
输入:nums = [] 输出:[]
示例 3:
输入:nums = [0] 输出:[]
思路:排序+双指针
vector<vector<int>> twoSum(vector<int>& nums, int start, int end, int target, int value) { vector<vector<int>> answer; while (start < end) { int sum = nums[start] + nums[end]; if (sum == target) { answer.push_back({value,nums[start],nums[end]}); while (start < end && nums[start] == nums[start + 1]) start++; start++; while (start < end && nums[end] == nums[end - 1]) end--; end--; } else if (sum < target) start++; else end--; } return answer; } vector<vector<int>> threeSum(vector<int>& nums) { vector<vector<int>> answer; int n = nums.size(); sort(nums.begin(), nums.end()); for (int i = 0; i < n; i++) { if (i > 0 && nums[i] == nums[i - 1]) continue; auto result = twoSum(nums, i + 1, n - 1, -nums[i], nums[i]); answer.insert(answer.end(), result.begin(), result.end()); } return answer; }
18. 四数之和
难度中等1156
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复):
0 <= a, b, c, d < na、b、c和d互不相同nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按 任意顺序 返回答案 。
示例 1:
输入:nums = [1,0,-1,0,-2,2], target = 0 输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
示例 2:
输入:nums = [2,2,2,2,2], target = 8 输出:[[2,2,2,2]]
思路好像就是比三数之和多加了一层循环。
vector<vector<int>> fourSum(vector<int>& nums, int target) { vector<vector<int>> quadruplets; if (nums.size() < 4) { return quadruplets; } sort(nums.begin(), nums.end()); int length = nums.size(); for (int i = 0; i < length - 3; i++) { if (i > 0 && nums[i] == nums[i - 1]) continue; //如果前四个数相加就大于目标值,那么后面更大的数相加也没机会等于target if ((long)nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target) break; //如果当前值加上最后三个数字还比目标值小,那么直接i++ if ((long)nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target) continue; for (int j = i + 1; j < length - 2; j++) { if (j > i + 1 && nums[j] == nums[j - 1]) continue; if ((long)nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target) break; if ((long)nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target) continue; int left = j + 1, right = length - 1; while (left < right) { int sum = nums[i] + nums[j] + nums[left] + nums[right]; if (sum == target) { quadruplets.push_back({ nums[i], nums[j], nums[left], nums[right] }); while (left < right && nums[left] == nums[left + 1]) left++; left++; while (left < right && nums[right] == nums[right - 1]) right--; right--; } else if (sum < target) { left++; } else { right--; } } } } return quadruplets; }
DAY16 数组
75. 颜色分类
难度中等1189
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库的sort函数的情况下解决这个问题。
示例 1:
输入:nums = [2,0,2,1,1,0] 输出:[0,0,1,1,2,2]
示例 2:
输入:nums = [2,0,1] 输出:[0,1,2]
提示:
n == nums.length1 <= n <= 300nums[i]为0、1或2
56. 合并区间
难度中等1372
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]] 解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]] 输出:[[1,5]] 解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
vector<vector<int>> merge(vector<vector<int>>& intervals) { if (intervals.size() == 0) return {}; //先对数组中的左区间进行排序 sort(intervals.begin(), intervals.end()); vector<vector<int>> merged; for (int i = 0; i < intervals.size(); ++i) { int L = intervals[i][0], R = intervals[i][1]; //如果merged为空或者merged的右边界小于当前区间的左界 if (!merged.size() || merged.back()[1] < L) { merged.push_back({L, R}); } else { //如果merged的右边界大于等于当前区间的左界 //那么merged的右边界就是右边界和当前有界的最大值 merged.back()[1] = max(merged.back()[1], R); } } return merged; }
705. 设计哈希集合
难度简单220
不使用任何内建的哈希表库设计一个哈希集合(HashSet)。
实现 MyHashSet 类:
void add(key)向哈希集合中插入值key。bool contains(key)返回哈希集合中是否存在这个值key。void remove(key)将给定值key从哈希集合中删除。如果哈希集合中没有这个值,什么也不做。
示例:
输入: ["MyHashSet", "add", "add", "contains", "contains", "add", "contains", "remove", "contains"] [[], [1], [2], [1], [3], [2], [2], [2], [2]] 输出: [null, null, null, true, false, null, true, null, false] 解释: MyHashSet myHashSet = new MyHashSet(); myHashSet.add(1); // set = [1] myHashSet.add(2); // set = [1, 2] myHashSet.contains(1); // 返回 True myHashSet.contains(3); // 返回 False ,(未找到) myHashSet.add(2); // set = [1, 2] myHashSet.contains(2); // 返回 True myHashSet.remove(2); // set = [1] myHashSet.contains(2); // 返回 False ,(已移除)
提示:
0 <= key <= 106- 最多调用
104次add、remove和contains
#include<vector> #include<list> using namespace std; class MyHashSet { private: vector<list<int>> data; static const int base = 769; static int hash(int key) { return key % base; } public: MyHashSet() : data(base) {} void add(int key) { int h = hash(key); for (auto it = data[h].begin(); it != data[h].end(); it++) if ((*it) == key) return; data[h].push_back(key); } void remove(int key) { int h = hash(key); for (auto it = data[h].begin(); it != data[h].end(); it++) { if ((*it) == key) { data[h].erase(it); return; } } } bool contains(int key) { int h = hash(key); for (auto it = data[h].begin(); it != data[h].end(); it++) { if ((*it) == key) { return true; } } return false; } };
706. 设计哈希映射
难度简单279
不使用任何内建的哈希表库设计一个哈希映射(HashMap)。
实现 MyHashMap 类:
MyHashMap()用空映射初始化对象void put(int key, int value)向 HashMap 插入一个键值对(key, value)。如果key已经存在于映射中,则更新其对应的值value。int get(int key)返回特定的key所映射的value;如果映射中不包含key的映射,返回-1。void remove(key)如果映射中存在key的映射,则移除key和它所对应的value。
示例:
输入: ["MyHashMap", "put", "put", "get", "get", "put", "get", "remove", "get"] [[], [1, 1], [2, 2], [1], [3], [2, 1], [2], [2], [2]] 输出: [null, null, null, 1, -1, null, 1, null, -1] 解释: MyHashMap myHashMap = new MyHashMap(); myHashMap.put(1, 1); // myHashMap 现在为 [[1,1]] myHashMap.put(2, 2); // myHashMap 现在为 [[1,1], [2,2]] myHashMap.get(1); // 返回 1 ,myHashMap 现在为 [[1,1], [2,2]] myHashMap.get(3); // 返回 -1(未找到),myHashMap 现在为 [[1,1], [2,2]] myHashMap.put(2, 1); // myHashMap 现在为 [[1,1], [2,1]](更新已有的值) myHashMap.get(2); // 返回 1 ,myHashMap 现在为 [[1,1], [2,1]] myHashMap.remove(2); // 删除键为 2 的数据,myHashMap 现在为 [[1,1]] myHashMap.get(2); // 返回 -1(未找到),myHashMap 现在为 [[1,1]]
提示:
0 <= key, value <= 106- 最多调用
104次put、get和remove方法
#include<vector> #include<list> using namespace std; class MyHashMap { private: vector<list<pair<int,int>>> data; static const int base = 769; static int hash(int key) { return key % base; } public: MyHashMap() : data(base) {} void put(int key, int value) { int h = hash(key); for (auto it = data[h].begin(); it != data[h].end(); it++) { if ((*it).first == key) { (*it).second = value; return; } } data[h].push_back(make_pair(key,value)); } int get(int key) { int h = hash(key); for (auto it = data[h].begin(); it != data[h].end(); it++) { if ((*it).first == key) { return (*it).second; } } return -1; } void remove(int key) { int h = hash(key); for (auto it = data[h].begin(); it != data[h].end(); it++) { if ((*it).first == key) { data[h].erase(it); return; } } } };
DAY17 数组
119. 杨辉三角 II
难度简单375
给定一个非负索引 rowIndex,返回「杨辉三角」的第 rowIndex 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。

示例 1:
输入: rowIndex = 3 输出: [1,3,3,1]
示例 2:
输入: rowIndex = 0 输出: [1]
示例 3:
输入: rowIndex = 1 输出: [1,1]
提示:
0 <= rowIndex <= 33
vector<int> getRow(int rowIndex) { //设置一个大小为rowIndex的二维数组 vector<vector<int>> C(rowIndex + 1); for (int i = 0; i <= rowIndex; ++i) { //数组的第i行设置为i+1个元素 C[i].resize(i + 1); //头元素和尾元素都设置为1 C[i][0] = C[i][i] = 1; for (int j = 1; j < i; ++j) { C[i][j] = C[i - 1][j - 1] + C[i - 1][j]; } } return C[rowIndex]; }
48. 旋转图像
难度中等1211
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:

输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
法一:找到规律,发现旋转后第 i 行第 j 列变成第 j 行第倒数第 i 列。
void rotate(vector<vector<int>>& matrix) { int m=matrix.size(); auto mat_new=matrix; for(int i=0;i<m;i++) { for(int j=0;j<m;j++) { mat_new[j][m-i-1]=matrix[i][j]; } } matrix=mat_new; }
法二:原地旋转。简单来说就是四个角互转。解题方法就是找到法一的旋转函数,将其四次代入,然后逆序。
void rotate(vector<vector<int>>& matrix) { int n = matrix.size(); for (int i = 0; i < n / 2; ++i) { for (int j = 0; j < (n + 1) / 2; ++j) { int temp = matrix[i][j]; matrix[i][j] = matrix[n - j - 1][i]; matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1]; matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1]; matrix[j][n - i - 1] = temp; } } }
法三:发现可以水平翻转再主对角线翻转即可得到结果。也可以用法一的递推式证明此解法。
void rotate(vector<vector<int>>& matrix) { int n = matrix.size(); for (int i = 0; i < n / 2; ++i) { for (int j = 0; j < (n + 1) / 2; ++j) { int temp = matrix[i][j]; matrix[i][j] = matrix[n - j - 1][i]; matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1]; matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1]; matrix[j][n - i - 1] = temp; } } }
59. 螺旋矩阵 II
难度中等634
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:

输入:n = 3 输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1 输出:[[1]]
提示:
1 <= n <= 20
DAY18 数组
240. 搜索二维矩阵 II
难度中等956
编写一个高效的算法来搜索 *m* x *n* 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例 1:

输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 输出:true
示例 2:
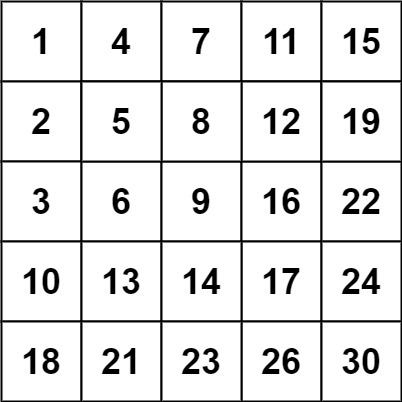
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- 每行的所有元素从左到右升序排列
- 每列的所有元素从上到下升序排列
-109 <= target <= 109
思路:从中间开始遍历,当前比target大就向左,比target小就向下。
bool searchMatrix(vector<vector<int>>& matrix, int target) { int m=matrix.size(); int n=matrix[0].size(); int i=0,j=n-1; while(i<m&&j>=0) { if(target==matrix[i][j]) return true; else if(target>matrix[i][j]) i++; else j--; } return false; }
435. 无重叠区间
难度中等629
给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。
示例 1:
输入: intervals = [[1,2],[2,3],[3,4],[1,3]] 输出: 1 解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: intervals = [ [1,2], [1,2], [1,2] ] 输出: 2 解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
输入: intervals = [ [1,2], [2,3] ] 输出: 0 解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
思路:题目等价于「选出最多数量的区间,使得它们互不重叠」。如何寻找第一个区间,我们会发现第一个区间是右端点最小的那个区间。即使有多个区间右端点同样的最小,我们也只需要取其中一个区间即可。
贪心算法
int eraseOverlapIntervals(vector<vector<int>>& intervals) { if (intervals.empty()) { return 0; } //将区间右端点进行从小到大排序 sort(intervals.begin(), intervals.end(), [](const auto& u, const auto& v) { return u[1] < v[1]; }); int n = intervals.size(); int right = intervals[0][1]; int ans = 1; for (int i = 1; i < n; ++i) { //如果遍历到的这个区间左端点大于等于上个区间的右端点,那么就是一个新区间 if (intervals[i][0] >= right) { ++ans; right = intervals[i][1]; } } return n - ans; }
贪心算法
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择。
算法思路
贪心算法一般按如下步骤进行:
- ①建立数学模型来描述问题 。
- ②把求解的问题分成若干个子问题 。
- ③对每个子问题求解,得到子问题的局部最优解 。
- ④把子问题的解局部最优解合成原来解问题的一个解 。
贪心选择性质
一个问题的整体最优解可通过一系列局部的最优解的选择达到,并且每次的选择可以依赖以前作出的选择,但不依赖于后面要作出的选择。这就是贪心选择性质。对于一个具体问题,要确定它是否具有贪心选择性质,必须证明每一步所作的贪心选择最终导致问题的整体最优解
DAY19 数组
238. 除自身以外数组的乘积
难度中等1091
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法,且在 O(*n*) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4] 输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3] 输出: [0,0,9,0,0]
提示:
2 <= nums.length <= 105-30 <= nums[i] <= 30- 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
思路:前缀之积乘以后缀之积就是结果。
vector<int> productExceptSelf(vector<int>& nums) { int length = nums.size(); // L 和 R 分别表示左右两侧的乘积列表 vector<int> L(length), R(length); vector<int> answer(length); // L[i] 为索引 i 左侧所有元素的乘积 // 对于索引为 '0' 的元素,因为左侧没有元素,所以 L[0] = 1 L[0] = 1; for (int i = 1; i < length; i++) L[i] = nums[i - 1] * L[i - 1]; // R[i] 为索引 i 右侧所有元素的乘积 // 对于索引为 'length-1' 的元素,因为右侧没有元素,所以 R[length-1] = 1 R[length - 1] = 1; for (int i = length - 2; i >= 0; i--) R[i] = nums[i + 1] * R[i + 1]; // 对于索引 i,除 nums[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积 for (int i = 0; i < length; i++) answer[i] = L[i] * R[i]; return answer; }
334. 递增的三元子序列
难度中等546
给你一个整数数组 nums ,判断这个数组中是否存在长度为 3 的递增子序列。
如果存在这样的三元组下标 (i, j, k) 且满足 i < j < k ,使得 nums[i] < nums[j] < nums[k] ,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [1,2,3,4,5] 输出:true 解释:任何 i < j < k 的三元组都满足题意
示例 2:
输入:nums = [5,4,3,2,1] 输出:false 解释:不存在满足题意的三元组
示例 3:
输入:nums = [2,1,5,0,4,6] 输出:true 解释:三元组 (3, 4, 5) 满足题意,因为 nums[3] == 0 < nums[4] == 4 < nums[5] == 6
贪心算法
可以使用贪心的方法将空间复杂度降到O(1)。从左到右遍历数组 nums,遍历过程中维护两个变量 first 和 second,分别表示递增的三元子序列中的第一个数和第二个数,任何时候都有first<second。
bool increasingTriplet(vector<int>& nums) { int n = nums.size(); if (n < 3) return false; int first = nums[0], second = INT_MAX; for (int i = 1; i < n; i++) { int num = nums[i]; if (num > second) return true; else if (num > first) second = num; else first = num; } return false; }
560. 和为 K 的子数组
难度中等1374
给你一个整数数组 nums 和一个整数 k ,请你统计并返回该数组中和为 k 的连续子数组的个数。
示例 1:
输入:nums = [1,1,1], k = 2 输出:2
示例 2:
输入:nums = [1,2,3], k = 3 输出:2
DAY20 字符串
415. 字符串相加
难度简单525
给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。
你不能使用任何內建的用于处理大整数的库(比如 BigInteger), 也不能直接将输入的字符串转换为整数形式。
示例 1:
输入:num1 = "11", num2 = "123" 输出:"134"
示例 2:
输入:num1 = "456", num2 = "77" 输出:"533"
示例 3:
输入:num1 = "0", num2 = "0" 输出:"0"
我的思路:将num12中的数字取出相加再转成字符串,但这道题这种方法通不过,因为num12中的数字可以有几十位,导致longlong类型都不够用。
string addStrings(string num1, string num2) { int m = num1.size(), n = num2.size(); int a = num1[0] - '0'; int b = num2[0] - '0'; for (int i = 1;i < m; i++) { int t = num1[i] - '0'; a = a * 10 + t; } for (int i = 1; i <n; i++) { int t = num2[i] - '0'; b = b * 10 + t; } return to_string(a + b); }
于是参考了一下题解,发现一位一位加比较合适。
string addStrings(string num1, string num2) { int i = num1.length() - 1, j = num2.length() - 1, add = 0; string ans ; while (i >= 0 || j >= 0 || add != 0) { int x = i >= 0 ? num1[i] - '0' : 0; int y = j >= 0 ? num2[j] - '0' : 0; int result = x + y + add; ans.push_back('0' + result % 10); add = result / 10; i--; j--; } // 计算完以后的答案需要翻转过来 reverse(ans.begin(), ans.end()); return ans; }
409. 最长回文串
难度简单389
给定一个包含大写字母和小写字母的字符串 s ,返回 通过这些字母构造成的 最长的回文串 。
在构造过程中,请注意 区分大小写 。比如 "Aa" 不能当做一个回文字符串。
示例 1:
输入:s = "abccccdd" 输出:7 解释: 我们可以构造的最长的回文串是"dccaccd", 它的长度是 7。
示例 2:
输入:s = "a" 输入:1
示例 3:
输入:s = "bb" 输入: 2
提示:
1 <= s.length <= 2000s只能由小写和/或大写英文字母组成
思路:回文中都是偶数个字符,只有最中间的可以是奇数字符。所以当某个元素有奇数个,且ans为偶数的情况下,ans可以加一。
int longestPalindrome(string s) { unordered_map<char, int> hashtable; for (auto x : s) { hashtable[x]++; } int ans = 0; for (auto x:hashtable) { ans += x.second / 2 * 2; if (x.second % 2 == 1 && ans % 2 == 0) ans++; } return ans; }
DAY21 字符串
290. 单词规律
难度简单443
给定一种规律 pattern 和一个字符串 s ,判断 s 是否遵循相同的规律。
这里的 遵循 指完全匹配,例如, pattern 里的每个字母和字符串 str 中的每个非空单词之间存在着双向连接的对应规律。
示例1:
输入: pattern = "abba", str = "dog cat cat dog" 输出: true
示例 2:
输入:pattern = "abba", str = "dog cat cat fish" 输出: false
示例 3:
输入: pattern = "aaaa", str = "dog cat cat dog" 输出: false
提示:
1 <= pattern.length <= 300pattern只包含小写英文字母1 <= s.length <= 3000s只包含小写英文字母和' 's不包含 任何前导或尾随对空格s中每个单词都被 单个空格 分隔
763. 划分字母区间
难度中等681
字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。
示例:
输入:S = "ababcbacadefegdehijhklij" 输出:[9,7,8] 解释: 划分结果为 "ababcbaca", "defegde", "hijhklij"。 每个字母最多出现在一个片段中。 像 "ababcbacadefegde", "hijhklij" 的划分是错误的,因为划分的片段数较少。
提示:
S的长度在[1, 500]之间。S只包含小写字母'a'到'z'。
DAY22 字符串
49. 字母异位词分组
难度中等1076
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的字母得到的一个新单词,所有源单词中的字母通常恰好只用一次。
示例 1:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"] 输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
示例 2:
输入: strs = [""] 输出: [[""]]
示例 3:
输入: strs = ["a"] 输出: [["a"]]
提示:
1 <= strs.length <= 1040 <= strs[i].length <= 100strs[i]仅包含小写字母
43. 字符串相乘
难度中等885
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
注意:不能使用任何内置的 BigInteger 库或直接将输入转换为整数。
示例 1:
输入: num1 = "2", num2 = "3" 输出: "6"
示例 2:
输入: num1 = "123", num2 = "456" 输出: "56088"
提示:
1 <= num1.length, num2.length <= 200num1和num2只能由数字组成。num1和num2都不包含任何前导零,除了数字0本身。
DAY23 字符串
187. 重复的DNA序列
难度中等355
DNA序列 由一系列核苷酸组成,缩写为 'A', 'C', 'G' 和 'T'.。
- 例如,
"ACGAATTCCG"是一个 DNA序列 。
在研究 DNA 时,识别 DNA 中的重复序列非常有用。
给定一个表示 DNA序列 的字符串 s ,返回所有在 DNA 分子中出现不止一次的 长度为 10 的序列(子字符串)。你可以按 任意顺序 返回答案。
示例 1:
输入:s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT" 输出:["AAAAACCCCC","CCCCCAAAAA"]
示例 2:
输入:s = "AAAAAAAAAAAAA" 输出:["AAAAAAAAAA"]
提示:
0 <= s.length <= 105s[i]``==``'A'、'C'、'G'or'T'
5. 最长回文子串
难度中等4971
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd" 输出:"bb"
DAY24 链表
2. 两数相加
难度中等7791
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
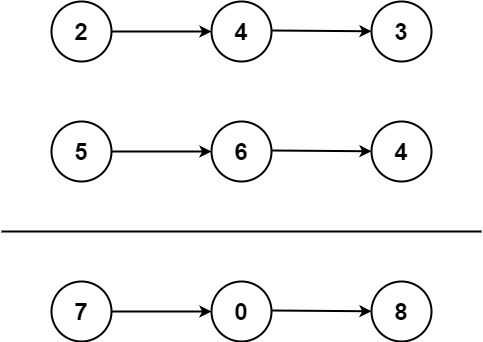
输入:l1 = [2,4,3], l2 = [5,6,4] 输出:[7,0,8] 解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0] 输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9] 输出:[8,9,9,9,0,0,0,1]
提示:
- 每个链表中的节点数在范围
[1, 100]内 0 <= Node.val <= 9- 题目数据保证列表表示的数字不含前导零
142. 环形链表 II
难度中等1494
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:

输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:

输入:head = [1,2], pos = 0 输出:返回索引为 0 的链表节点 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1 输出:返回 null 解释:链表中没有环。
提示:
- 链表中节点的数目范围在范围
[0, 104]内 -105 <= Node.val <= 105pos的值为-1或者链表中的一个有效索引
进阶:你是否可以使用 O(1) 空间解决此题?
DAY25 链表
160. 相交链表
难度简单1636
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal- 相交的起始节点的值。如果不存在相交节点,这一值为0listA- 第一个链表listB- 第二个链表skipA- 在listA中(从头节点开始)跳到交叉节点的节点数skipB- 在listB中(从头节点开始)跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构,并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例 1:
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3 输出:Intersected at '8' 解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。 从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。 在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 输出:Intersected at '2' 解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。 从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。 在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 输出:null 解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。 由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。 这两个链表不相交,因此返回 null 。
提示:
listA中节点数目为mlistB中节点数目为n1 <= m, n <= 3 * 1041 <= Node.val <= 1050 <= skipA <= m0 <= skipB <= n- 如果
listA和listB没有交点,intersectVal为0 - 如果
listA和listB有交点,intersectVal == listA[skipA] == listB[skipB]
进阶:你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案?
82. 删除排序链表中的重复元素 II
难度中等851
给定一个已排序的链表的头 head , 删除原始链表中所有重复数字的节点,只留下不同的数字 。返回 已排序的链表 。
示例 1:
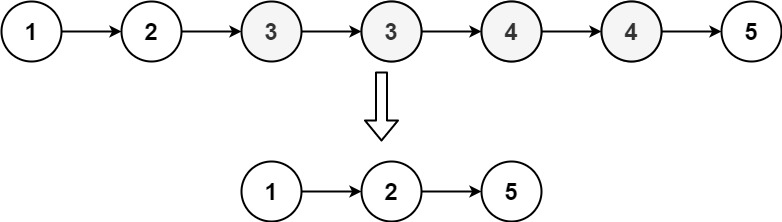
输入:head = [1,2,3,3,4,4,5] 输出:[1,2,5]
示例 2:
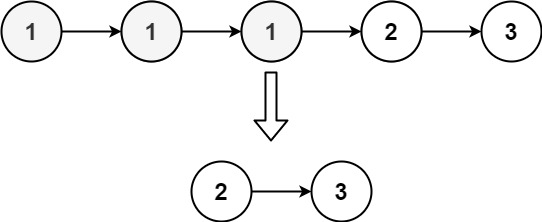
输入:head = [1,1,1,2,3] 输出:[2,3]
提示:
- 链表中节点数目在范围
[0, 300]内 -100 <= Node.val <= 100- 题目数据保证链表已经按升序 排列
通过次数237,056
提交次数444,867
DAY26 链表
24. 两两交换链表中的节点
难度中等1322
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:

输入:head = [1,2,3,4] 输出:[2,1,4,3]
示例 2:
输入:head = [] 输出:[]
示例 3:
输入:head = [1] 输出:[1]
提示:
- 链表中节点的数目在范围
[0, 100]内 0 <= Node.val <= 100
707. 设计链表
难度中等398
设计链表的实现。您可以选择使用单链表或双链表。单链表中的节点应该具有两个属性:val 和 next。val 是当前节点的值,next 是指向下一个节点的指针/引用。如果要使用双向链表,则还需要一个属性 prev 以指示链表中的上一个节点。假设链表中的所有节点都是 0-index 的。
在链表类中实现这些功能:
- get(index):获取链表中第
index个节点的值。如果索引无效,则返回-1。 - addAtHead(val):在链表的第一个元素之前添加一个值为
val的节点。插入后,新节点将成为链表的第一个节点。 - addAtTail(val):将值为
val的节点追加到链表的最后一个元素。 - addAtIndex(index,val):在链表中的第
index个节点之前添加值为val的节点。如果index等于链表的长度,则该节点将附加到链表的末尾。如果index大于链表长度,则不会插入节点。如果index小于0,则在头部插入节点。 - deleteAtIndex(index):如果索引
index有效,则删除链表中的第index个节点。
示例:
MyLinkedList linkedList = new MyLinkedList(); linkedList.addAtHead(1); linkedList.addAtTail(3); linkedList.addAtIndex(1,2); //链表变为1-> 2-> 3 linkedList.get(1); //返回2 linkedList.deleteAtIndex(1); //现在链表是1-> 3 linkedList.get(1); //返回3
提示:
- 所有
val值都在[1, 1000]之内。 - 操作次数将在
[1, 1000]之内。 - 请不要使用内置的 LinkedList 库。
DAY27 链表
25. K 个一组翻转链表
难度困难1562
给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。
k 是一个正整数,它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
进阶:
- 你可以设计一个只使用常数额外空间的算法来解决此问题吗?
- 你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
示例 1:
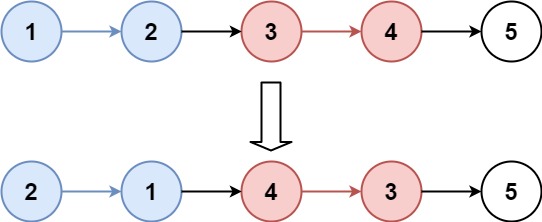
输入:head = [1,2,3,4,5], k = 2 输出:[2,1,4,3,5]
示例 2:
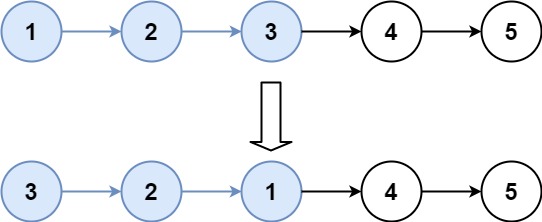
输入:head = [1,2,3,4,5], k = 3 输出:[3,2,1,4,5]
示例 3:
输入:head = [1,2,3,4,5], k = 1 输出:[1,2,3,4,5]
示例 4:
输入:head = [1], k = 1 输出:[1]
提示:
- 列表中节点的数量在范围
sz内 1 <= sz <= 50000 <= Node.val <= 10001 <= k <= sz
143. 重排链表
难度中等849
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例 1:
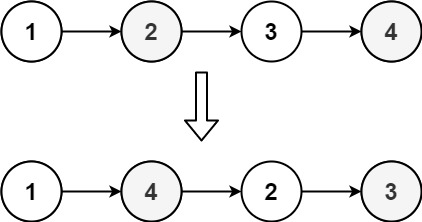
输入:head = [1,2,3,4] 输出:[1,4,2,3]
示例 2:
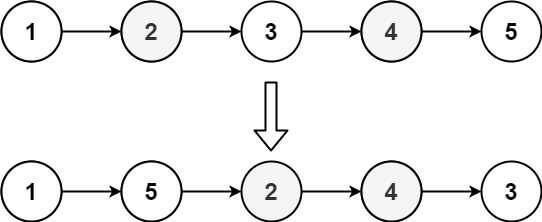
输入:head = [1,2,3,4,5] 输出:[1,5,2,4,3]
提示:
- 链表的长度范围为
[1, 5 * 104] 1 <= node.val <= 1000
DAY28 栈/队列
155. 最小栈
难度简单1245
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack()初始化堆栈对象。void push(int val)将元素val推入堆栈。void pop()删除堆栈顶部的元素。int top()获取堆栈顶部的元素。int getMin()获取堆栈中的最小元素。
示例 1:
输入: ["MinStack","push","push","push","getMin","pop","top","getMin"] [[],[-2],[0],[-3],[],[],[],[]] 输出: [null,null,null,null,-3,null,0,-2] 解释: MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.getMin(); --> 返回 -3. minStack.pop(); minStack.top(); --> 返回 0. minStack.getMin(); --> 返回 -2.
提示:
-231 <= val <= 231 - 1pop、top和getMin操作总是在 非空栈 上调用push,pop,top, andgetMin最多被调用3 * 104次
1249. 移除无效的括号
难度中等175
给你一个由 '('、')' 和小写字母组成的字符串 s。
你需要从字符串中删除最少数目的 '(' 或者 ')' (可以删除任意位置的括号),使得剩下的「括号字符串」有效。
请返回任意一个合法字符串。
有效「括号字符串」应当符合以下 任意一条 要求:
- 空字符串或只包含小写字母的字符串
- 可以被写作
AB(A连接B)的字符串,其中A和B都是有效「括号字符串」 - 可以被写作
(A)的字符串,其中A是一个有效的「括号字符串」
示例 1:
输入:s = "lee(t(c)o)de)" 输出:"lee(t(c)o)de" 解释:"lee(t(co)de)" , "lee(t(c)ode)" 也是一个可行答案。
示例 2:
输入:s = "a)b(c)d" 输出:"ab(c)d"
示例 3:
输入:s = "))((" 输出:"" 解释:空字符串也是有效的
提示:
1 <= s.length <= 105s[i]可能是'('、')'或英文小写字母
1823. 找出游戏的获胜者
难度中等42
共有 n 名小伙伴一起做游戏。小伙伴们围成一圈,按 顺时针顺序 从 1 到 n 编号。确切地说,从第 i 名小伙伴顺时针移动一位会到达第 (i+1) 名小伙伴的位置,其中 1 <= i < n ,从第 n 名小伙伴顺时针移动一位会回到第 1 名小伙伴的位置。
游戏遵循如下规则:
- 从第
1名小伙伴所在位置 开始 。 - 沿着顺时针方向数
k名小伙伴,计数时需要 包含 起始时的那位小伙伴。逐个绕圈进行计数,一些小伙伴可能会被数过不止一次。 - 你数到的最后一名小伙伴需要离开圈子,并视作输掉游戏。
- 如果圈子中仍然有不止一名小伙伴,从刚刚输掉的小伙伴的 顺时针下一位 小伙伴 开始,回到步骤
2继续执行。 - 否则,圈子中最后一名小伙伴赢得游戏。
给你参与游戏的小伙伴总数 n ,和一个整数 k ,返回游戏的获胜者。
示例 1:
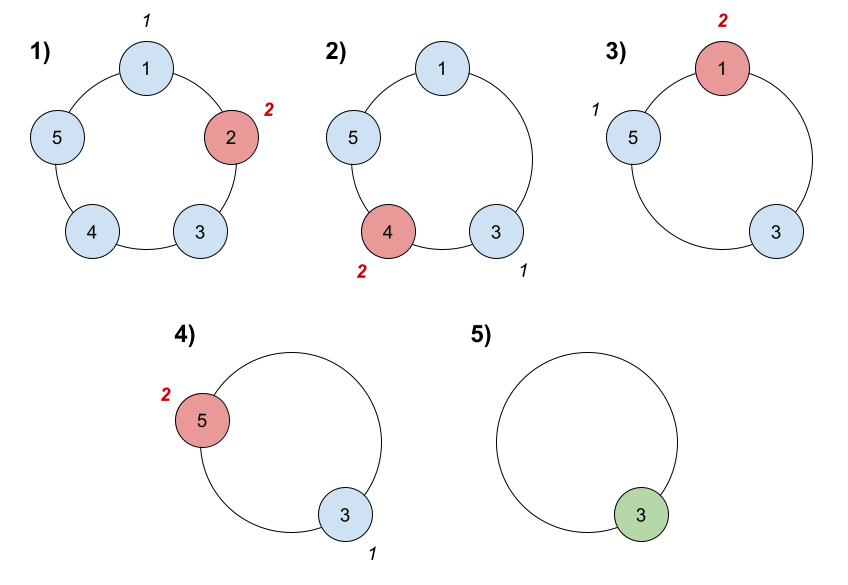
输入:n = 5, k = 2 输出:3 解释:游戏运行步骤如下: 1) 从小伙伴 1 开始。 2) 顺时针数 2 名小伙伴,也就是小伙伴 1 和 2 。 3) 小伙伴 2 离开圈子。下一次从小伙伴 3 开始。 4) 顺时针数 2 名小伙伴,也就是小伙伴 3 和 4 。 5) 小伙伴 4 离开圈子。下一次从小伙伴 5 开始。 6) 顺时针数 2 名小伙伴,也就是小伙伴 5 和 1 。 7) 小伙伴 1 离开圈子。下一次从小伙伴 3 开始。 8) 顺时针数 2 名小伙伴,也就是小伙伴 3 和 5 。 9) 小伙伴 5 离开圈子。只剩下小伙伴 3 。所以小伙伴 3 是游戏的获胜者。
示例 2:
输入:n = 6, k = 5 输出:1 解释:小伙伴离开圈子的顺序:5、4、6、2、3 。小伙伴 1 是游戏的获胜者。
提示:
1 <= k <= n <= 500
DAY29 树
108. 将有序数组转换为二叉搜索树
难度简单981
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:

输入:nums = [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:

输入:nums = [1,3] 输出:[3,1] 解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本