TZOJ 挑战题库随机训练03
A.Unique Encryption Keys回到顶部
题意
m([1,10^6])个数a[i]([0,2^30]),q([0,10^6])次询问,每次询问区间[L,R]是否存在相同的数字
题解
思考一个问题,令pre[i]为值为i的前一个数字的位置
询问区间[L,R]相当于区间内的所有数,pre[a[i]]都在外面即pre[a[i]]<l则合法OK
转化一下,相当于区间内max(pre[a[i]])<l
令f[i]为[1,i]出现重复数的最大位置,那么可以推出f[i]=max(f[i-1],pre[a[i]])
那么答案就是f[r]<l?OK:Error,复杂度O(nlogn)
PS:卡了一下常数,把unordered_map改成离散化,内存少了1倍,时间快了1.5倍

代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=1e6+5; 4 int a[N],b[N],pre[N]; 5 bool ans[N]; 6 struct node{ 7 int l,r,id; 8 bool operator<(const node &d)const{ 9 return r<d.r||(r==d.r&&l<d.l); 10 } 11 }q[N]; 12 inline int read() { 13 char ch = getchar(); int x = 0, f = 1; 14 while(ch < '0' || ch > '9') { 15 if(ch == '-') f = -1; 16 ch = getchar(); 17 } while('0' <= ch && ch <= '9') { 18 x = x * 10 + ch - '0'; 19 ch = getchar(); 20 } return x * f; 21 } 22 int main(){ 23 int n,m; 24 while(scanf("%d%d",&n,&m)!=EOF,n||m){ 25 for(int i=1;i<=n;i++){ 26 a[i]=read(); 27 b[i]=a[i]; 28 } 29 sort(b+1,b+1+n); 30 int sz=unique(b+1,b+1+n)-b-1; 31 for(int i=1;i<=sz;i++)pre[i]=0; 32 for(int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+1+sz,a[i])-b; 33 for(int i=1;i<=m;i++){ 34 q[i].l=read();q[i].r=read(); 35 q[i].id=i; 36 } 37 sort(q+1,q+1+m); 38 int p=1,r=0; 39 for(int i=1;p<=m&&i<=n+1;i++){ 40 while(p<=m&&i>q[p].r)ans[q[p].id]=(r<q[p].l),p++; 41 if(pre[a[i]])r=max(r,pre[a[i]]); 42 pre[a[i]]=i; 43 } 44 for(int i=1;i<=m;i++)printf("%s\n",ans[i]?"OK":"Error"); 45 puts(""); 46 } 47 return 0; 48 }

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=1e6+5; 4 int f[N]; 5 unordered_map<int,int>pre; 6 inline int read() { 7 char ch = getchar(); int x = 0, f = 1; 8 while(ch < '0' || ch > '9') { 9 if(ch == '-') f = -1; 10 ch = getchar(); 11 } while('0' <= ch && ch <= '9') { 12 x = x * 10 + ch - '0'; 13 ch = getchar(); 14 } return x * f; 15 } 16 int main(){ 17 int n,m,x,l,r; 18 while(scanf("%d%d",&n,&m)!=EOF,n||m){ 19 pre.clear(); 20 for(int i=1;i<=n;i++)f[i]=0; 21 for(int i=1;i<=n;i++){ 22 x=read(); 23 f[i]=max(f[i-1],pre[x]); 24 pre[x]=i; 25 } 26 for(int i=1;i<=m;i++){ 27 l=read();r=read(); 28 printf("%s\n",f[r]<l?"OK":"Error"); 29 } 30 puts(""); 31 } 32 return 0; 33 }
B.奇数阶魔方(II)回到顶部
题意
给一个奇数n([3,21]),输出一个n*n的矩阵使得每行每列和对角线都相等
题解
复杂做法:把模仿旋转45°,然后构造,再转回来,复杂度O(n^2)
简单做法见下图,相当于(x+1)%n,(y+1)%n,到最后(x+1)%n+1
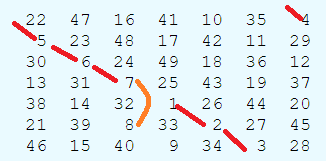
代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 int n,a[22][22]; 6 while(scanf("%d",&n)!=EOF,n) 7 { 8 int s=1,x=n/2+2,y=n/2+1; 9 a[x][y]=s++; 10 while(s<=n*n){ 11 if(s%n==1)x=(x+1)%n+1; 12 else x=x%n+1,y=y%n+1; 13 a[x][y]=s++; 14 } 15 for(int i=1;i<=n;i++){ 16 for(int j=1;j<=n;j++) 17 printf("%4d",a[i][j]); 18 puts(""); 19 } 20 } 21 return 0; 22 }

1 #include<bits/stdc++.h> 2 using namespace std; 3 4 int out[44][22],ans[22][22]; 5 int main(){ 6 int n; 7 while(cin>>n,n){ 8 // 1//3 9 // 2//20 16 10 // 3//7 8 9 11 // 4//24 25 21 22 12 // 5//11 12 13 14 15 13 // 6//4 5 1 2 14 // 7//17 18 19 15 // 8//10 6 16 // 9//23 17 for(int i=1;i<=n;i++)out[n][i]=(n*n+1)/2-n/2+i-1; 18 int p=1,up=(2*n-(n+1))/2; 19 for(int i=n+1;i<n*2;i+=2){ 20 for(int j=1;j<=up;j++)out[i][up+j]=p++; 21 for(int j=1;j<=n-2*up;j++)out[i-n][j]=p++; 22 for(int j=1;j<=up;j++)out[i][j]=p++; 23 up--; 24 } 25 p+=n; 26 up=1; 27 for(int i=2;i<n;i+=2){ 28 for(int j=1;j<=up;j++)out[i][up+j]=p++; 29 for(int j=1;j<=n-2*up;j++)out[i+n][j]=p++; 30 for(int j=1;j<=up;j++)out[i][j]=p++; 31 up++; 32 } 33 for(int i=1;i<=n;i++){ 34 int px=1,py=n-i+1; 35 for(int j=1;j<=i;j++){ 36 ans[px][py]=out[i][j]; 37 px++,py++; 38 } 39 } 40 for(int i=n+1;i<2*n;i++){ 41 int px=i-n+1,py=1; 42 for(int j=1;j<=2*n-i;j++){ 43 ans[px][py]=out[i][j]; 44 px++,py++; 45 } 46 } 47 for(int i=1;i<=n;i++){ 48 for(int j=1;j<=n;j++) 49 printf("%4d",ans[i][j]); 50 printf("\n"); 51 } 52 } 53 return 0; 54 }
C.Graph’s Cycle Component回到顶部
题意
n([1,10^5))个点m([1,3*10^5])条边的无向图,问有多少个连通图和连通图是环图的数量
题解
连通图很好求,并查集求一下
环图怎么求呢?首先如果是环图,那么图中的每个点只会连2条边,也就是in[u]=2
如果in[u]!=2那么该连通图不合法,也就需要通过并查集找到u的父亲,置f[f[u]]=0
注意这里是f[f[u]]而不是f[u],因为f[u]指向的值才是父亲
复杂度O(mlogn)
代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 4 const int N=1e5+5; 5 int n,m; 6 int f[N],in[N]; 7 int find(int x){ 8 return f[x]==x?x:f[x]=find(f[x]); 9 } 10 int main(){ 11 while(scanf("%d%d",&n,&m)!=EOF,n||m){ 12 for(int i=1;i<=n;i++)f[i]=i,in[i]=0; 13 for(int i=1;i<=m;i++){ 14 int u,v; 15 scanf("%d%d",&u,&v); 16 u++,v++; 17 in[u]++,in[v]++; 18 int fu=find(u); 19 int fv=find(v); 20 if(fu!=fv) 21 f[fu]=fv; 22 } 23 int cnt=0,ok=0; 24 for(int i=1;i<=n;i++)f[i]=find(i); 25 for(int i=1;i<=n;i++)if(f[i]==i)cnt++; 26 for(int i=1;i<=n;i++)if(in[i]!=2)f[find(i)]=0; 27 for(int i=1;i<=n;i++)if(f[i]==i)ok++; 28 printf("%d %d\n",cnt,ok); 29 } 30 return 0; 31 }
D.Lowest Bit回到顶部
题意
给一个数A([1,100]),求二进制中最后1个1所代表的大小
题解
求出A的二进制,复杂度O(logn)
代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 int main(){ 4 int x; 5 while(scanf("%d",&x)!=EOF,x){ 6 int val=1; 7 do{ 8 if(x&1)break; 9 val<<=1; 10 x>>=1; 11 }while(x); 12 printf("%d\n",val); 13 } 14 return 0; 15 }
E.Divide and Count回到顶部
题意
n个盒子,每个盒子可以放a[i]个球,现在有Σa个球,问有多少不同的方法。保证所有正整数<=12并且答案在32位数之内
题解
令sum为还剩多少球
第一个盒子可以放a[1]个球,方案数C(sum,a[1])
第二个盒子可以放a[2]个球,方案数C(sum-a[1],a[2])
以此类推
注意最后需要把相同的除掉,复杂度O(Σa)
代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 4 #define LL long long 5 LL C(int n,int m){ 6 LL sum=1; 7 if(m>n/2)m=n-m; 8 for(int i=1;i<=m;i++) 9 sum=sum*(n-i+1)/i; 10 return sum; 11 } 12 int main(){ 13 int n,fac[13]={1,1}; 14 for(int i=2;i<=12;i++)fac[i]=fac[i-1]*i; 15 while(scanf("%d",&n)!=EOF){ 16 int cnt[13]={0},a[13],sum=0; 17 for(int i=1;i<=n;i++){ 18 scanf("%d",&a[i]); 19 cnt[a[i]]++; 20 sum+=a[i]; 21 } 22 LL ans=1; 23 for(int i=1;i<n;i++){ 24 ans=ans*C(sum,a[i]); 25 sum-=a[i]; 26 } 27 for(int i=1;i<=12;i++)ans/=fac[cnt[i]]; 28 printf("%lld\n",ans); 29 } 30 return 0; 31 }
F.过山车回到顶部
题意
n([1,500])个男生,m([1,500])个女生,k([1,1000])对匹配,问男生和女生最多可以匹配出多少对
题解
匈牙利算法模板,复杂度O(max(n,m)k)
代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=505; 4 int k,m,n; 5 int G[N][N],vis[N],match[N];//给男生匹配女生 6 int Find(int x) 7 { 8 for(int i=1;i<=n;i++)//男生 9 { 10 if(G[x][i]&&!vis[i]) 11 { 12 vis[i]=1; 13 if(match[i]==-1||Find(match[i])) 14 { 15 match[i]=x; 16 return 1; 17 } 18 } 19 } 20 return 0; 21 } 22 int main() 23 { 24 while(scanf("%d",&k)!=EOF,k) 25 { 26 memset(G,0,sizeof(G)); 27 scanf("%d%d",&m,&n); 28 for(int i=0;i<k;i++) 29 { 30 int boy,girl; 31 scanf("%d%d",&girl,&boy); 32 G[girl][boy]=1; 33 } 34 memset(match,-1,sizeof(match)); 35 int ans=0; 36 for(int i=1;i<=m;i++)//女生 37 { 38 memset(vis,0,sizeof(vis)); 39 if(Find(i))ans++; 40 } 41 printf("%d\n",ans); 42 } 43 return 0; 44 }
G.The Magic Bus回到顶部
题意
Brian第m([0,60))分钟到0车站,给你一张发车表,每小时都一样,Brian到车站i,坐最快发车的车到下一站i+1,问当Brian到车站n([1,10^9))的时候,它坐的是几路车
保证不存在同一时间发车,发车表大小不超过20
题解
由于发车表大小不超过20,那么一定存在不超过20的循环,求出循环节大小后即可,复杂度O(20log20)
细节:由于是到n,所以实际求的是n-1坐什么车
PS:Brian要去第10^9个车站有点狠
代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 4 vector<pair<int,int>>vec;//time bus_id 5 map<pair<int,int>,int>ma; 6 int main(){ 7 int n,bus,x,m_ti,pos,ca=1; 8 while(scanf("%d",&n)!=EOF,n){ 9 vec.clear(); 10 ma.clear(); 11 for(int i=1;i<=n;i++){ 12 scanf("%d:",&bus); 13 while(1){ 14 scanf("%d",&x); 15 if(x==-1)break; 16 vec.push_back({x,bus}); 17 } 18 } 19 sort(vec.begin(),vec.end()); 20 scanf("%d%d",&m_ti,&pos); 21 int r=0; 22 vector<int>road; 23 for(int i=0;i<vec.size();i++) 24 if(vec[i].first>=m_ti){ 25 r=i; 26 break; 27 } 28 road.push_back(vec[r].second); 29 ma[vec[r]]=1; 30 while(1){ 31 if(ma.size()>=pos)break; 32 r=(r+1)%vec.size(); 33 if(ma.count(vec[r]))break; 34 ma[vec[r]]=1; 35 road.push_back(vec[r].second); 36 } 37 int kpos=(ma.size()>=pos?pos-1:(pos-1)%ma.size()); 38 printf("Case %d: Brian arrives at stop %d by bus %d.\n",ca++,pos,road[kpos]); 39 } 40 return 0; 41 }
H.Counting Leaves回到顶部
题意
给一颗树,求每一层叶子节点的个数
题解
需要注意当N<=0||N>=100的时候不要越界,然后直接输出0,复杂度O(n)
代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 4 const int N=105; 5 vector<int>G[N],level[N]; 6 int max_dep; 7 bool have_son[N]; 8 void dfs(int u,int dep){ 9 level[dep].push_back(u); 10 max_dep=max(max_dep,dep); 11 for(int i=0;i<G[u].size();i++){ 12 dfs(G[u][i],dep+1); 13 } 14 } 15 int main(){ 16 int n,m,id,k,son; 17 scanf("%d%d",&n,&m); 18 for(int i=1;i<=m;i++){ 19 scanf("%d%d",&id,&k); 20 for(int j=1;j<=k;j++){ 21 scanf("%d",&son); 22 if(id<=0||id>=100)continue; 23 else G[id].push_back(son); 24 } 25 if(id<=0||id>=100)continue; 26 else have_son[id]=1; 27 } 28 if(n<=0||n>=100){ 29 printf("0"); 30 return 0; 31 } 32 max_dep=1; 33 dfs(1,1); 34 printf("%d",!have_son[level[1][0]]); 35 for(int i=2;i<=max_dep;i++){ 36 int leaf=0; 37 for(int j=0;j<level[i].size();j++) 38 if(!have_son[level[i][j]]) 39 leaf++; 40 printf(" %d",leaf); 41 } 42 return 0; 43 }
I.Auto Spell Corrector回到顶部
题意
给一张词典表,每次查询给出一个单词
1、如果单词在词典表中,直接输出
2、如果单词可以通过替换一对字母得到字典表中的代词,按字典序输出所有情况
3、如果上述都不满足,直接输出
题解
暴力模拟,复杂度O(40n^3)
代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=105; 4 bool check(string a,string b){ 5 if(a.size()!=b.size())return false; 6 for(int i=0;i<a.size();i++) 7 for(int j=0;j<b.size();j++){ 8 if(i==j)continue; 9 swap(a[i],a[j]); 10 if(a==b)return true; 11 swap(a[j],a[i]); 12 } 13 return false; 14 } 15 int main(){ 16 int t,n,m,ca=0; 17 string s[N],word; 18 cin>>t; 19 while(t--){ 20 if(ca++)cout<<'\n'; 21 cin>>n; 22 for(int i=1;i<=n;i++)cin>>s[i]; 23 sort(s+1,s+1+n); 24 cin>>m; 25 for(int i=1;i<=m;i++){ 26 cin>>word; 27 int out=0; 28 for(int j=1;j<=n;j++) 29 if(word==s[j]){ 30 cout<<word; 31 goto e; 32 } 33 for(int j=1;j<=n;j++){ 34 if(check(word,s[j])){ 35 if(out++)cout<<','; 36 cout<<s[j]; 37 } 38 } 39 if(!out)cout<<word; 40 e:cout<<'\n'; 41 } 42 } 43 return 0; 44 }
J.数据结构练习题――中序遍历二叉树回到顶部
题意
给一颗顺序存储的二叉树,求深度和中序遍历
题解
当前节点i,左儿子i*2,右儿子i*2+1,复杂度O(n)
代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 4 int a[1005],tot,out[1005],cnt,deep; 5 void dfs(int u,int dep){ 6 if(u>tot||a[u]==0)return; 7 deep=max(deep,dep); 8 dfs(u<<1,dep+1); 9 out[cnt++]=a[u]; 10 dfs(u<<1|1,dep+1); 11 } 12 int main(){ 13 int t; 14 scanf("%d",&t); 15 while(t--){ 16 tot=0; 17 while(1){ 18 scanf("%d",&a[++tot]); 19 if(a[tot]==-1)break; 20 } 21 tot--;deep=1;cnt=0; 22 dfs(1,1); 23 printf("%d",deep); 24 for(int i=0;i<cnt;i++)printf(" %d",out[i]); 25 puts(""); 26 } 27 return 0; 28 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号