dp 选练(基础版)
P5664
题目描述:
Emiya 是个擅长做菜的高中生,他共掌握 \(n\) 种烹饪方法,且会使用 \(m\) 种主要食材做菜。为了方便叙述,我们对烹饪方法从 \(1 \sim n\) 编号,对主要食材从 \(1 \sim m\) 编号。
Emiya 做的每道菜都将使用恰好一种烹饪方法与恰好一种主要食材。更具体地,Emiya 会做 \(a_{i,j}\) 道不同的使用烹饪方法 \(i\) 和主要食材 \(j\) 的菜(\(1 \leq i \leq n\)、\(1 \leq j \leq m\)),这也意味着 Emiya 总共会做 \(\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m} a_{i,j}\) 道不同的菜。
Emiya 今天要准备一桌饭招待 Yazid 和 Rin 这对好朋友,然而三个人对菜的搭配有不同的要求,更具体地,对于一种包含 \(k\) 道菜的搭配方案而言:
- Emiya 不会让大家饿肚子,所以将做至少一道菜,即 \(k \geq 1\)
- Rin 希望品尝不同烹饪方法做出的菜,因此她要求每道菜的烹饪方法互不相同
- Yazid 不希望品尝太多同一食材做出的菜,因此他要求每种主要食材至多在一半的菜(即 \(\lfloor \frac{k}{2} \rfloor\) 道菜)中被使用
这里的 \(\lfloor x \rfloor\) 为下取整函数,表示不超过 \(x\) 的最大整数。
这些要求难不倒 Emiya,但他想知道共有多少种不同的符合要求的搭配方案。两种方案不同,当且仅当存在至少一道菜在一种方案中出现,而不在另一种方案中出现。
Emiya 找到了你,请你帮他计算,你只需要告诉他符合所有要求的搭配方案数对质数 \(998,244,353\) 取模的结果。
对于所有测试点,保证 \(1 \leq n \leq 100\),\(1 \leq m \leq 2000\),\(0 \leq a_{i,j} \lt 998,244,353\)。
题目分析:
首先简化题意,对于每一行只能选一个点,对于每一列选的个数不能超过总个数的一半,这种选择方案的贡献就是选的点的 \(a_{i,j}\) 的乘积,求出所有可能方案的贡献和。
每一行就选一个点好处理,但是每一列不能超过选择总数的一半非常难做,一个很显然的思路就是用总的方案减去某一列大于选择总数一半的方案数。
发现大于选择总数一半的列只有一列,所以我们可以直接枚举这一列。
现在有一个 \(dp\),即 \(dp[i][j][k]\) 表示前 \(i\) 行,选了 \(j\) 个数,个数最多的的一列的个数为 \(k\) 的贡献和。
以下数组中,\(s[i][j]\) 表示 \(i\) 这一行不选第 \(j\) 个剩下的 \(a[i]\) 的和。
复杂度为 \(n^3m\)。
考虑怎么优化,肯定需要降维,这里有一个很典的方法,虽然我是第一次学,发现 \(j,k\) 这两维其实可以合并成一维,也就是 \(k-(j-k)\),即个数最多的一列和其他列个数的差。
即设 \(dp[i][j]\) 表示处理的前 \(i\) 行,最大个数列与其他列的个数差为 \(j\) 的贡献和。
最后用总数减去差 \(\ge0\) 的贡献和。
考虑总数怎么计算,每一行任选一个,把他们的权值乘起来:
即 \(\prod_{i=1}^{n}(s[i][m]+1)\),这里的 \(+1\) 是每一行可能有不选的情况,最后总数还要减去 \(1\),因为会有一个都不选的情况出现。
代码:
LL dp[102][300];
int a[102][2007],n,m;
LL s[102][2007],ans=1;
LL M(LL x){return (x%mod+mod)%mod;}
signed main(){
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++){
for (int j=1;j<=m;j++){
scanf("%d",&a[i][j]);
s[i][0]=M(s[i][0]+a[i][j]);
}
}
for (int i=1;i<=n;i++){
for (int j=1;j<=m;j++){
s[i][j]=M(s[i][0]-a[i][j]%mod);
}
}
for (int i=1;i<=n;i++) ans=M(ans*M(s[i][0]+1));
ans=M(ans-1);
for (int k=1;k<=m;k++){ //枚举的某一列
memset(dp,0,sizeof dp);
dp[0][n]=1;
for (int i=1;i<=n;i++){
for (int j=n-i;j<=n+i;j++){
dp[i][j]=M(dp[i-1][j]+M(dp[i-1][j+1]*s[i][k])+M(a[i][k]*dp[i-1][j-1]));
}
}
for (int i=1;i<=n;i++) ans=M(ans-dp[n][n+i]);
}
printf("%lld\n",ans);
return 0;
}
P6748
题目描述:
L 国有 \(n\) 个城市,它们之间有 \(n-1\) 条道路,形成了一棵树的结构。
国王 L 派遣了一些军队来驻守这些道路,驻守每一条道路的军队战斗力都可以被量化为 \([1,m]\) 中的整数。
每个城市都有一个城主,第 \(i\) 个城主有一个忍耐度 \(a_i\)。如果国王 L 在与第 \(i\) 个城市相连的所有道路上驻守的军队战斗力的中位数超过了城主的忍耐度,那么城主就会认为国王不信任他而产生谋反的心理。
国王 L 当然不希望有人造反,但他又想使驻守道路的军队的总战斗力最大来保证国防安全。现在他找到了 L 国最强的 OIer —— 您,去来帮助他解决这个问题。
如果无论如何安排军队都会有人想要造反,那么输出 -1。
注:对于任意 \(k\) 个数,它们的中位数是将这些数从小到大排序后第 \(\left\lfloor\dfrac{k}{2}\right\rfloor+1\) 个数。
对于所有数据,\(1\le u_i,v_i \le n\le 5\times 10^5\),\(n\ge 2\),\(1\le a_i\le m\le 10^9\)。
题目分析:
dp 好题,这种处理儿子和父亲要一起处理的题目非常经典。
首先,没有无解的情况,因为每条边我都选 \(1\),必然可行。
接着边的中位数 \(\le a_i\),相当于有 \(deg_i/2+1\)(\(deg_i\) 是 \(i\) 的度数)条边 \(\le a_i\)。
因为我们最难搞得就是两点之间的边的大小关系。
设 \(f_{i,0/1}\),第一维表示在 \(i\) 点,第二维表示边和点之间的数量关系: $val(u,fa)\le a_u / val(u,fa) > a_u $,存的值为合法的边权和最大值。
设 \(g_{i,0/1}\),第一维表示在 \(i\) 点,第二维表示边和点之间的数量关系:\(val(u,fa)\le a_{fa_u}/val(u,fa)>a_{fa_{u}}\),存的值为合法的边权和最大值。
答案就是 \(f_{1,0}\)。
考虑如何转移:
\(f_{u,0}\) 可以选 \(deg_u-(deg_u/2+1)\) 条 \(>a_u\) 的边,\(f_{u,1}\) 可以选 \(deg_u-(deg_u/2+1)-1\) 条 \(>a_u\) 的边,因为 \(val(u,fa)>a_u\) 已经占掉了一条边,把能选的边数设为 \(k\)。
所以先把 \(g_{v,0}\) 全部加入到 \(f_{u,0}\) 和 \(f_{u,1}\) 中,然后把 \(g_{u,1}-g_{u,0}\) 加入到数组中,从大到小排序,选出前 \(k\) 大,加入到 \(f_{u,0/1}\) 中,注意如果选到 \(g_{u,1}-g_{u,0}<0\) 的,那就停止,否则选满 \(k\) 个。
接着考虑 \(g\) 数组。下面的 \(dp\) 转移,可以先看一个,然后顺着上面设的 \(dp\) 状态举一反三。
如果 \(a_u\le a_{fa_u}\):
- \(g_{u,0}\) :
- \(a_u<val\le a_{fa_u}\) (\(f_{u,1}+a_{fa_u}\))
- \(val<a_u\le a_{fa_u}\) (\(f_{u,0}+a_u\))
- \(g_{u,1}\):
- \(a_u\le a_{fa_u}<val\le m\) (\(f_{u,1}+m\))
否则:
- \(g_{u,0}\):
- \(val\le a_{fa_u}<a_u\) (\(f_{u,0}+a_{fa_u}\))
- \(g_{u,1}\):
- \(a_{fa_u}<a_u<val\le m\) (\(f_{u,1}+m\))
- \(a_{fa_u}<val\le a_u\) (\(f_{u,0}+a_u\))
注意如果 \(deg_i\le2\),那么 \(val(u,fa)\) 一定 \(\le a_u\),把 \(f_{u,1}\) 设为最小值即可。
代码:
int n,a[N],m,deg[N];
int tmp[N];
int f[N][2],g[N][2];
vector<int> G[N];
bool cmp(int a,int b){
return a>b;
}
void dfs(int u,int fa){
int cnt=0;
int x=deg[u]-deg[u]/2-1,y=deg[u]-deg[u]/2-2;
for (auto v:G[u]) if (v!=fa) dfs(v,u); // 注意,要先全部递归完,在进行选择的操作,不然会有数值还未转移就被传上来转移了
for (auto v:G[u]){
if (v==fa) continue;
f[u][1]+=g[v][0];
tmp[++cnt]=g[v][1]-g[v][0];
}
sort(tmp+1,tmp+cnt+1,cmp);
for (int i=1;i<=y&&tmp[i]>0;i++)
f[u][1]+=tmp[i];
f[u][0]=f[u][1];
if (tmp[x]>0) f[u][0]+=tmp[x];
if (deg[u]<=2) f[u][1]=-INF;
if (a[u]<=a[fa]){
g[u][0]=max(f[u][1]+a[fa],f[u][0]+a[u]);
g[u][1]=f[u][1]+m;
}
else{
g[u][0]=f[u][0]+a[fa];
g[u][1]=max(f[u][1]+m,f[u][0]+a[u]);
}
}
signed main(){
scanf("%lld%lld",&n,&m);
for (int i=1;i<=n;i++) scanf("%lld",&a[i]);
for (int i=1;i<n;i++){
int u=read(),v=read();
G[u].p_b(v);G[v].p_b(u);
deg[u]++;deg[v]++;
}
dfs(1,0);
printf("%lld",f[1][0]);
return 0;
}
P1073
题目描述:
\(C\) 国有 \(n\) 个大城市和 \(m\) 条道路,每条道路连接这 \(n\) 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 \(m\) 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的道路在统计条数时也计为 \(1\) 条。
\(C\) 国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价格不一定相同。但是,同一种商品在同一个城市的买入价和卖出价始终是相同的。
商人阿龙来到 \(C\) 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后,便决定在旅游的同时,利用商品在不同城市中的差价赚回一点旅费。设 \(C\) 国 \(n\) 个城市的标号从 \(1\sim n\),阿龙决定从 \(1\) 号城市出发,并最终在 \(n\) 号城市结束自己的旅行。在旅游的过程中,任何城市可以重复经过多次,但不要求经过所有 \(n\) 个城市。阿龙通过这样的贸易方式赚取旅费:他会选择一个经过的城市买入他最喜欢的商品――水晶球,并在之后经过的另一个城市卖出这个水晶球,用赚取的差价当做旅费。由于阿龙主要是来 \(C\) 国旅游,他决定这个贸易只进行最多一次,当然,在赚不到差价的情况下他就无需进行贸易。
假设 \(C\) 国有 \(5\) 个大城市,城市的编号和道路连接情况如下图,单向箭头表示这条道路为单向通行,双向箭头表示这条道路为双向通行。
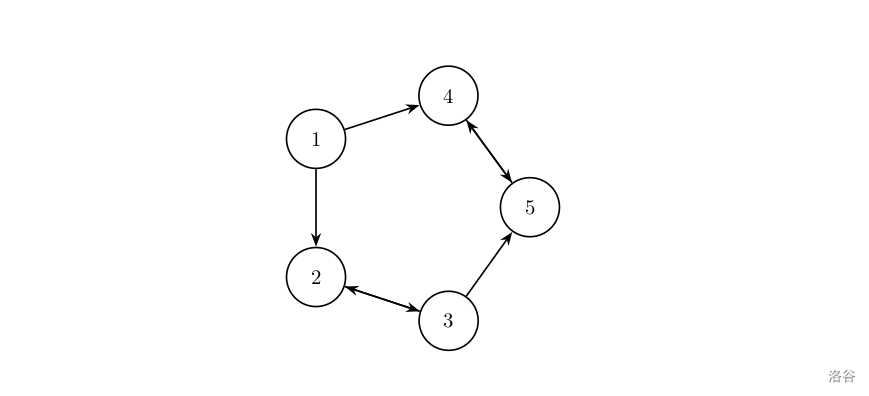
假设 \(1\sim n\) 号城市的水晶球价格分别为 \(4,3,5,6,1\)。
阿龙可以选择如下一条线路:\(1\to2\to3\to5\),并在 \(2\) 号城市以 \(3\) 的价格买入水晶球,在 \(3\) 号城市以 \(5\) 的价格卖出水晶球,赚取的旅费数为 \(2\)。
阿龙也可以选择如下一条线路:\(1\to4\to5\to4\to5\),并在第 \(1\) 次到达 \(5\) 号城市时以 \(1\) 的价格买入水晶球,在第 \(2\) 次到达 \(4\) 号城市时以 \(6\) 的价格卖出水晶球,赚取的旅费数为 \(5\)。
现在给出 \(n\) 个城市的水晶球价格,\(m\) 条道路的信息(每条道路所连接的两个城市的编号以及该条道路的通行情况)。请你告诉阿龙,他最多能赚取多少旅费。
对于 \(100\%\) 的数据,\(1\leq n\leq 100000\),\(1\leq m\leq 500000\),\(1\leq x,y\leq n\),\(1\leq z\leq 2\),$1\leq $ 各城市的编号 \(\leq n\),水晶球价格 \(\leq 100\)。
题目分析:
先考虑没有反向变怎么做,可以设 \(dp_i\) 表示走到 \(i\) 时经过的点的最小值是多少,\(g_i\) 表示走到 \(i\) 时已经卖过的最大值,答案就是 \(g_n\)。
有反向边的话可以直接用 tarjan 把他转化成没有反向边,对于一个强联通分量,我可以以其中的最小值买来,最大值卖掉,所以记录一下最小值和最大值即可,\(dp\) 同上。
代码:
int m,n,a[N],ans=0,f[N],deg[N],g[N];
int dfn[N],low[N],cnt,tot,stk[N],top,id[N];
PII b[N];
bool vis[N];
vector<int> G1[N],G2[N];
void tarjan(int u){
dfn[u]=low[u]=++cnt;
stk[++top]=u;vis[u]=1;
for (auto v:G1[u]){
if (!dfn[v])
tarjan(v),low[u]=min(low[u],low[v]);
else if (vis[v]) low[u]=min(low[u],dfn[v]);
}
if (low[u]==dfn[u]){
int y;tot++;
b[tot].se=INF;
do{
y=stk[top--],b[tot].fi=max(b[tot].fi,a[y]);
b[tot].se=min(b[tot].se,a[y]);id[y]=tot;vis[y]=0;
}while(y!=u);
}
}
void topo(){
queue<int> q;
for (int i=1;i<=tot;i++) if (!deg[i]) q.push(i);
while(!q.empty()){
int u=q.front();q.pop();
f[u]=min(f[u],b[u].se);
for (auto v:G2[u]){
f[v]=min(f[v],f[u]);
deg[v]--;if (!deg[v]) q.push(v);
}
g[u]=max(g[u],b[u].fi-f[u]);
for (auto v:G2[u])
g[v]=max(g[v],g[u]);
}
}
signed main(){
memset(f,0x3f,sizeof f);
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++) scanf("%d",&a[i]);
for (int i=1;i<=m;i++){
int u=read(),v=read(),op=read();
G1[u].p_b(v);
if (op==2) G1[v].p_b(u);
}
tarjan(1);
for (int u=1;u<=n;u++){
for (auto v:G1[u]){
if (id[v]!=id[u]) G2[id[u]].p_b(id[v]),deg[id[v]]++;
}
}
topo();
printf("%d",g[id[n]]);
return 0;
}


