数论
数论(不定时更新)
卡特兰数:
给定 \(n\) 个 \(0\) 和 \(n\) 个 \(1\) ,它们将按照某种顺序排成长度为 \(2n\) 的序列,求它们能排列成的所有序列中,能够满足任意前缀序列中 \(0\) 的个数都不少于 \(1\) 的个数的序列有多少个。
我们可以把他转化成图上问题,如下,假设 \(0\) 是向右走,\(1\) 是向上走,那么对应到题目里就是无论什么时刻,我们在的点都要 \(x > y\) 所以无论什么时候最多只能走到蓝线上,然后我们在进一步,在任意时刻都不能走到红线上,这样就能用容斥的思想了。
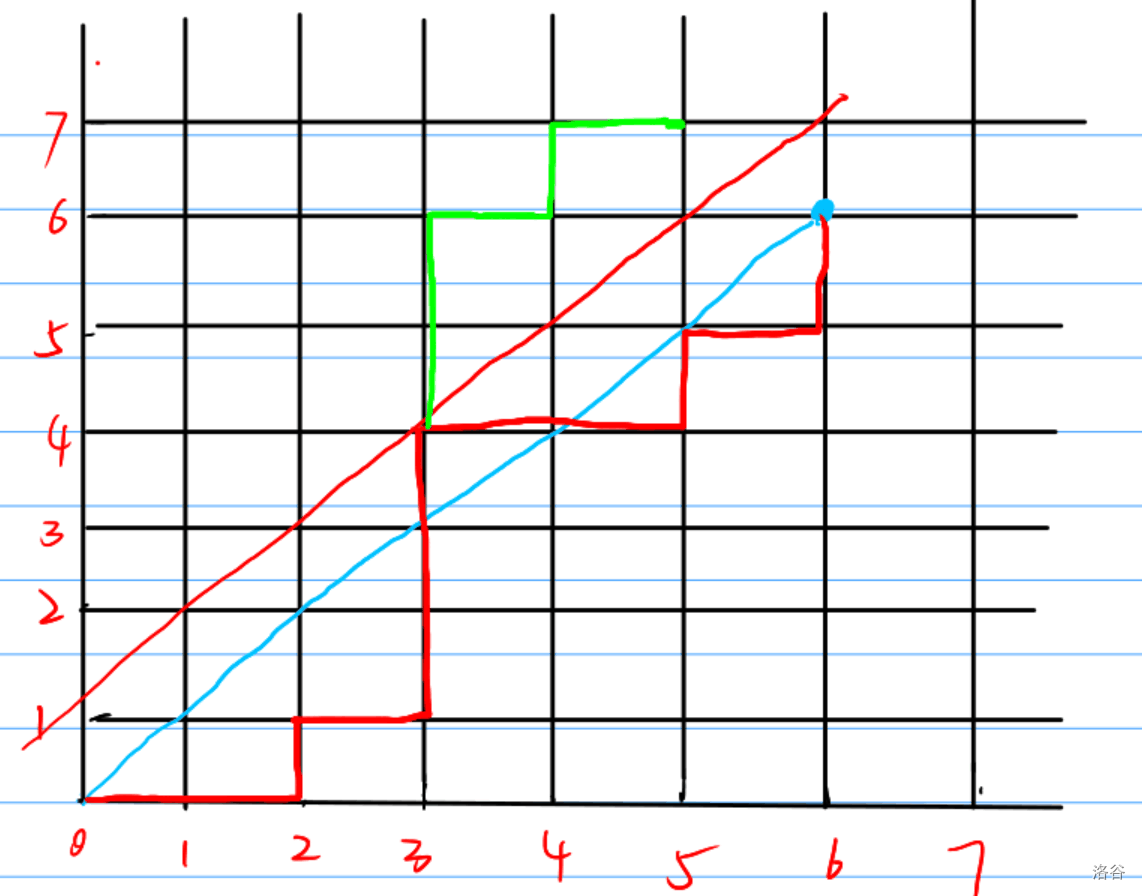
那么从 \(1\) 走到蓝点 \((6,6)\) 的方案数就是:\(C_{12}^6\) 。
接下来就是走过红线的方案数:

我们可以把任意一条走过红线的路径(红色路径),我们从走到红线的点开始沿着红线折叠,所以每条走过红线的点都可以转化成走到 \((5,7)\) 这个点。
所以走到 \((5,7)\) 这个点的方案数就是走过红线到蓝点的方案数:\(C_{12}^5\) 。
所以走下面的方案数就是:
\(C_{12}^6-C_{12}^5\)
所以求卡特兰数就是:
\(C_{2n}^n-C_{2n}^{n-1}\)
进一步:
怎么转化成 \(\frac{C_{2n}^n}{(n+1)}\)
\(C_{2n}^n-C_{2n}^{n-1}=\frac{(2n)!}{(n!\times n!)}-\frac{(2n)!}{(n-1)!\times(n+1)!}=\frac{(2n)!}{(n!\times n!)}-\frac{(2n)!}{n! \times (\frac{1}{n})\times n!\times (n+1)}\)
\(=C_{2n}^{n} \times (1-\frac{1}{\frac{1}{n}\times (n+1)})=C_{2n}^{n} \times (1-\frac{n}{n+1})=C_{2n}^n \times (\frac{1}{n+1})\)
这样就转化完了
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=1e9+7;
int n,a,b;
int qmi(int a,int k)
{
int res=1;
while(k)
{
if (k&1) res=(res*a)%mod;
a=(a*a)%mod;
k>>=1;
}
return res;
}
int C(int a,int b)
{
int res=1;
for (int i=a;i>b;i--) res=res*i%mod;
for (int i=1;i<=b;i++) res=res*qmi(i,mod-2)%mod;
return res;
}
signed main()
{
cin>>n;
cout<<(C(2*n,n)%mod*qmi(n+1,mod-2)%mod+mod)%mod<<endl;
return 0;
}
欧拉函数:
先对于 \(i\) 质因数分解
\(i=p_1^{k_1}+p_2^{k_2}+....+p_k^{k_k}\)
则对于 \(i\) 的欧拉函数
\(\varphi_i=i\times(1-\frac{1}{p_1})\times(1-\frac{1}{p_2})\times...\times(1-\frac{1}{p_k})\)
其实非常好理解对吧,就是一个容斥原理
把从 \(1\) 到 \(i\) 中 去掉 \(p_1,p_2,...p_k\) 的所有倍数
在把被重复减去的数加回来(一个数会被减l两次)
然后有的数会被 \(p_1p_2p_3\) 同时加上,那又要减去
\(i-\frac{i}{p_1}-\frac{i}{p_2}-...-\frac{i}{p_k}\)
\(+\frac{i}{p_1p_2}+\frac{1}{p_2p_3}...\)
\(-\frac{1}{p_1p_2p_3}-...\)
把上面的式子给乘开其实就是这样的
然后就是怎么线性筛求欧拉函数:
首先给个线性筛质数时的代码(筛欧拉函数就是加了点东西):
const int N=2e6+7;
#define int long long
int n,cnt,prime[N],ans=0;
bool check[N];
void init(int n)
{
phi[1]=1;
for (int i=2;i<=n;i++)
{
if (!check[i])
prime[++cnt]=i;
for (int j=1;prime[j]*i<=n;j++)
{
check[prime[j]*i]=1;
if (i%prime[j]==0)
break;
}
}
}
\(\varphi_1=1\)
第一个如果 \(i\) 是一个质数,那么 \(\varphi_i=i-1\)
如果 \(i\%prime[j]=0\)
那就说明 \(prime[j]\) 是 \(i\) 的一个因数
\(\varphi_i=i\times(1-\frac{1}{p_1})\times(1-\frac{1}{p_2})\times...\times(1-\frac{1}{p_k})\)
然后因为 \(\varphi_i\) 里面肯定也有这些质因数,而且因为 \(prime[j]\) 是 \(i\) 的一个因数
所以 \(\varphi[i\times prime[j]]=prime[j]\times i\times(1-\frac{1}{p_1})\times(1-\frac{1}{p_2})\times...\times(1-\frac{1}{p_k})\)
\(=prime[j]\times \varphi[i]\)
如果 \(i\%prime[j]!=0\)
\(\varphi[i\times prime[j]]=prime[j]\times (1-\frac{1}{prime[j]})\times i \times(1-\frac{1}{p_1})\times(1-\frac{1}{p_2})\times...\times(1-\frac{1}{p_k})\)
\(=(prime[j]-1)\times phi[i]\)
代码:
const int N=2e6+7;
#define int long long
int n,cnt,phi[N],prime[N],ans=0;
bool check[N];
void init(int n)
{
phi[1]=1;
for (int i=2;i<=n;i++)
{
if (!check[i])
{
prime[++cnt]=i;
phi[i]=i-1;
}
for (int j=1;prime[j]*i<=n;j++)
{
check[prime[j]*i]=1;
if (i%prime[j]==0)
{
phi[i*prime[j]]=prime[j]*phi[i];
break;
}
phi[i*prime[j]]=phi[i]*(prime[j]-1);
}
}
}
快速幂求逆元(在 \(mod\) 是质数时 :
\(b^{mod-1}\equiv1(\%mod)\)
则 \(b\times b^{mod-2}\equiv1(\%mod)\)
也就是 \(b^{mod-2}\%p\)
所以直接求就可以了
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int b,mod;
int qmi(int a,int k)
{
int res=1;
while(k)
{
if (k&1) res=(res*a)%mod;
a=(a*a)%mod;
k>>=1;
}
return res;
}
signed main()
{
int T;
cin>>T;
while(T--)
{
cin>>b>>mod;
if (b%mod==0)
{
cout<<"impossible"<<endl;
continue;
}
cout<<qmi(b,mod-2)<<endl;
}
return 0;
}
扩展欧几里得算法:
其实就是在欧几里得算法进一步
\(ax+by=gcd(a,b)\)
设 \(d=gcd(a,b)\)
我们写欧几里得的时候:
int gcd(int a,int b)
{
if (b==0)
{
return a;
}
int d=gcd(b,a%b);
return d;
}
其实就是这样的,然后我们在其中加上 \(x,y\)
当 \(b=0\) 时,\(x=1,y=0\)
当第二次传参数的时候:
\(by+(a\%b)x=d\)
\(by+(a - \lfloor \frac{a}{b}\rfloor \times b)x=d\)
\(ax+b(y-x \lfloor \frac{a}{b}\rfloor)=d\)
这个时候 \(y \to y-x\times\lfloor\frac{a}{b}\rfloor\) , \(x\) 不变
代码:
int exgcd(int a,int b,int x,int y)
{
if (b==0)
{
x=1,y=0;
return a;
}
int d=gcd(b,a%b,y,x);
y=y-a/b*x;
return d;
}
一道题目的小应用

这道题就只能用 \(exgcd\) 因为 \(m_i\) 不一定是质数
#include<bits/stdc++.h>
using namespace std;
#define int long long
int exgcd(int a,int b,int &x,int &y)
{
if (b==0)
{
x=1,y=0;
return a;
}
int d=exgcd(b,a%b,y,x);
y-=a/b*x;
return d;
}
signed main()
{
int T;
cin>>T;
while(T--)
{
int a,b,m;
cin>>a>>b>>m;
int x,y;
int d=exgcd(a,m,x,y);
if (b%d!=0)
cout<<"impossible"<<endl;
else
cout<<x*(b/d)%m<<endl;
}
return 0;
}
中国剩余定理:
\(m_1,m_2,...,m_k\) 两两互质
求解 \(x\)
中国剩余定理其实是一个构造的过程:
首先:
\(M=m_1 \times m_2 \times ... \times m_n\)
\(M_i=\frac{M}{m_i}\)
\(M_i^{-1}\) 是 \(M_i\) 关于 \(m_i\) 的逆元,即:\(M_i\times M_i^{-1} \equiv 1 ( \mod m_i)\)
则
然后我们可以验证一下这个对不对
首先,对于 \(\mod m_1\) 则答案会变成 \(a_1\times 1 +a_2\times 0+...+a_n \times 0\)
解释一下为什么后面都是 \(\times 0\) 因为除了 \(M_1\) 外 每一个 \(M_i\) 都是 \(m_1\) 的倍数,所以一取模就变成 \(0\) 了,而 \(M_1\times M_1^{-1} \% m_i =1\) ,所以这个地方是 \(1\)
则此时的答案就是 \(a_1\) 以此类推
因为 \(m_i\) 不一定是个质数,所以求的时候要用到 \(exgcd\)
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+7;
int M=1,a[N],m[N],n,res;
int exgcd(int a,int b,int &x,int &y)
{
if (b==0)
{
x=1,y=0;
return a;
}
int d=exgcd(b,a%b,y,x);
y-=a/b*x;
return d;
}
signed main()
{
cin>>n;
for (int i=1;i<=n;i++)
{
cin>>a[i]>>m[i];
M*=a[i];
}
for (int i=1;i<=n;i++)
{
int Mi=M/a[i];
int ti,x;
exgcd(Mi,a[i],ti,x);
res+=m[i]*Mi*ti;
}
cout<<(res%M+M)%M;
return 0;
}
高斯消元
其实高斯消元没什么好说的,就是非常简答的解方程组
- 找当前列最大(找主元即当前列绝对值最大的那个)
- 交换(把主元所在的这一列放在最上方)
- 归一(把这个主元变成 \(1\) )
- 把这一列除了这个数之外的所有数通过方程的加减来变成 \(0\)
这样的话每一列只会有一个数不为 \(0\)
这个时候把每一列剩下的数变成 \(1\) 这样就解出了答案
代码:
void Gauss() {
//化成上三角矩阵
for (int r = 1, c = 1; r <= n; ++ r, ++ c) {
//找到主元,r是行,c是列
int t = r;
for (int i = r + 1; i <= n; ++ i)
if (fabs(b[i][c]) > fabs(b[t][c]))
t = i;
//交换第r行和第t行的元素
for (int i = c; i <= n + 1; ++ i) swap(b[r][i], b[t][i]);
//主元归一(第r行除以主元系数)
for (int i = n + 1; i >= c; -- i) b[r][i] /= b[r][c];
//消元(用该行把下面所有行的第c列消为0)
for (int i = r + 1; i <= n; ++ i) { //当前列下面的每一行
for (int j = n + 1; j >= c; -- j) { //在当前行第 c 列之后的每个数都会变
b[i][j] -= b[r][j] * b[i][c];
}
}
}
//化成行最简阶梯型矩阵(本题唯一解,故同样也是对角矩阵)
for (int i = n; i > 1; -- i) {
for (int j = i - 1; j >= 1; -- j) {
b[j][n + 1] -= b[i][n + 1] * b[j][i];
b[j][i] = 0;
}
}
}

