网络流
不定时更新......
1.网络流的基本概念
1.1 流网络(不考虑反向边)
什么是流网络?画个图就明白了
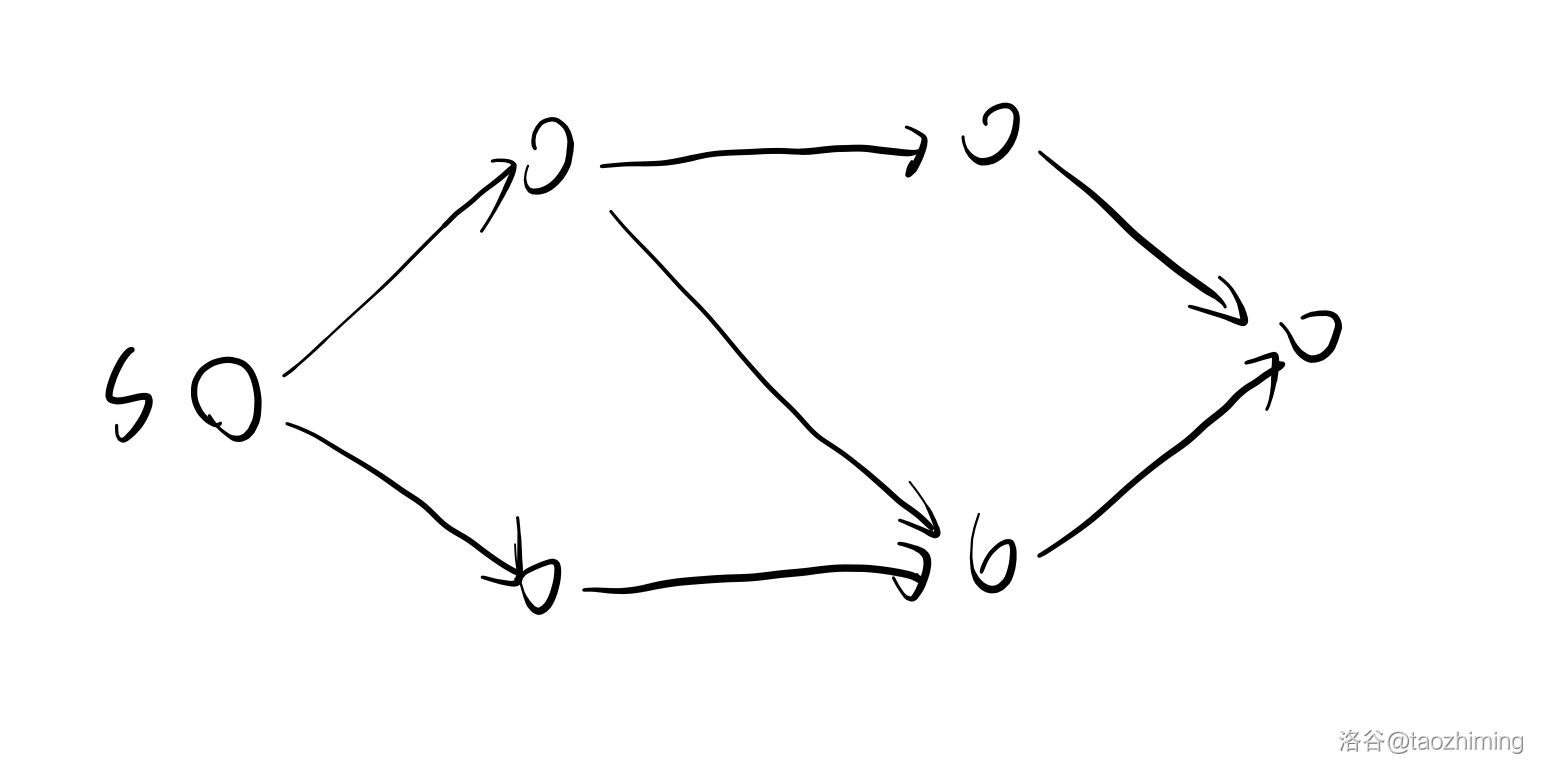
1.2 可行流(不考虑反向边)

\(/\) 左边的是流量 \(/\) 右边的是可行流的容量
我们定义每条边的容量为 \(c(u,v)\)
每条边的流量为 \(f(u,v)\)
1.2.1 两个条件:容量限制,流量守恒
容量限制的意思就是对于每条边的流量都要小于容量
流量守恒就是除了原点和汇点之外的所有点都需要保证流入的流量等于流出的流量
1.2.2 可行流的流量是指从原点流出的流量 - 流入原点的流量
1.2.3 最大流是指最大可行流
1.3 残留网络(考虑反向边)
1.3.1 什么是残留网络?
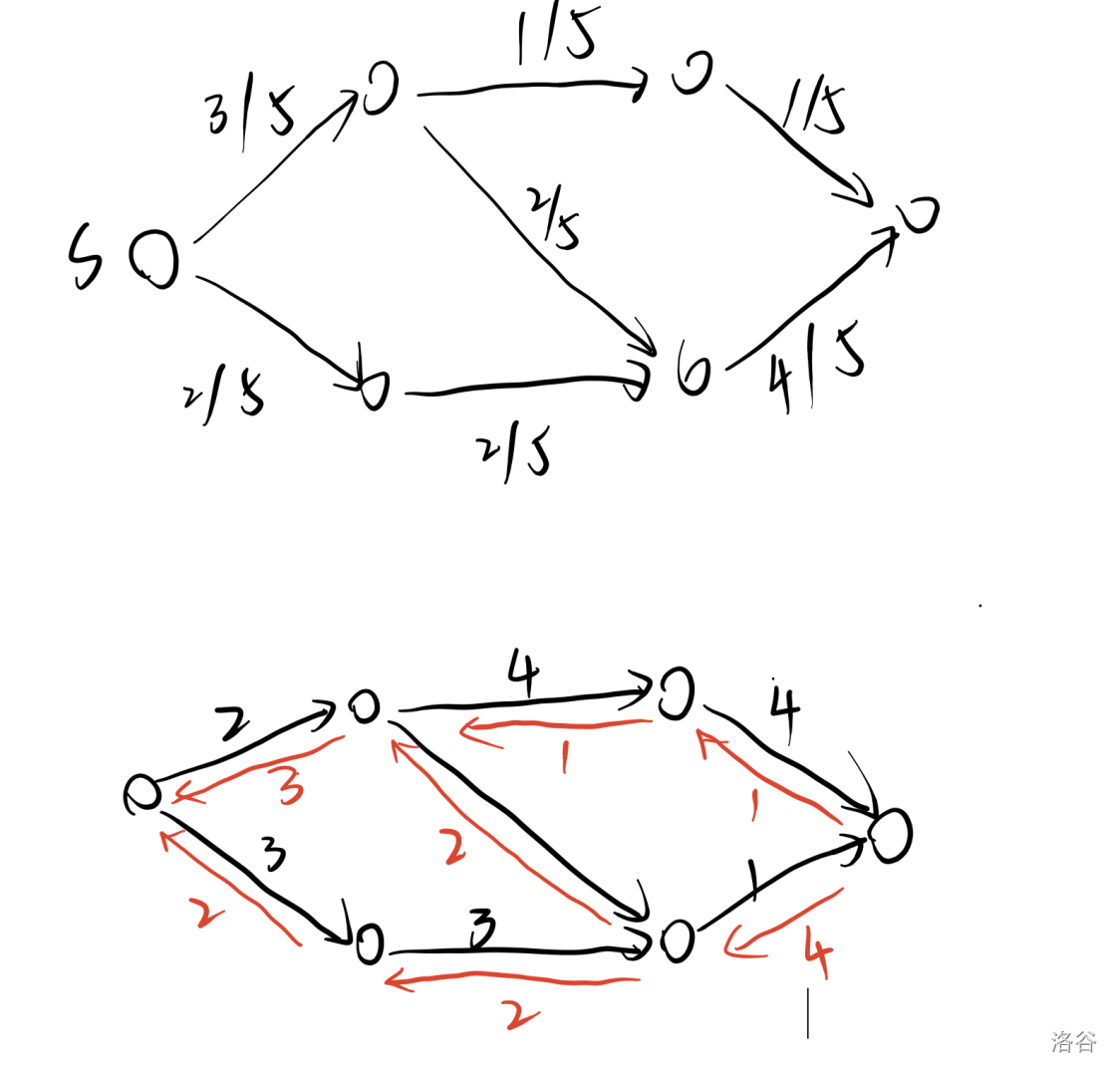
残留网络是怎么构造的?
-
和原图方向相同的边 残留网络的容量 \(c'(u,v)\)=\(c(u,v)-f(u,v)\)
-
在任何时候,一个网络流的反向边的容量都是正向边的流量
和原图方向相反的边 残留网络的容量 \(c'(u,v) = f(v,u)\) 意义就是想要返悔,所以想要退流就不能超过原先流过的流量
1.3.2 定理:残留网络中的可行流 \(f'\) + 原图中的可行流 \(f\) = 原体中的另外一个可行流
两个流量是怎么相加的呢?
如果说两条边的方向相同,则把对应边的流量加起来就可以了
用数学语言就是 \(|f+f'|=|f|+|f'|\)
如果两条边的方向相反,相减就 OK
证明:需要保证两个条件:1.容量限制 2. 流量守恒
- 如果两条边的方向相同
容量限制:
\(f'(u,v)<= c'(u,v)=c(u,v)-f(u,v)\)
也就是说 \(f'(u,v)+f(u,v)<=c(u,v)\)
流量守恒:
因为两条边的流量分别守恒,所以加起来也一定守恒
- 如果两条边的方向相反
容量限制:
\(0<=f'(u,v)<=[c'(u,v)=f(v,u)]<=[c(v,u)=f(u,v)]<=c(u,v)\)
\(0<=f(u,v)-f'(u,v)<=c(u,v)\)
流量守恒是一样的
1.4 增广路径
还是刚刚的图,先画出他的残留网络,发现还有一条路径可以走,这条路径就被叫做增广路径
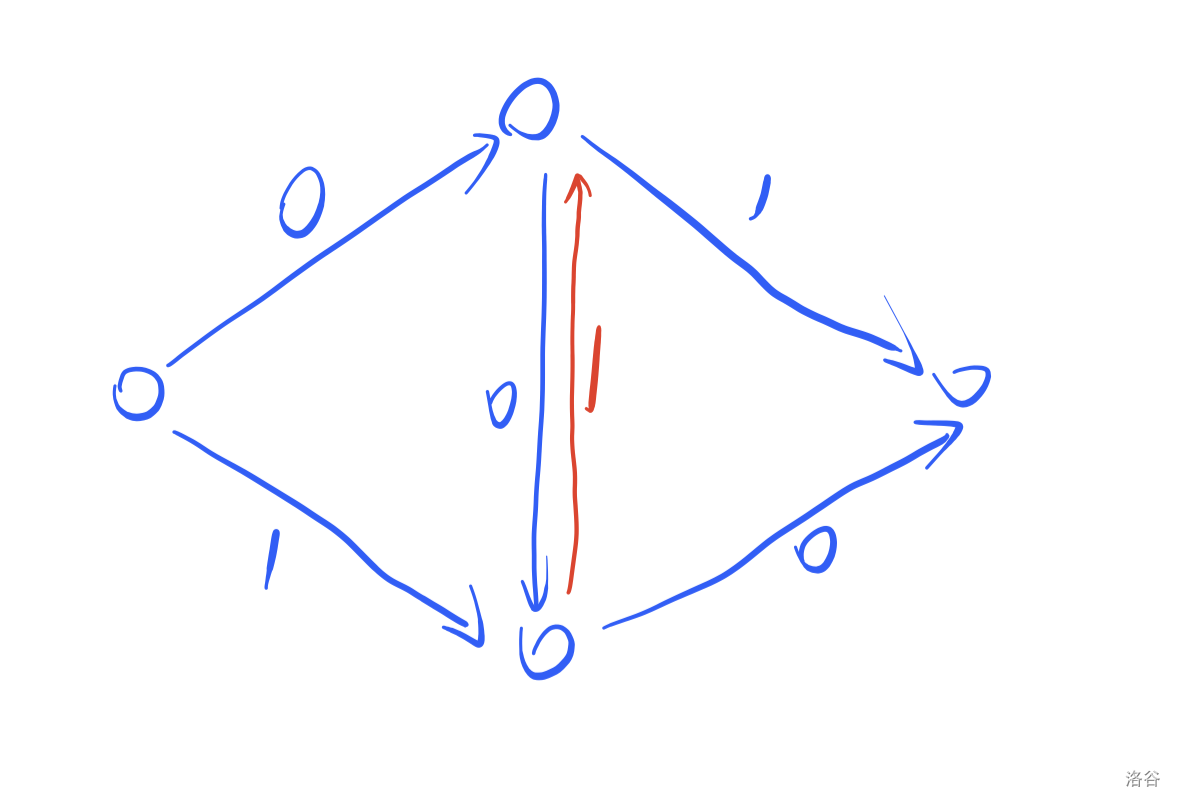
现在引入一个新的定理:对于任意一个流网络,如果这个流没有增广路径了,我们就断言这个流就是本网络的最大流
怎么证明呢?(这个证明说实话没啥用,什么时候闲了再补)
我们要引入一个新的概念(来帮助证明):割
1.5 割
1.5.1 割的定义
割可以把整个点集分成不重不漏的两个点集 \(S\) 和 \(T\)
而且要保证 \(s\in S,t\in T\)
1.5.2 割的容量

割的容量指的是所有从 \(S\) 指向 \(T\) 的边的容量之和
即
最小割是指所有割中容量最小的割
这里我们区分一下,最大流是指最大可行流,是流量,而最小割是容量
1.5.3 割的流量
定义十分简单
即
同时 \(f(S,T)<=c(S,T)\)
1.5.4 对于任意的可行流,任意的割 \((S,T)\) , \(|f|=f(S,T)\)
我们可以直观上理解,当前的流量,想要从 \(S\) 流到 \(T\) 一定会经过当前的割,所以流量就是割的流量
1.5.5 对于任意的可行流,任意的割 \((S,T)\) ,\(|f|<=c(S,T)\)
这个也比较好证明 因为 \(|f|=f(S,T)<=c(S,T)\)
所以 \(|f|<=c(S,T)\)
也就是说 最大流 \(<=\) 最小割
现在分析一些性质
可以得到一下性质
-
\(f(X,Y)=-f(Y,X)\)
-
\(f(X,X)=0\)
-
\(f(X,Y\bigcup Z)=f(X,Y)+f(X,Z)\) 前提:\(Y⋂Z=\empty\)
-
\(f(X\bigcup Y,Z)=f(X,Z)+f(Y,Z)\) 前提:\(X⋂Y=\empty\)
现在我们可以用数学语言证明一下 \(1.5.4\) 了
因为 \(S\bigcup T=V,S\bigcap T=\empty\)
所以
我们设 \(S'=S-\{s\}\)
则
最大流最小割定理
即最大流等于最小割
证明不想写了,想知道的话就去 acwing进阶课 的第一节课去听吧 (反正我感觉证明没啥用)
2.最大流
2.1 EK 算法
这个我不想讲,为啥要提他呢?因为费用流用的是这个模版,如果想知道直接去费用流看
看完下面的 dinic 算法和费用流后,我们比较一下两个算法的不同之处
EK 算法其实是一条增广路径一条增广路径的找,然后更新
dinic 算法是直接搜多条增广路径,一起更新
2.2 dinic 算法
这个还是需要讲一下的,我见过的所有最大流的题目都可以用这个模版
核心思想:
- 看看能不能找到增广路径
- 把可以增广的路径的流量和反向边的流量更新一下,然后当前流量加上增广的流量
代码:
#include <map>
#include <set>
#include <queue>
#include <cmath>
#include <ctime>
#include <stack>
#include <random>
#include <vector>
#include <cstdio>
#include <iomanip>
#include <cstring>
#include <iostream>
#include <algorithm>
#define fi first
#define se second
#define m_p make_pair
#define int long long
#define p_b push_back
#define lowbit(x) x&(-x)
#define PII pair<int,int>
using namespace std;
inline int read(){
int x=0,w=1;
char ch=getchar();
for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*w;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
const int N=2e5+7;
const int INF=1e18+7;
int n,m,S,T,f[N],d[N],cur[N];
int cnt=1,head[N],q[N];
// 需要注意这里的 cnt 要从 2 开始
// 因为我们要建反向边,然后发现 ^ 非常的好用
// 举个例子 1^1=2,2^1=1
// 3^1=4,4^1=3
// 也就是说 只要 ^ 一下就可以找到反向边了
// 其实这里从 0 开始 从 2 开始都可以,只不过从 0 开始的话要主要 head 要设成 -1
// 这里为啥要设成 -1 我也搞不明白
struct node{
int v,nxt;
}e[N];
void add(int u,int v,int w)
{
e[++cnt].v=v;e[cnt].nxt=head[u];head[u]=cnt;f[cnt]=w;
e[++cnt].v=u;e[cnt].nxt=head[v];head[v]=cnt;f[cnt]=0;
}
bool bfs()
{
memset(d,-1,sizeof(d));
int hh=0,tt=0;
q[0]=S,d[S]=0,cur[S]=head[S];
while(hh<=tt)
{
int u=q[hh++];
for (int i=head[u];i;i=e[i].nxt)
{
int v=e[i].v;
if (d[v]==-1&&f[i]) // 如果 f[i] 都空了也就没必要增广这条路了
{
d[v]=d[u]+1;
cur[v]=head[v];
if (v==T) return 1;
q[++tt]=v;
}
}
}
return 0;
}
int find(int u,int limit)
{
if (u==T) return limit;
int flow=0;
for (int i=cur[u];i&&flow<limit;i=e[i].nxt) // 这里 flow < limit 也是必要的剪枝
{
cur[u]=i; // cur 数组其实就是记录之前增广过的路径就不用在继续增广了
// 也算是一个小小的优化
int v=e[i].v;
if (d[v]==d[u]+1&&f[i])
{
int t=find(v,min(limit-flow,f[i]));
if (!t) d[v]=-1;
f[i]-=t,f[i^1]+=t,flow+=t;
}
}
return flow;
}
int dinic()
{
int ans=0;
while(bfs()) ans+=find(S,INF);
return ans;
}
signed main(){
cin>>n>>m>>S>>T;
for (int i=1;i<=m;i++)
{
int u=read(),v=read(),w=read();
add(u,v,w);
}
cout<<dinic();
return 0;
}
3. 费用流
3.1 定义
\(总费用=\sum (每条边的费用 \times 这条边的流量)\)
3.2这里只能提供一种求费用流的方法(因为别的我也没学)
EK 算法
核心思想:
- 找到一条增广路径,把路径记录下来
- 更新流量
需要注意的一些地方:
原先的 EK 算法找增广路径是用的是 bfs
但是现在我们有多个最大流的路径,也就是说费用有最大的,也有最小的
所有就有了两个区分:
- 最大费用最大流
- 最小费用最大流
我们以最大费用为例
这里使用的是 spfa 来求
我们可以把费用当成路径的长度
也就是说最大费用就是求的最长路
而最小费用同理
代码:
#include <map>
#include <set>
#include <queue>
#include <cmath>
#include <ctime>
#include <stack>
#include <random>
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <iomanip>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_set>
#include <unordered_map>
#define fi first
#define se second
#define m_p make_pair
#define int long long
#define p_b push_back
#define lowbit(x) x&(-x)
#define PII pair<int,int>
#define all(x) x.begin(),x.end()
using namespace std;
inline int read(){
int x=0,w=1;
char ch=getchar();
for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*w;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
const int N=5000+7;
const int M=50000*2;
const int INF=1e18+7;
int n,m,S,T;
int cnt=1,head[N];
int pre[N],dis[N],incf[N];
int f[M],flow,cost;
bool vis[N];
struct node{
int v,w,nxt;
}e[M];
void add(int u,int v,int c,int d)
{
e[++cnt].v=v;e[cnt].w=d;f[cnt]=c;e[cnt].nxt=head[u];head[u]=cnt;
e[++cnt].v=u;e[cnt].w=-d;f[cnt]=0;e[cnt].nxt=head[v];head[v]=cnt;
}
bool spfa()
{
queue<int> q;
memset(dis,0x3f,sizeof dis);
memset(incf,0,sizeof incf);
q.push(S);incf[S]=INF;dis[S]=0;
while(!q.empty())
{
int u=q.front();q.pop();
vis[u]=0;
for (int i=head[u];i;i=e[i].nxt)
{
int v=e[i].v;
if (f[i]&&dis[v]>dis[u]+e[i].w)
{
dis[v]=dis[u]+e[i].w;
pre[v]=i;
incf[v]=min(incf[u],f[i]);
if (!vis[v])
{
q.push(v);
vis[v]=1;
}
}
}
}
return incf[T]>0;
}
void EK()
{
flow=cost=0;
while(spfa())
{
int t=incf[T];
flow+=t;cost+=t*dis[T];
for (int i=T;i!=S;i=e[pre[i]^1].v)
{
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
}
signed main(){
cin>>n>>m>>S>>T;
for (int i=1;i<=m;i++)
{
int u=read(),v=read(),c=read(),w=read();
add(u,v,c,w);
}
EK();
cout<<flow<<" "<<cost<<endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号