排序算法学习小结

参考维基百科

0. 一些基本概念
--（体会）空间换时间是进一步提高算法速度的最终方法，比如希尔排序和基数排序就是通过占用额外空间来获得比快速排序更快的速度。当然，空间换不换的到时间，也是要看你写的算法的水平的。
--best, worst and average cases. In computer science, best, worst and average cases of a given algorithm express what the resource usage is at least, at most and on average, respectively. Usually the resource being considered is running time, but it could also be memory or other resources.
   1. example for best case: when doing a search, the first element is the one you look for.
   2. example for worst case: when doing a search, visiting every element to either find it in last position or not find it at all
   3. some algorithms like hash tables have very poor worst case behaviours, but a well written hash table of sufficient size will statistically never give the worst case
--Big O notation： In computer science, it is useful in the analysis of algorithms. If a function f(n) can be written as a finite sum of other functions, then the fastest growing one determines the order of f(n). For example

Notation	Name	Example
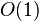	constant	Determining if a number is even or odd; using a constant-size lookup table or hash table
	logarithmic	Finding an item in a sorted array with a binary search or a balanced search tree as well as all operations in a Binomial heap.
	fractional power	Searching in a kd-tree
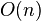	linear	Finding an item in an unsorted list or a malformed tree (worst case) or in an unsorted array; Adding two n-bit integers by ripple carry.
	linearithmic, loglinear, or quasilinear	Performing a Fast Fourier transform; heapsort, quicksort (best and average case), or merge sort
	quadratic	Multiplying two n-digit numbers by a simple algorithm; bubble sort (worst case or naive implementation), shell sort, quicksort (worst case), selection sort or insertion sort
	polynomial or algebraic	Tree-adjoining grammar parsing; maximum matching for bipartite graphs
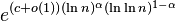	L-notation or sub-exponential	Factoring a number using the quadratic sieve or number field sieve
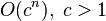	exponential	Finding the (exact) solution to the traveling salesman problem using dynamic programming; determining if two logical statements are equivalent using brute-force search
	factorial	Solving the traveling salesman problem via brute-force search; generating all unrestricted permutations of a poset; finding the determinant with expansion by minors.

1. 多种分类帮助理解排序基本概念
--内排序和外排序
--就地排序和非就地排序
--General method: insertion, exchange, selection, merging, etc.. Exchange sorts include bubble sort and quicksort. Selection sorts include shaker sort and heapsort.
2. 排序稳定性。注：不稳定的算法可以稍作修改考虑index来变成稳定的算法
3. 排序算法比较（关键是明白各个算法适用的场合）
n比较小时：选择排序
序列比较有序时：直接插入排序，冒泡排序
n比较大时：快速排序，堆排序，归并排序

（列表如下）

穩定的

• 冒泡排序（bubble sort） — O(n²)
• 鸡尾酒排序 (Cocktail sort, 雙向的冒泡排序) — O(n²)
• 插入排序 （insertion sort）— O(n²)
• 桶排序 （bucket sort）— O(n); 需要 O(k) 額外空間
• 计数排序 (counting sort) — O(n+k); 需要 O(n+k) 額外空間
• 合併排序 （merge sort）— O(n log n); 需要 O(n) 額外空間
• 原地合併排序 — O(n²)
• 二叉排序树排序 （Binary tree sort） — O(n log n)期望时间; O(n²)最坏时间; 需要 O(n) 額外空間
• 鸽巢排序 (Pigeonhole sort) — O(n+k); 需要 O(k) 額外空間
• 基數排序 （radix sort）— O(n·k); 需要 O(n) 額外空間
• Gnome 排序 — O(n²)
• 图书馆排序 — O(n log n) with high probability, 需要 (1+ε)n 額外空間

不穩定

• 選擇排序 （selection sort）— O(n²)
• 希爾排序 （shell sort）— O(n log n) 如果使用最佳的現在版本
• 组合排序 — O(n log n)
• 堆排序 （heapsort）— O(n log n)
• 平滑排序 — O(n log n)
• 快速排序 （quicksort）— O(n log n) 期望時間, O(n²) 最壞情況; 對於大的、亂數串列一般相信是最快的已知排序
• Introsort — O(n log n)
• Patience sorting — O(n log n + k) 最坏情況時間，需要 額外的 O(n + k) 空間，也需要找到最長的遞增子序列（longest increasing subsequence）

平均时间复杂度

平均时间复杂度由高到低为：

• 冒泡排序 O(n²)
• 插入排序 O(n²)
• 选择排序 O(n²)
• 归并排序 O(n log n)
• 堆排序 O(n log n)
• 快速排序 O(n log n)
• 希尔排序 O(n^1.25)
• 基数排序 O(n)

说明：虽然完全逆续的情况下，快速排序会降到选择排序的速度，不过从概率角度来说(参考信息学理论，和概率学)，不对算法做编程上优化时，快速排序的平均速度比堆排序要快一些。