冒泡排序法算法分析
冒泡排序算法的运作如下：
1.比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2.对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
3.针对所有的元素重复以上的步骤，除了最后一个。
4.持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
具体如何进行移动呢？让我们来看一个例子：
有8个数组成上面一个无序数列：5，8，6，5，9，2，1，7，目标是从小到大排序。
按照冒泡排序的思想，过程如下：
首先让5和8比较，8比5大，故两者不进行交换。
接下来8和6比较，8比6大，两者进行交换。
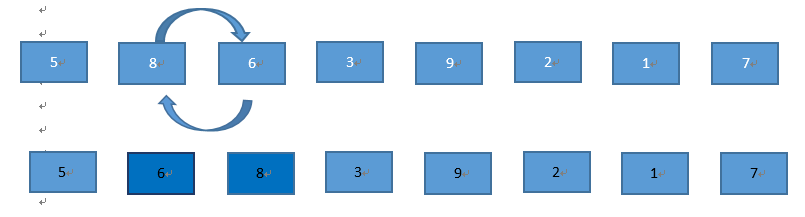
继续8和3比较，交换8和3的位置。
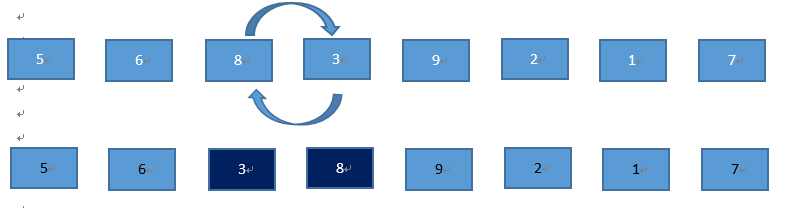
继续8和9比较，9比8大，两者不进行交换。
然后比较9和2，9比2大，两者进行交换。
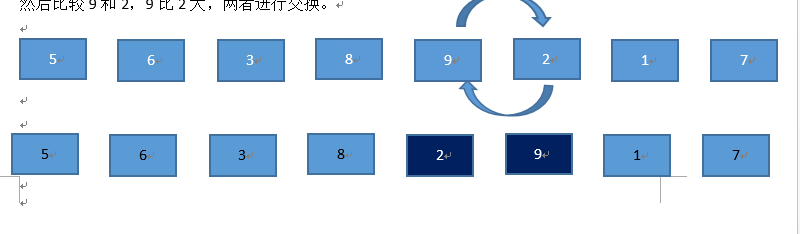
接下来比较9和1，9比1大，两者进行交换。
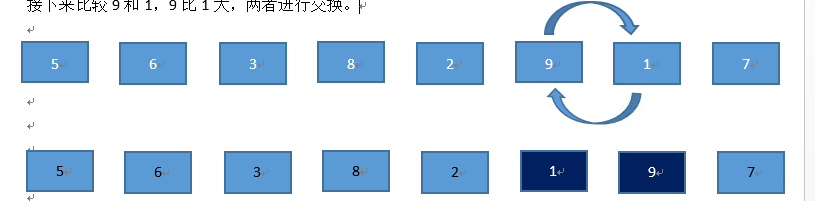
在最后比较9和7，9大于7，两者进行交换。
经过上面的冒泡排序的第一轮运作。数列最右侧元素可以认为是一个有序区域，有序区域目前只有一个元素。
接下来进行如上的7轮排序得到最终的有序数列：
第六轮、第七轮、第八轮排序:
第六轮排序：
第七轮排序：
第八轮排序：
问题分析：在6-8轮中我们待排序的数列早就已经是有序的数列的，可是冒泡排序依旧进行比较。
算法改进1：在进行每一轮的排序工作时判断数列是否有序，如已经是有序的数列则将排序工作提早结束。
算法改进2：算法改进的关键点在于对数列有序区的界定。
按照冒泡排序的逻辑，有序区的长度和排序的轮数是相等的。比如第一轮排序过后的有序长度为1，第二轮排序后有序长度是2……但是实际情况是这样子的吗？实际上，数列真正的有序区可能会大于这个长度。那么后面的许多元素的比较是没有意义的。解决思路：在每一轮排序的最后，记录下最后一个元素交换的位置，那个位置也就是无序数列的边界，再往后就是有序区了。
基本的冒泡排序代码：
//冒泡排序函数 版本1
private static void SortBubbling(int[] arr_Native) {
int temp;
for (int i = 0; i < arr_Native.length-1; i++) { //外循环只需要比较arr.length-1次就可以
for (int j = 0; j < arr_Native.length-i-1; j++) { //内循环需要比较arr_Native.length-i-1
if (arr_Native[j]>arr_Native[j+1]) {
temp=arr_Native[j];
arr_Native[j]=arr_Native[j+1];
arr_Native[j+1]=temp;
}
}
}
}
算法改进1后的代码：
//冒泡排序函数 版本2
//利用boolean变量isSored作为标记。如果在本轮排序中，元素有交换，说明数列无序；如果没有元素交换，说明数列已然有序，直接跳出大循环
private static void SortBubbling2(int[] arr_Native) {
int temp;
for (int i = 0; i < arr_Native.length-1; i++) { //外循环只需要比较arr.length-1次就可以
boolean isSored = true;
for (int j = 0; j < arr_Native.length-i-1; j++) { //内循环需要比较arr_Native.length-i-1
if (arr_Native[j]>arr_Native[j+1]) {
temp=arr_Native[j];
arr_Native[j]=arr_Native[j+1];
arr_Native[j+1]=temp;
isSored = false;
}
}
if (isSored) {
break;
}
}
}
算法改进2后的代码：
private static void SortBubbling3(int[] arr_Native) {
int temp;
//记录最后一次交换的位置
int lastExchangeIndex = 0;
//无序数列的边界，每次比较只需要比到这里为止
int sortBorder = arr_Native.length-1;
for (int i = 0; i < arr_Native.length-1; i++) { //外循环只需要比较arr.length-1次就可以
boolean isSored = true;
for (int j = 0; j < sortBorder; j++) { //内循环需要比较arr_Native.length-i-1
if (arr_Native[j]>arr_Native[j+1]) {
temp=arr_Native[j];
arr_Native[j]=arr_Native[j+1];
arr_Native[j+1]=temp;
isSored = false;
lastExchangeIndex = j;
}
}
sortBorder=lastExchangeIndex;
if (isSored) {
break;
}
}
}
