高级排序算法
1、希尔排序算法
希尔排序算法是根据它的发明者康纳德.希尔的名字命名的。此算法从根本上而言就是插入排序算法的一种改进。如同在插入排序中所做的那样,本算法的关键内容是对远距离而非相邻的数据项进行比较。当算法循环遍历数据集合的时候,每个数据项间的距离会缩短,直到算法对相邻数据项进行比较时才终止。
希尔排序算法采用升序方式对远距离的元素进行排序,序列必须从1开始,但是可以按照任意数量进行自增。一种好的可用的自增方法时基于下列代码段的:
while(h<-numElements/3); h=h*3+1;
这里的numElements表示了数据集合内代拍元素的数量,例如一个数组。
例如,如果上述代码产生的序列数是4,那么就是对数据集合内每次第4个元素进行排序,接着采用下列代码来选择一个新的序列数:
h=(h-1)/3;
然后,对后续的h个元素进行排序,一次类推。
数组类:

public class CArray { private int[] arr; private int upper; private int numElements; public CArray(int size) { arr = new int[size]; upper = size - 1; numElements = 0; } public void Insert(int item) { arr[numElements] = item; numElements++; } public void DisplayElements() { for (int i = 0; i <= upper; i++) { Console.Write($"{arr[i]} "); } Console.WriteLine("\r"); } public void Clear() { for (int i = 0; i <= upper; i++) { arr[i] = 0; } numElements = 0; } }
下面就来看一看希尔排序算法的代码。
public void ShellSort() { int inner, temp; int h = 3; while (h > 0) { for (int outer = h; outer <= numElements - 1; outer++) { temp = arr[outer]; inner = outer; while ((inner > h - 1) && arr[inner - h] >= temp) { arr[inner] = arr[inner - h]; inner -= h; } arr[inner] = temp; } h = (h - 1) % 3; } }
测试此算法的代码如下所示:
const int SIZE = 19; CArray theArray = new CArray(SIZE); Random random = new Random(); for (int index = 0; index < SIZE; index++) { theArray.Insert(random.Next(100) + 1); } Console.WriteLine(); theArray.DisplayElements(); Console.WriteLine(); theArray.ShellSort(); theArray.DisplayElements();
运行结果如下:

希尔排序算法经常被认为是一种很好的高级排序算法,这是因为它十分容易实现,甚至是对包含好几万个元素的数据集合而言其性能也是可以接受的。
2、归并排序算法
归并排序算法是一个非常好的递归算法的实例。这个算法把数据集合分成两个部分,然后对每部分递归地进行排序。当两个部分都排序好时,再用合并程序把他们组合在一起。
在堆数据集合进行排序的时候,操作十分简单。假设在数据集合内有下列这些数据:71、54、58、29、31、78、2和77。首先,这里会把数据集合分成两个独立的子集合,即子集合71、54、58、29,以及子集合31、78、2、77.接着就是对每一部分进行排序,即子集合29、54、58、71,以及子集合2、31、77、78.然后把两个子集合进行合并,即2、29、31、54、58、71、77和78。合并过程会比较两个数据子集合(存储在临时数组内)中的第一个元素,并且把较小值复制给另外一个数组。而没有被添加到第三个数组内的元素随后会与另一个数组内的下一个元素进行比较。当然还是会把较小的元素添加到第三个数组内,而且这个过程会持续到两个数组内都没有数据了为止。
但是,如果其中一个数组的元素比另外一个数组的元素先用完,那么会怎么样呢?这种情况很可能会发生,因而算法对这种情况进行了规定。在主循环结束以后,当且仅当两个数组的其中一个还留有数据时可以使用两个额外的循环用来解决这个问题。
现在就来看看执行合并排序的代码。首先是两个方法MergeSort和RecMergeSort。第一个方法简单调用了递归子程序RecMergeSort,而这个子程序对数组进行排序:
public void MergeSort() { var tempArray = new int[numElements]; RecMergeSort(tempArray, 0, numElements - 1); } public void RecMergeSort(int[] tempArray, int lbound, int ubound) { if (lbound == ubound) { return; } var mid = (int)(lbound + ubound) / 2; RecMergeSort(tempArray, lbound, mid); RecMergeSort(tempArray, mid + 1, ubound); Merge(tempArray, lbound, mid + 1, ubound); }
在RecMergeSort方法中,第一个if语句是基于递归情况的。当条件为真时,就会返回到调用它的程序。否则,就要找到数组的中间位置,并且在数组的后半部分(第一个调用RecMergeSort)递归地调用子程序,然后是在数组的前半部分(第二个调用RecMergeSort)递归地调用子程序。最终,通过调用Merge方法来把两个部分合并成在一个完整的数组。下面就是Merge方法的实现代码:
public void Merge(int[] tempArray, int lowp, int highp, int ubound) { int lbound = lowp; int mid = highp - 1; int n = (ubound - lbound) + 1; int j = 0; while ((lowp <= mid) && (highp <= ubound)) { if (arr[lowp] < arr[highp]) { tempArray[j] = arr[lowp]; j++; lowp++; } else { tempArray[j] = arr[highp]; j++; highp++; } } while (lowp <= mid) { tempArray[j] = arr[lowp]; j++; lowp++; } while (highp <= ubound) { tempArray[j] = arr[highp]; j++; highp++; } for (j = 0; j <= n - 1; j++) { arr[lbound + j] = tempArray[j]; } }
这个方法每次由RecMergeSort子程序调用来执行一个初步的排序。为了更好地实例说明这个方法时如何与RecMergeSort一起操作的,这里在Merge方法的末尾添加了这样一行代码:
this.DisplayElements();
用了这行代码,在排序完成之前就可以观察到在不同临时状态下数组的情况。输出如下图所示:

第一行显示了初始状态的数组。第二行则显示正在对数组的前半部分开始进行排序。一直到第五行,前半部分的排序才全部完成。第六行显示正在对数组的后半部分开始进行排序,而第九行显示对数组两个部分的排序都全部完成了。第十行是最终合并后的输出结果,而第十一行只是对另外一个堆ShowArray方法的调用。
3、堆排序算法
堆排序算法利用了一种被称为堆的数据结构。堆和二叉树比较类似,但是又有一些显著的差异。
3.1、堆构造
堆数据类似于二叉树,但是又不完全相同。首先,通常采用数组而不是节点引用的方式来构造堆。并且,堆有两个非常重要的条件:
1、堆必须是完整的,这就意味着每一行都必须有数据填充
2、每个节点所包含的数据要大于或等于此节点下方孩子节点们所包含的数据
下图显示了堆的一个实例:
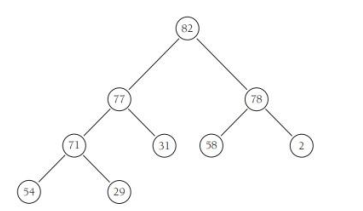
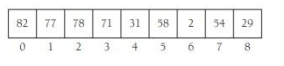
下图则说明了存储堆的数组:
存储在堆内的数据由Node类来创建。然而,这个特殊的Node类将只存储一种数据,即它的主值或者键值。这里不需要对其他节点的任何引用,但是会希望用到适合此数据的类,这样在需要的时候就可以很容易地改变存储在堆内的数据的类型。Node类的代码如下:
public class Node { public int data; public Node(int key) { data = key; } }
通过把节点插入到堆数组内的方式可以构造堆,而堆数组的元素就是堆的节点。这里始终要把新节点放置在数组末尾的空元素内。问题是这样做很可能会打破对的构造条件,因为新节点的数据值可能会大于它上面某些节点的值。为了恢复数组从而达到正确的堆构造条件,需要把新节点向上移动,一直要把它移动到数组内合适的位置上为止。这里使用被称为ShiftUp的方法来实现此操作。代码如下所示:
public class Heap { Node[] heapArray = null; private int maxSize = 0; private int currSize = 0; public Heap(int maxSize) { this.maxSize = maxSize; heapArray = new Node[maxSize]; } public bool InsertAt(int pos, Node nd) { heapArray[pos] = nd; return true; } public void ShowArray() { for (int i = 0; i < maxSize; i++) { if (heapArray[i] != null) { Console.Write(heapArray[i].data + " "); } } } }
public void ShiftUp(int index) { var parent = (index - 1) / 2; Node bottom = heapArray[index]; while ((index > 0) && (heapArray[parent].data < bottom.data)) { heapArray[index] = heapArray[parent]; index = parent; parent = (parent - 1) / 2; } heapArray[index] = bottom; }
而且下面是Insert方法的实现代码:
public bool Insert(int key) { if (currSize == maxSize) { return false; } heapArray[currSize] = new Node(key); currSize++; return true; }
这里会把新节点添加到数组的末尾。这样做会立刻打破堆构造的条件,所以通过ShiftUp方法来找到新节点在数组内的正确位置。此方法的参数就是新节点的索引。方法的第一行会计算出此节点的父节点。接着方法会把新节点保存到一个名为bottom的Node变量内。随后,while循环会找到新节点的正确位置。方法的最后一行会把新节点从临时放置的bottom内复制到数组中正确的位置上。
从堆中移除掉节点始终意味着删除最大的节点。这是很容易实现的,因为最大值始终在根节点上。问题是一旦移除掉根节点,堆就不完整了,就需要对其进行重组。下面这个算法用来使堆再次完整:
1、移除掉根节点。
2、把最后位置上的节点移动到根上。
3、把最后的节点向下移动,直到它在底下为止。
当连续应用这个算法的时候,就会按照排序顺序把数据从堆中移除掉。下面就是Remove方法和ShiftDown方法的实现代码:
public Node Remove() { Node root = heapArray[0]; currSize--; heapArray[0] = heapArray[currSize]; ShiftDown(0); return root; } public void ShiftDown(int index) { int largerChild; Node top = heapArray[index]; while (index < (int)(currSize / 2)) { int leftChild = 2 * index + 1; int rightChild = leftChild + 1; if ((rightChild < currSize) && heapArray[leftChild].data < heapArray[rightChild].data) { largerChild = rightChild; } else { largerChild = leftChild; } if (top.data >= heapArray[largerChild].data) { break; } heapArray[index] = heapArray[largerChild]; index = largerChild; } heapArray[index] = top; }
调用一下:
const int SIZE = 9; Heap heap = new Heap(SIZE); Random random = new Random(); for (int i = 0; i < SIZE; i++) { int ran = random.Next(1, 100); heap.Insert(ran); } Console.WriteLine("Random:"); heap.ShowArray(); Console.WriteLine(); Console.WriteLine("Heap:"); for (int i = (int)SIZE/2-1; i >= 0; i--) { heap.ShiftDown(i); } heap.ShowArray(); for (int i = SIZE-1; i >= 0; i--) { Node node = heap.Remove(); heap.InsertAt(i, node); } Console.WriteLine(); Console.WriteLine("Sorted:"); heap.ShowArray();

第一个for循环通过向堆内插入随机数的方式开始了构造堆的过程。第二个循环是恢复堆,而随后的第三个for循环则是用Remove方法和ShiftDown方法来重新构造有序的堆。
堆排序的效率还是蛮高的。下面要介绍的快速排序算法比此算法速度更快。
4、快速排序算法
快速排序算法的效率是实至名归的。当然这只是针对于大量且通常无序的数据集而言是正确的。如果数据集合很小(含有100个元素或者更少),或者数据是相对有序的,那么就需要采用之前介绍的基础排序算法就够了。
为了理解快速排序算法的工作原理,假设你是一名教师,现在要把一堆学生的论文按照字母顺序进行排序。你可能会选取字母表中间的一个字母,比如字母M。接着把学生名字以字母A到字母M的论文放在一起,再把学生名字以字母N到字母Z开头的论文放到另外一堆。然后你要利用相同的方法把A~M这堆再分成两堆,并且把N~Z这堆也再分成两堆。你要反复这样的操作直到所有小堆(A~C,D~F,……,X~Z)包含易于排序的两个元素或三个元素时为止。一旦所有小堆都有序了,你只需要简单地把这些小堆放在一起就会得到一个有序的论文集合。
如上你已经注意到的那样,这个过程是递归,因为每一个堆都会被分成更小的堆。一旦把堆分裂成只包含一个元素,那么这个堆就不能继续分裂了,而递归操作也就终止了。
那么人们如何决定在什么位置把数组一分为二的呢?虽然有很多种选择,但那是这里将只会选取第一个数组元素作为开始:
mv = arr[first];
快速排序算法的代码:
public void QSort() { RecQSort(0, numElements - 1); } public void RecQSort(int first, int last) { if ((last - first) <= 0) { return; } int part = this.Partition(first, last); RecQSort(first, part - 1); RecQSort(part + 1, last); } public int Partition(int first, int last) { int pivotVal = arr[first]; int theFirst = first; bool okSide; first++; do { okSide = true; while (okSide) { if (arr[first] > pivotVal) { okSide = false; } else { first++; okSide = (first <= last); } } okSide = true; while (okSide) { if (arr[last] <= pivotVal) { okSide = false; } else { last--; okSide = (first <= last); } } if (first < last) { Swap(first, last); this.DisplayElements(); first++; last--; } } while (first <= last); Swap(theFirst, last); this.DisplayElements(); return last; } public void Swap(int item1, int item2) { int temp = arr[item1]; arr[item1] = arr[item2]; arr[item2] = temp; }
快速排序算法的改进:
如果数组内的数据是随机的,俺么选取第一个数值作为“中心点”或者“分割”值是完全合理的。然后,繁殖情况做这样的选择将会降低算法的性能。
一种比较流行的选择此数值的方法时在数组内确定中间值。通过把取到的数组上限除以2的方法就可以得到这个中间值。例如:
theFirst = arr[(int)arr.GetUpperBound(0) / 2];
研究表明使用这种策略可以减少此算法运行时间的大约5个百分点。
小结
这些算法比基础排序算法在执行速度上快很多。人们普遍认为快速排序是最快的排序算法,而且应该把它用于大多数排序情况里。构建在几个.Net框架类库中的Sort方法就是用快速排序算法实现的,这就说明快速排序比其他排序算法具有优势。





