树上启发式合并学习指南

典题合集

col1	col2	col3

前置芝士

树上启发式合并(Dsu on tree)

它是用来解决一类树上询问问题，一般这种问题有两个特征。

1、只有对子树的询问

2、无修改操作，询问允许离线

启发式合并作为一种思想，表示我们在合并两个集合时，优先将小集合合并到大集合中去。这样就能够保证合并的总时间复杂度控制在nlogn以内。

[时间复杂度证明]

首先对于所有重儿子，因为重儿子是直接被继承的，因此重儿子本身只会被访问一次。当然可能这个重儿子的上面有轻边，最后还是要完全删掉，但是我们这里说的是仅仅对于父节点。我们再来看轻儿子，假如根节点到该轻儿子有k条轻边。刚开始我们会先递归到该节点上，该轻儿子本身会自己算一遍自己的答案，此时已经访问一次了。接下来他的第一条轻边的祖先的重儿子统计完后，该节点又要被访问一次。继续向上走，又遇到轻边了，一切又前功尽弃，全部删除。也就是说：每次遇到轻边，我们都要重新统计，想要统计该节点必须要访问一次。因此，对于这个节点的访问次数为：k + 1，k条轻边 + 自己算自己的。

我们考虑一个节点最多的轻边数量，假如该树有n个节点，我们希望轻边越多，那么就希望树的两边越平均即可，我们让两个子树的大小都一样，这样最后轻边的数量最多是logn，因为每次根节点要占用一个节点数量，因此轻边的数量其实是小于logn，也就是最大是：logn下去整 - 1。比如n = 16 = 2^4，我们最大的轻边数量是3，实际访问次数是3 + 1 = 4。我画个图大家就明白了：

节点数为16的树的最大轻边数量：红色表示重边，绿色表示轻边。

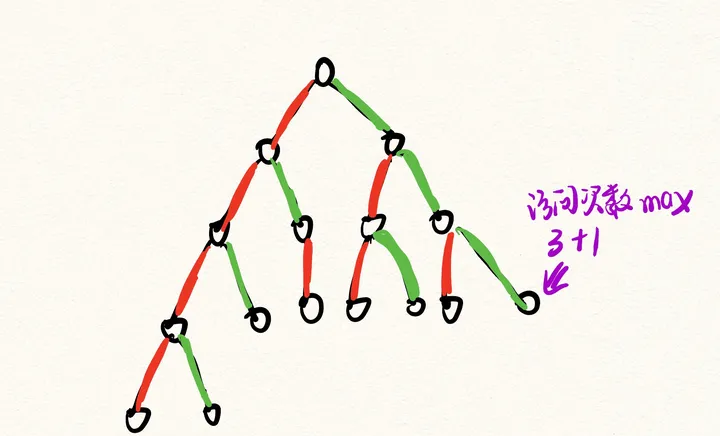
我们时间复杂度的瓶颈是被访问的次数最多的节点。但是即使是在极限数据下，也最多只有一个节点能够达到访问次数的最大值，像其他很多节点，其实被访问次数是更小的，因此时间复杂度是能够严格保证在nlogn以下的。