异或树学习指南

前置芝士

异或

树中可以形成回文的路径数

[problem description]

给你一棵 树（即，一个连通、无向且无环的图），根 节点为 0 ，由编号从 0 到 n - 1 的 n 个节点组成。这棵树用一个长度为 n 、下标从 0 开始的数组 parent 表示，其中 parent[i] 为节点 i 的父节点，由于节点 0 为根节点，所以 parent[0] == -1 。

另给你一个长度为 n 的字符串 s ，其中 s[i] 是分配给 i 和 parent[i] 之间的边的字符。s[0] 可以忽略。

找出满足 u < v ，且从 u 到 v 的路径上分配的字符可以 重新排列 形成 回文 的所有节点对 (u, v) ，并返回节点对的数目。

如果一个字符串正着读和反着读都相同，那么这个字符串就是一个 回文 。

[input]

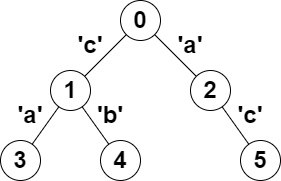
输入：parent = [-1,0,0,1,1,2], s = "acaabc"
输出：8
解释：符合题目要求的节点对分别是：
- (0,1)、(0,2)、(1,3)、(1,4) 和 (2,5) ，路径上只有一个字符，满足回文定义。
- (2,3)，路径上字符形成的字符串是 "aca" ，满足回文定义。
- (1,5)，路径上字符形成的字符串是 "cac" ，满足回文定义。
- (3,5)，路径上字符形成的字符串是 "acac" ，可以重排形成回文 "acca" 。

[datas]

• n == parent.length == s.length
• 1 <= n <= 10<sup>5</sup>
• 对于所有 i >= 1 ，0 <= parent[i] <= n - 1 均成立
• parent[0] == -1
• parent 表示一棵有效的树
• s 仅由小写英文字母组成

[solved]

1.可重排回文串等价于至多一个字母出现奇数次，其余字母出现偶数次。

2.用一个长为 26 的二进制数来压缩存储每个字母的奇偶性，只有 27个二进制数符合要求。

0表示每个字母都出现偶数次。
$2^0,21,\cdots,2^{25} $表示第 i 个字母出现奇数次，其余字母出现偶数次。

from collections import Counter
class Solution:
    def countPalindromePaths(self, parent: List[int], s: str) -> int:
        n=len(s)
        e=[[] for _ in range(n)]
        for i in range(1,n):
            e[parent[i]].append(i)
        ans=0
        cnt=Counter([0])
        def dfs(v:int,xor:int)->None:
            nonlocal ans
            for w in e[v]:
                bit=1<<(ord(s[w])-ord('a'))
                x=xor^bit
                ans+=cnt[x]+sum(cnt[x^(1<<i)] for i in range(26))
                cnt[x]+=1
                dfs(w,x)
        dfs(0,0)
        return ans

异或最小生成树