图论割点和割边学习指南
前置芝士
割点
如果去掉一个点以及与它连接的边,该点原来所在的图被分成两部分(不连通),则称该点为割点。
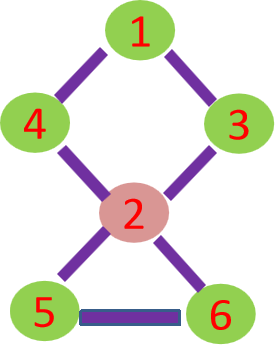
图中2号顶点就是割点
[判定]
(1)如果x不是根节点,当搜索树上存在x的一个子节点y,满足low[y]>=dfn[x],那么x就是割点。
(2)如果x是根节点,当搜索树上存在至少两个子节点y1,y2,满足上述条件,那么x就是割点。
Tarjan算法
时间复杂度:O(N+M)
如何判断割点
暴力解法:依次删除每一个顶点,然后用dfs或者bfs来检查图是否依然连通。如果删除某个顶点后,导致图不再连通,那么刚才删除的顶点就是割点。时间复杂度是O(N(N+M))。显然时间复杂度是无法接受的。
判断砍掉一个点后,连通分量的个数是否增多
(1)任选无向图中的一个点,作为树的根,然后通过dfs遍历全图。
(2)设 dfn[i] 代表节点 i 的dfs序。
注:dfs序指的是在dfs过程中,该节点是第几个被访问到的节点。显而易见的,dfn数组的值随dfs过程单调上升。
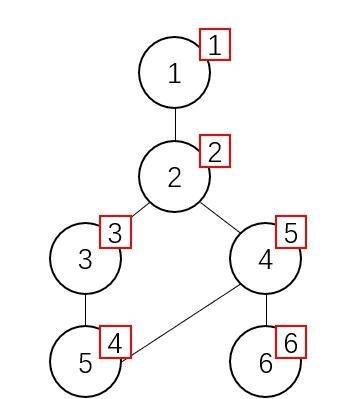
如上图,假设节点1为根节点,则节点右上角红框内的数字为其dfn。
(3)设 low[i] 代表节点 i 在不直接返回父亲节点的情况下,通过“绕路”,能够访问到的节点里,最小的dfn值。
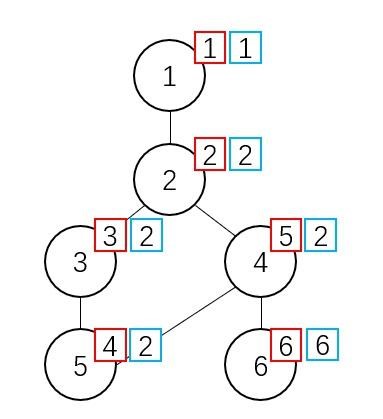
如上图,假设节点1为根节点,则节点右上角蓝框内的数字为其low。
(4)对于根节点,若其有两棵及以上的子树,则根节点为割点。
因为如果去掉根节点,两棵子树将无法互相连通。
(5)对于非根节点u,若存在一子节点v,无法通过“绕路”,访问到u除其自己外的祖先节点,则u为割点。
因为一旦去除u,u的祖先节点将与v互不连通。
此时, low[v]>=dfn[u] 。
那么,问题就转化成了如何求 low[i] 。
假设dfs过程中,当前所在节点为u,有一条边(u,v),则有如下两种情况。
①若节点v尚未访问过,则说明节点v是u的子节点。
子节点能绕路访问的dfn最小点,将对父节点做出贡献,即 low[u]=min(low[u],low[v]) 。
②若节点v已访问过,且v不是父节点,则按照dfs的规律——节点v即为某个祖先节点。故这条边是一条返祖边(又叫回边)。
此时 low[u]=min(low[u],dfn[v]) 。
①该点为根节点时,若子树数量大于一则说明该点为割点(子树数量不等于与该点连接的边数)。
②该点不为根节点时,若存在一个儿子节点的low值大于或等于该点的dfn值时( low[子节点] >= dfn[父节点] ),该点为割点(即子节点,无法通过回边,到达某一部分节点(这些节点的dfn值小于父亲节点))。
割点所割连通分量数
①设 cut[i] 表示割点 i 所割连通分量数。
②对于根节点的割点,显而易见的,它的孩子数就是所割的连通分量数,故 cut[i]=child[i] 。
③对于非根节点的割点,它所割的连通分量数为其满足条件 low[v]>=dfn[u] 的孩子数+1。因为其与父节点的连通,也会因为割点的去除而失去。
求所有割点节点
[problem description]
给出一个 \(n\) 个点,\(m\) 条边的无向图,求图的割点。
[input]
第一行输入两个正整数 \(n,m\)。
下面 \(m\) 行每行输入两个正整数 \(x,y\) 表示 \(x\) 到 \(y\) 有一条边。
[output]
第一行输出割点个数。
第二行按照节点编号从小到大输出节点,用空格隔开。
[a.in]
6 7
1 2
1 3
1 4
2 5
3 5
4 5
5 6
[a.out]
1
5
[datas]
\(1\leq n \le 2\times 10^4\),\(1\leq m \le 1 \times 10^5\)
点的编号均大于 \(0\) 小于等于 \(n\)。
tarjan图不一定联通
[solved]
const int N = 20010;
vector<int> e[N];
int n, m, res;
bool cnt[N];
int dfn[N], low[N], tot;
void tarjan(int u, int top) {
dfn[u] = low[u] = ++tot;
int child = 0;
for (auto v : e[u]) {
if (!dfn[v]) {
tarjan(v, top);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u] && u != top) {//
cnt[u] = true;
}
if (u == top) child++;
} else {
low[u] = min(low[u], dfn[v]);
}
}
if (child >= 2 && top == u) cnt[u] = true;
}
void solve() {
//freopen("a.in","r",stdin);
//freopen("a.out","w",stdout);
cin >> n >> m;
for (int i = 1, x, y; i <= m; i++) {
cin >> x >> y;
e[x].push_back(y);
e[y].push_back(x);
}
for (int i = 1; i <= n; i++) if (!dfn[i]) tarjan(i, i);
for (int i = 1; i <= n; i++) if (cnt[i]) res++;
cout << res << endl;
for (int i = 1; i <= n; i++) {
if (cnt[i]) cout << i << " ";
}
cout << endl;
}



