字符串理论学习指南

前置芝士

循环同构串

当字符串S中可以选定一个位置i满足

\[S[i\cdots n]+S[1\cdots i-1]=T \]

字符串S = “bacda”，它的循环同构"acdab"，“cdaba”，“dabac”，“abacd”.

循环遍历字符串

words="123";
words[(i + 1) % n]

最小表示法

找出字符串S的循环同构串中字典序最小的一个。

const int N = 7e5;
int n;
int s[N];//字符数组
int get_min(){
  for(int i=1;i<=n;i++) s[n+i]=s[i];
  int i = 1, j = 2, k = 0;
  while(i<=n && j<=n){
    for(k=0; k<n&&s[i+k]==s[j+k]; k++);
    s[i+k]>s[j+k] ? i=i+k+1 : j=j+k+1;
    if(i==j) j++;
  }
  return min(i, j);
}
void solve(){
  scanf("%d", &n);
  for(int i=1;i<=n;i++) scanf("%d",&s[i]);
  int k=get_min();//获取最小字符串的起始位置
  for(int i=0;i<n;i++)
    printf("%d ",s[k+i]);
}

字符串哈希

是用 进制数 的角度，把一个字符串看成是一个 p 进制的数字。

说明：每个字符有其唯一对应的 ASCII 码 ，因此在确定了 p 的取值后，能将字符串转换为数值。

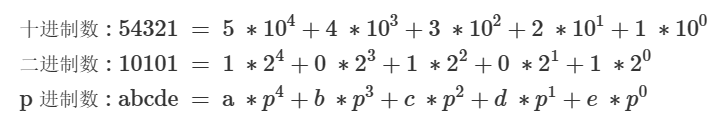
一般情况下不能将某个字母映射成 0
若 A = 0 则 AA = 0, AAA = 0, …… 这样将不同的字符串映射成了同样的数，产生错误（冲突）

[字符串哈希定义]

const int N = 100010;
const int P = 131; // 将字符串看成 P 进制的数，而这个 ( 大写 ) P 的值是自己定的 

ull h[N]; // 存储字符串每个前缀的哈希值 
ull p[N]; // 存储展开式中的权值 ( p^0, p^1 , p^2, p^3 ... ) ( 小写 p )
char str[N]; // 存储字符串

[字符串 前缀 哈希值的计算]

字符串 "abcd" 的前缀有 "a" 、"ab" 、"abc" 、"abcd"

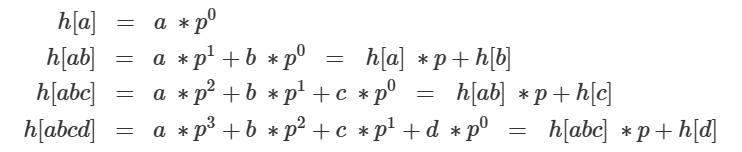
void solve(){
	scanf("%d%s",&n,str+1);
	//scanf( "%s", str + 1 ); 表示字符串是从 str[1] 开始存储的
即 str[1] 是第 1 个字符， str[2] 是第 2 个字符。
	p[0]=1;//p^0 == 1
	// h[0] == 0 ( 保持默认值即可 )，这样不会影响 h[1] 的计算
	// h[1] = h[0]*p + '1' = '1'( 1 为对应的字符 )
	for(int i=1;i<=n;i++){
	h[i]=h[i-1]*P+str[i];// 计算字符串每个 前缀 的哈希值 
	p[i]=p[i-1]*P;// 计算展开式中的各个权值 ( p^0, p^1 , p^2, p^3 ... )
	}
}

[子串哈希值]

首先类比真正的进制数 ( 以十进制为例 )

对于十进制数 987654321 ，第 1 个数为 9 ，第 2 个数为 8
要求取得区间 [ 4 , 6 ] 上的数。

从人的角度，一眼就能知道这个数 ( 子串 ) 为： 654（ 六百五十四 ）
而想要得到这个数，更严谨的做法是去掉 子串 987654 前面的 子串 987。

但计算上怎么处理呢？

若直接相减 987654 - 987 == 986667 != 654
其原因在于其中的 权重：987 不是表面的 九百八十七 ，而是 九十八万七千 。
正确的计算方法：987654 - 987000 == 654

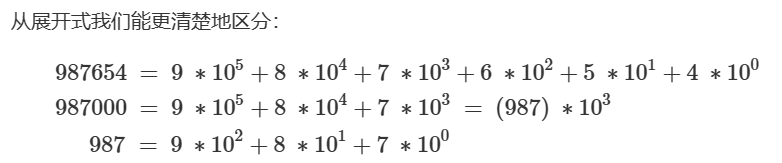
因此要提高 987 各个位的 权数 ，而这个权数与区间相关。
对于区间 [ 4 , 6 ] ，十进制数 要乘的权数为：10^( 6 - 4 + 1) == 10^3
即对于区间 [ l , r ]，p进制数 要乘的权数为：p^( r - l + 1 )

因此要提高 987 各个位的 权数 ，而这个权数与区间相关。
对于区间 [ 4 , 6 ] ，十进制数 要乘的权数为：10^( 6 - 4 + 1) == 10^3
即对于区间 [ l , r ]，p进制数 要乘的权数为：p^( r - l + 1 )

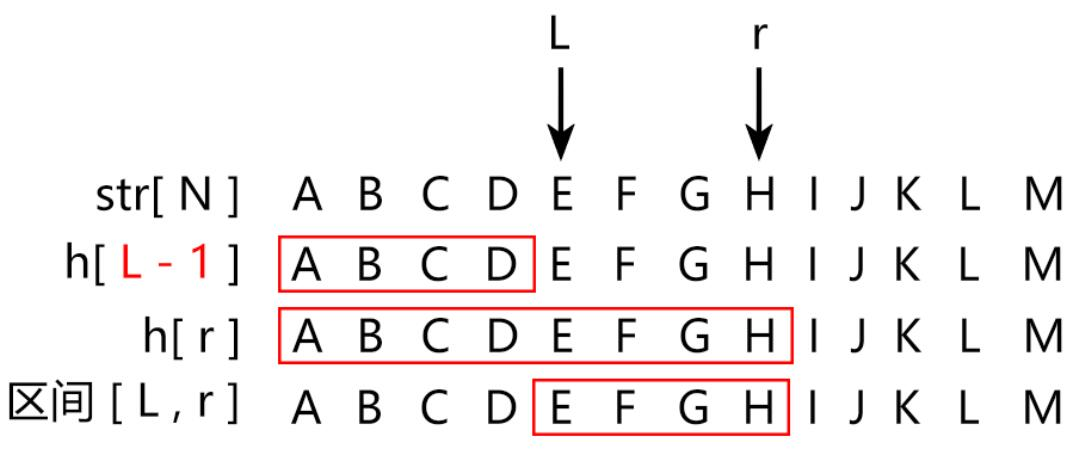
ull get( int l, int r ) // 计算区间 [ l , r ] 内字符串的哈希值 
{
    return h[r] - h[ l - 1 ] * p[ r - l + 1];
}

自然溢出法

const int P=131;
const int N=100010;
ull p[N],h[N];
string s;
void init(){
    p[0]=1,h[0]=0;
    int n=s.length();
    for(int i=1;i<=n;i++){
        p[i]=p[i-1]*P;
        h[i]=h[i-1]*P+s[i];
    }
}
ull get(int l,int r){
    return h[r]-h[l-1]*p[r-l+1];
}
bool substr(int l1,int r1,int l2,int r2){
    return get(l1,r1)==get(l2,r2);
}

回文串

Manacher算法

求出一个字符串中的最长回文串

const int N=3e7;//串长
char a[N],s[N];//a:原串,s:重构奇数串
int d[N];//加速盒子
void get_d(char *s,int n){
    d[1]=1;
    for(int i=2,l,r=1;i<=n;i++){
    if(i<=r) d[i]=min(d[r-i+l],r-i+1);//min(最长半径,盒子边界)
    while(s[i-d[i]]==s[i+d[i]]) d[i]++;//暴力求中心扩散法
    if(i+d[i]-1>r) l=i-d[i]+1,r=i+d[i]-1;//更新加速盒子
    }
}
int solve(){
    scanf("%s",a+1);
    int n=strlen(a+1),k=0;
    s[0]='$',s[++k]='#';
    for(int i=1;i<=n;i++){
        s[++k]=a[i],s[++k]='#';
    }
    n=k;
    get_d(s,n);
    int ans=0;
    for(int i=1;i<=n;i++)
        ans=max(ans,d[i]);
    //cout<<ans-1<<endl;
    return ans-1;
}

回文自动机（PAM）

kmp算法

KMP算法的核心就是next数组，有的也称为前缀表，作用就是，当模式串与主串不匹配时，指导模式串应该回退到哪个位置重新匹配。KMP相比于暴力求解，少做了无意义的比对（主串的指针是不用回退的），而是利用之前的比对结果，辅助模式串回退（遇到不匹配时），提高效率。

[前缀表]

前缀和后缀子串的最大长度。（前缀是指不包含尾字符的以第一个字符开头的所有子串，后缀是指不包含首字符的以最后一个字符结尾的所有子串）。

[next表]

next数组有多种定义，但实质是一样的，有的直接用前缀表，有的对前缀表做移位操作，有的对前缀表各位减1。

S= "babab ", 其 Next 数值序列为01123

b--------------``0 // 固定为0

ba-------------``0 // 没有相等的前缀子串和后缀子串

bab------------``1 // 前缀子串 b 和后缀子串 b 相等，故为1

baba-----------``2 // 前缀子串 ba 和后缀子串 ba 相等，故为2

babab----------``3 // 前缀子串 bab 和后缀子串 bab 相等，故为3

时间复杂度：O(n)

Z算法

后缀子串

后缀数组

模式串匹配

[problem description]

给出两个字符串 \(s_1\) 和 \(s_2\)，若 \(s_1\) 的区间 \([l, r]\) 子串与 \(s_2\) 完全相同，则称 \(s_2\) 在 \(s_1\) 中出现了，其出现位置为 \(l\)。
现在请你求出 \(s_2\) 在 \(s_1\) 中所有出现的位置。

定义一个字符串 \(s\) 的 border 为 \(s\) 的一个非 \(s\) 本身的子串 \(t\)，满足 \(t\) 既是 \(s\) 的前缀，又是 \(s\) 的后缀。
对于 \(s_2\)，你还需要求出对于其每个前缀 \(s'\) 的最长 border \(t'\) 的长度。

[input]

第一行为一个字符串，即为 \(s_1\)。
第二行为一个字符串，即为 \(s_2\)。

[output]

首先输出若干行，每行一个整数，按从小到大的顺序输出 \(s_2\) 在 \(s_1\) 中出现的位置。
最后一行输出 \(|s_2|\) 个整数，第 \(i\) 个整数表示 \(s_2\) 的长度为 \(i\) 的前缀的最长 border 长度。

[sample]

in

ABABABC
ABA

out

1
3
0 0 1

\(1 \leq |s_1|,|s_2| \leq 10^6\)，\(s_1, s_2\) 中均只含大写英文字母

[solved]

int n, m;
char s[N], p[N];
int ne[N];

void solve() {
	scanf("%s%s",s+1,p+1);
	n = strlen(s + 1), m = strlen(p + 1);
	ne[1] = 0;
	for (int i = 2, j = 0; i <= m; i++) {
		while (j && p[i] != p[j + 1]) j = ne[j];
		if (p[i] == p[j + 1]) j++;
		ne[i] = j;
	}
	for (int i = 1, j = 0; i <= n; i++) {
		while (j && s[i] != p[j + 1]) j = ne[j];
		if (s[i] == p[j + 1]) j++;
		if (j == m) printf("%d\n",i-m+1);
	}
	for (int i = 1; i <= m; i++) printf("%d ",ne[i]);
	puts("");
}