图论连通性学习指南
前置芝士
DFS生成树
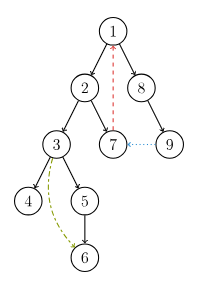
有向图的 DFS 生成树主要有 4 种边(不一定全部出现):
- 树边(tree edge):示意图中以黑色边表示,每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
- 反祖边(back edge):示意图中以红色边表示(即7->1),也被叫做回边,即指向祖先结点的边。
- 横叉边(cross edge):示意图中以蓝色边表示(即9->7),它主要是在搜索的时候遇到了一个已经访问过的结点,但是这个结点 并不是 当前结点的祖先。
- 前向边(forward edge):示意图中以绿色边表示(即3->6),它是在搜索的时候遇到子树中的结点的时候形成的。
我们考虑 DFS 生成树与强连通分量之间的关系。
如果结点 u是某个强连通分量在搜索树中遇到的第一个结点,那么这个强连通分量的其余结点肯定是在搜索树中以u为根的子树中。结点u被称为这个强连通分量的根。
反证法:假设有个结点 v在该强连通分量中但是不在以u为根的子树中,那么u到v的路径中肯定有一条离开子树的边。但是这样的边只可能是横叉边或者反祖边,然而这两条边都要求指向的结点已经被访问过了,这就和u是第一个访问的结点矛盾了。得证。
连通分量
在图论中,连通分量是指无向图中的一组顶点,其中任意两个顶点之间都存在路径。换句话说,连通分量是指图中的一个极大连通子图,即不能再添加任何其他顶点使得该子图仍然是连通的。
强连通分量
在有向图G中,如果两个顶点u,v间有一条从u到v的有向路径,同时还有一条从v到u的有向路径,则称两个顶点强连通。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向非强连通图的极大强连通子图,称为强连通分量。
极大的强连通子图
双连通分量
边双连通分量(eDcc)
边双连通分量即一个无向图中,去掉一条边后仍互相连通的极大子图。(单独的一个点也可能是一个边双连通分量)换言之,一个边双连通分量中不包含桥。
[性质]
在一个边双连通分量中,任意两点都存在至少两条互相分离的路径。
点双连通分量(vDcc)
极大的不包含割点的连通块。
求点数大于1的强连通分量
[problem description]
有一个 \(n\) 个点,\(m\) 条边的有向图,请求出这个图点数大于 \(1\) 的强连通分量个数。
[input]
第一行为两个整数 \(n\) 和 \(m\)。
第二行至 \(m+1\) 行,每一行有两个整数 \(a\) 和 \(b\),表示有一条从 \(a\) 到 \(b\) 的有向边。
[output]
仅一行,表示点数大于 \(1\) 的强连通分量个数。
\(2\le m\le 5\times 10^4\),\(1 \leq a, b \leq n\)。
[solved]
Tarjan 算法求强连通分量
在 Tarjan 算法中为每个结点 维护了以下几个变量:
1.\(dfn_u\)深度优先搜索遍历时结点u被搜索的次序。
2.在\(low_u\)的子树中能够回溯到的最早的已经在栈中的结点。设以u为根的子树为SubTree。\(low_u\)定义为以下结点的dfn的最小值:SubTree中的结点;从\(SubTree_u\)通过一条不在搜索树上的边能到达的结点。
一个结点的子树内结点的 dfn 都大于该结点的 dfn。
从根开始的一条路径上的 dfn 严格递增,low 严格非降。
按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索,维护每个结点的 dfn 与 low 变量,且让搜索到的结点入栈。每当找到一个强连通元素,就按照该元素包含结点数目让栈中元素出栈。在搜索过程中,对于结点u和与其相邻的结点v(v不是u的父节点)考虑 3 种情况:
- v未被访问:继续对v进行深度搜索。在回溯过程中,用\(low_v\)更新\(low_u\)。因为存在从u到v的直接路径,所以v能够回溯到的已经在栈中的结点,u也一定能够回溯到。
- v被访问过,已经在栈中:根据 low 值的定义,用\(dfn_v\)更新\(low_u\)。
- v被访问过,已不在栈中:说明v已搜索完毕,其所在连通分量已被处理,所以不用对其做操作。
/*
代码模板
*/
const int N=10010;
int n,m,a,b;
vector<int> e[N];
int dfn[N],low[N],idx;
int stk[N],instk[N],top;
int scc[N],siz[N],cnt;
void tarjan(int x){
//入x时,盖戳、入栈
dfn[x]=low[x]=++idx;
stk[++top]=x,instk[x]=1;
for(int y : e[x]){
if(!dfn[y]){//若y尚未访问
tarjan(y);
low[x]=min(low[x],low[y]);//回x时更新low
}
//如果已经访问过,不在栈中,说明已经组成了一个强连通分量,我们需要就将它剔除,不用更新,如果更新会导致一些节点不法出栈
else if(instk[y])//若y已访问且在栈中
low[x]=min(low[x],dfn[y]);//在x时更新low
}
//离x时,收集SCC
if(dfn[x]==low[x]){//若x是SCC的根
int y; ++cnt;
do{
y=stk[top--];
instk[y]=0;
scc[y]=cnt;//SCC编号
++siz[cnt];//SCC大小
}while(y!=x);
}
}
void solve(){
cin>>n>>m;
while(m--)
cin>>a>>b, e[a].push_back(b);
for(int i=1; i<=n; i++)//可能不连通
if(!dfn[i]) tarjan(i);
int res=0;
for(int i=1;i<=cnt;i++)
if(siz[i]>1) res++;
cout<<res<<endl;
}
边双连通分量
[problem description]
对于一个 \(n\) 个节点 \(m\) 条无向边的图,请输出其边双连通分量的个数,并且输出每个边双连通分量。
[input]
第一行,两个整数 \(n\) 和 \(m\)。
接下来 \(m\) 行,每行两个整数 \(u, v\),表示一条无向边。
[output]
第一行一个整数 \(x\) 表示边双连通分量的个数。
接下来的 \(x\) 行,每行第一个数 \(a\) 表示该分量结点个数,然后 \(a\) 个数,描述一个边双连通分量。
你可以以任意顺序输出边双连通分量与边双连通分量内的结点。
[样例输入]
5 3
1 2
2 3
1 3
[样例输出]
3
3 1 3 2
1 4
1 5
\(1 \le n \le 5 \times10 ^5\),\(1 \le m \le 2 \times 10^6\)



