前缀和学习指南
前置芝士
条件前缀和
二维前缀和
树上前缀和
点前缀和
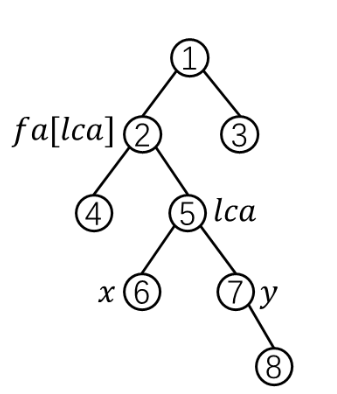
s[i]表示从根节点到节点i的点权和。
先自顶向下计算出前缀和s[i],然后用前缀和拼凑出(x,y)的路径和。
求路径和公式:
\(s[x]+s[y]-s[lca]-s[fa[lca]]\)
边前缀和
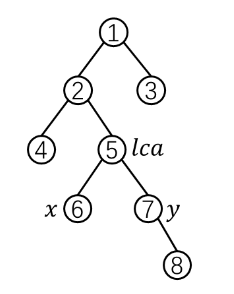
设s[i]表示从根节点到节点i的边权和。
先自顶向下计算出前缀和s[i],然后用前缀和拼凑(x,y)的路径和。
两点路径和公式:
\(s[x]+s[y]-2s[lca]\)
最大正方形
[problem description]
在一个 n×m 的只包含 0 和 1 的矩阵里找出一个不包含 0 的最大正方形,输出边长。
[input]
输入文件第一行为两个整数n,m(1≤n,m≤100),接下来 n 行,每行m 个数字,用空格隔开,0 或 1。
[output]
一个整数,最大正方形的边长。
[solved]
标准的二维前缀和模板题
求和
[problem description]
master 对树上的求和非常感兴趣。他生成了一棵有根树,并且希望多次询问这棵树上一段路径上所有节点深度的\(k\) 次方和,而且每次的\(k\) 可能是不同的。此处节点深度的定义是这个节点到根的路径上的边数。他把这个问题交给了pupil,但pupil 并不会这么复杂的操作,你能帮他解决吗?
[input]
第一行包含一个正整数\(n\),表示树的节点数。
之后\(n-1\) 行每行两个空格隔开的正整数\(i, j\),表示树上的一条连接点\(i\) 和点\(j\) 的边。
之后一行一个正整数\(m\),表示询问的数量。
之后每行三个空格隔开的正整数\(i, j, k\),表示询问从点\(i\) 到点\(j\) 的路径上所有节点深度的\(k\) 次方和。由于这个结果可能非常大,输出其对\(998244353\) 取模的结果。
树的节点从\(1\) 开始标号,其中\(1\) 号节点为树的根。
[output]
对于每组数据输出一行一个正整数表示取模后的结果。
[样例]
5
1 2
1 3
2 4
2 5
2
1 4 5
5 4 45
[样例解释]
以下用\(d (i)\) 表示第\(i\) 个节点的深度。
对于样例中的树,有\(d (1) = 0, d (2) = 1, d (3) = 1, d (4) = 2, d (5) = 2\)。
因此第一个询问答案为\((2^5 + 1^5 + 0^5)\ mod\ 998244353 = 33\),第二个询问答案为\((2^{45} + 1^{45} + 2^{45})\ mod\ 998244353 = 503245989\)。
\(1 \leq n,m \leq 300000, 1 \leq k \leq 50\)。
[solved]
倍增、树上前缀和
const ll mod = 998244353;
const int N = 3e5 + 10, M = 2 * N;
int n, m;
int h[N], to[M], ne[M], idx;
int fa[N][22];//fa[u][i]表示从u向上跳2^i层的祖先结点
int dep[N]; //dep[v]表示v的深度
ll mi[60]; //mi[j]表示dep[v]的j次幂
ll s[N][60]; //s[v][j]表示从根到v的路径节点的深度的j次幂之和
void add(int u, int v) {
to[++idx] = v, ne[idx] = h[u], h[u] = idx;
}
void dfs(int u, int f) { //预处理节点信息
for (int i = 1; i <= 20; i++)
fa[u][i] = fa[fa[u][i - 1]][i - 1];
for (int i = h[u]; i; i = ne[i]) {
int v = to[i];
if (v == f) continue;
fa[v][0] = u; dep[v] = dep[u] + 1;
for (int j = 1; j <= 50; j++) mi[j] = mi[j - 1] * dep[v] % mod;
for (int j = 1; j <= 50; j++) s[v][j] = (mi[j] + s[u][j]) % mod;
dfs(v, u);
}
}
int lca(int u, int v) { //倍增法求lca
if (dep[u] < dep[v])swap(u, v);//保证u节点的深度比v节点的深度深
for (int i = 20; i >= 0; i--)
if (dep[fa[u][i]] >= dep[v]) u = fa[u][i];
if (u == v) return v;
for (int i = 20; i >= 0; i--)
if (fa[u][i] != fa[v][i]) u = fa[u][i], v = fa[v][i];
return fa[u][0];
}
void solve() {
cin >> n;
for (int i = 1, a, b; i < n; i++) {
cin >> a >> b;
add(a, b);
add(b, a);
}
mi[0] = 1; dfs(1, 0);
cin >> m;
for (int i = 1, u, v, k; i <= m; i++) {
cin >> u >> v >> k;
int l = lca(u, v);
ll res = (s[u][k] + s[v][k] - s[l][k] - s[fa[l][0]][k] + 2 * mod) % mod;
//减去两个小于mod的数,可能造成负数,最坏的情况会有res<(-mod)的情况,(res+2*mod)%mod可以转化为正整数
cout << res << endl;
}
}
粟粟的书架
[problem description]
幸福幼儿园 B29 班的粟粟是一个聪明机灵、乖巧可爱的小朋友,她的爱好是画画和读书,尤其喜欢 Thomas H. Cormen 的文章。粟粟家中有一个 \(R\) 行 \(C\) 列的巨型书架,书架的每一个位置都摆有一本书,上数第 \(i\) 行、左数第 \(j\) 列摆放的书有 \(P_{i,j}\) 页厚。
粟粟每天除了读书之外,还有一件必不可少的工作就是摘苹果,她每天必须摘取一个指定的苹果。粟粟家果树上的苹果有的高、有的低,但无论如何凭粟粟自己的个头都难以摘到。不过她发现,如果在脚下放上几本书,就可以够着苹果;她同时注意到,对于第 \(i\) 天指定的那个苹果,只要她脚下放置书的总页数之和不低于 \(H_i\),就一定能够摘到。
由于书架内的书过多,父母担心粟粟一天内就把所有书看完而耽误了上幼儿园,于是每天只允许粟粟在一个特定区域内拿书。这个区域是一个矩形,第 \(i\) 天给定区域的左上角是上数第\(x1_i\) 行的左数第 \(y1_i\) 本书,右下角是上数第 \(x2_i\) 行的左数第 \(y2_i\) 本书。换句话说,粟粟在这一天,只能在这 \((x2_i-x1_i+1)\times(y2_i-y1_i+1)\) 本书中挑选若干本垫在脚下,摘取苹果。
粟粟每次取书时都能及时放回原位,并且她的书架不会再撤下书目或换上新书,摘苹果的任务会一直持续 \(M\) 天。给出每本书籍的页数和每天的区域限制及采摘要求,请你告诉粟粟,她每天至少拿取多少本书,就可以摘到当天指定的苹果。
[input]
第一行是三个正整数 \(R, C, M\)。
接下来是一个 \(R\) 行 \(C\) 列的矩阵,从上到下、从左向右依次给出了每本书的页数 \(P_{i,j}\)。
接下来 \(M\) 行,第 \(i\) 行给出正整数 \(x1_i, y1_i, x2_i, y2_i, H_i\),表示第 \(i\) 天的指定区域是 \((x1_i, y1_i)\) 与 \((x2_i, y2_i)\) 间的矩形,总页数之和要求不低于Hi。
保证 \(1\le x1_i\le x2_i\le R\),\(1\le y1_i\le y2_i\le C\)。
[output]
输出共 \(M\) 行,第 \(i\) 行回答粟粟在第 \(i\) 天时为摘到苹果至少需要拿取多少本书。如果即使取走所有书都无法摘到苹果,则在该行输出 Poor QLW。
[sample]
in
5 5 7
14 15 9 26 53
58 9 7 9 32
38 46 26 43 38
32 7 9 50 28
8 41 9 7 17
1 2 5 3 139
3 1 5 5 399
3 3 4 5 91
4 1 4 1 33
1 3 5 4 185
3 3 4 3 23
3 1 3 3 108
out
6
15
2
Poor QLW
9
1
3
[datas]
对于 \(50\%\) 的数据,满足 \(R, C\le 200\),\(M\le 2\times 10^5\)
\(1\le P_{i,j}\le 1000\),\(1\le H_i\le 2\times 10^9\)
[solved]
(1)这是一道组合算法题,在这里我关注于work1的算法过程
(2)预处理二维前缀和,二分书页范围,判定答案。
const int N = 500005;
int n, m, q;
int a[210][210], f[210][210][1010], g[210][210][1010];
//f[i][j][k]:区间[(1,1),(i,j)]内>=k的书的总页数
//f[i][j][k]:区间[(1,1),(i,j)]内>=k的总个数
int getsum(int x1, int y1, int x2, int y2, int k, int t) {
if (t) return f[x2][y2][k] - f[x2][y1 - 1][k] - f[x1 - 1][y2][k] + f[x1 - 1][y1 - 1][k];
else return g[x2][y2][k] - g[x2][y1 - 1][k] - g[x1 - 1][y2][k] + g[x1 - 1][y1 - 1][k];
}
void work1() {
int mx = -1e9;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j];
mx = max(a[i][j], mx);
}
}
for (int k = 1; k <= mx; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
f[i][j][k] = f[i - 1][j][k] + f[i][j - 1][k] - f[i - 1][j - 1][k] + (a[i][j] >= k) * a[i][j];
g[i][j][k] = g[i - 1][j][k] + g[i][j - 1][k] - g[i - 1][j - 1][k] + (a[i][j] >= k);
}
}
}
// cout<<getsum(1,1,2,2,1,0)<<endl;
int x1, y1, x2, y2, h;
for (int i = 1; i <= q; i++) {
cin >> x1 >> y1 >> x2 >> y2 >> h;
if (getsum(x1, y1, x2, y2, 1, 1) < h) {cout << "Poor QLW" << endl; continue;}
int l = 0, r = mx + 1;
while (l + 1 < r) {
int mid = (l + r) >> 1; //二分书页范围[1,mx]
if (getsum(x1, y1, x2, y2, mid, 1) >= h) {
l = mid;
} else {
r = mid;
}
}
cout << getsum(x1, y1, x2, y2, l, 0) - (getsum(x1, y1, x2, y2, l, 1) - h) / l << endl;
}
}
int b[N], root[N], tot; //root根节点,tot节点个数
int ls[N * 25], rs[N * 25], sum[N * 25], siz[N * 25];
//sum:区间内书的总页数
//siz:区间内书的总个数
void change(int &u, int v, int l, int r, int x) { //点修
u = ++tot; //动态开点
ls[u] = ls[v]; rs[u] = rs[v]; sum[u] = sum[v] + x; siz[u] = siz[v] + 1;
if (l == r)return; //二分书页范围[1,mx]
int mid = (l + r) >> 1;
if (x <= mid)change(ls[u], ls[u], l, mid, x);
else change(rs[u], rs[u], mid + 1, r, x);
}
int query(int u, int v, int l, int r, int h) { //点查
if (l == r)return (h + l - 1) / l;
int s = sum[rs[u]] - sum[rs[v]]; //二分书页范围[1,mx]
int mid = (l + r) >> 1;
if (h <= s)return query(rs[u], rs[v], mid + 1, r, h);
else return query(ls[u], ls[v], l, mid, h - s) + siz[rs[u]] - siz[rs[v]];
}
void work2() { //可持久化线段树
int mx = -1e9;
for (int i = 1; i <= m; i++) cin >> b[i], mx = max(mx, b[i]);
for (int i = 1; i <= m; i++)change(root[i], root[i - 1], 1, mx, b[i]);
for (int i = 1, x1, y1, x2, y2, h; i <= q; i++) {
cin >> x1; cin >> y1, y1 = root[y1-1]; cin >> x2; cin >> y2, y2 = root[y2]; cin >> h;
if (sum[y2] - sum[y1] < h) {cout << "Poor QLW" << endl; continue;}
cout << query(y2, y1, 1, mx, h) << endl;
}
}
void solve() {
cin >> n >> m >> q;
if (n > 1) {
work1();
} else {
work2();
}
}


