[labuladong算法小抄]手把手带你刷二叉树（第一期）
本文摘自labuladong算法小抄 ， 使用go语言描述
我们公众号的成名之作 学习数据结构和算法的框架思维 中多次强调，先刷二叉树的题目，先刷二叉树的题目，先刷二叉树的题目，因为很多经典算法，以及我们前文讲过的所有回溯、动归、分治算法，其实都是树的问题，而树的问题就永远逃不开树的递归遍历框架这几行破代码：
/* 二叉树遍历框架 */ func traverse(root *TreeNode) { // 前序遍历 traverse(root.left) // 中序遍历 traverse(root.right) // 后序遍历 }
上篇公众号文章让读者留言说说对什么问题还有疑惑，我接下来可以重点写一写相关的文章。结果还有很多读者说觉得「递归」非常难以理解，说实话，递归解法应该是最简单，最容易理解的才对，行云流水地写递归代码是学好算法的基本功，而二叉树相关的题目就是最练习递归基本功，最练习框架思维的。
我先花一些篇幅说明二叉树算法的重要性。
一、二叉树的重要性
举个例子，比如说我们的经典算法「快速排序」和「归并排序」，对于这两个算法，你有什么理解？如果你告诉我，快速排序就是个二叉树的前序遍历，归并排序就是个二叉树的后序遍历，那么我就知道你是个算法高手了。
为什么快速排序和归并排序能和二叉树扯上关系？我们来简单分析一下他们的算法思想和代码框架：
快速排序的逻辑是，若要对 nums[lo..hi] 进行排序，我们先找一个分界点 p，通过交换元素使得 nums[lo..p-1] 都小于等于 nums[p]，且 nums[p+1..hi] 都大于 nums[p]，然后递归地去 nums[lo..p-1] 和 nums[p+1..hi] 中寻找新的分界点，最后整个数组就被排序了。
快速排序的代码框架如下：
func sort(nums *[]int ,lo int ,hi int ) { /****** 前序遍历位置 ******/ // 通过交换元素构建分界点 p p := partition(nums, lo, hi) /************************/ sort(nums, lo, p - 1) sort(nums, p + 1, hi) }
先构造分界点，然后去左右子数组构造分界点，你看这不就是一个二叉树的前序遍历吗？
再说说归并排序的逻辑，若要对 nums[lo..hi] 进行排序，我们先对 nums[lo..mid] 排序，再对 nums[mid+1..hi] 排序，最后把这两个有序的子数组合并，整个数组就排好序了。
归并排序的代码框架如下：
func sort(nums int[] ,lo int , hi int ) { mid := (lo + hi) / 2 sort(nums, lo, mid); sort(nums, mid + 1, hi) /****** 后序遍历位置 ******/ // 合并两个排好序的子数组 merge(nums, lo, mid, hi) /************************/ }
先对左右子数组排序，然后合并（类似合并有序链表的逻辑），你看这是不是二叉树的后序遍历框架？另外，这不就是传说中的分治算法嘛，不过如此呀。
如果你一眼就识破这些排序算法的底细，还需要背这些算法代码吗？这不是手到擒来，从框架慢慢扩展就能写出算法了。
说了这么多，旨在说明，二叉树的算法思想的运用广泛，甚至可以说，只要涉及递归，都可以抽象成二叉树的问题，所以本文和后续的 手把手带你刷二叉树（第二期） 以及 手把手刷二叉树（第三期），我们直接上几道比较有意思，且能体现出递归算法精妙的二叉树题目，东哥手把手教你怎么用算法框架搞定它们
二、写递归算法的秘诀
我们前文 二叉树的最近公共祖先 写过，写递归算法的关键是要明确函数的「定义」是什么，然后相信这个定义，利用这个定义推导最终结果，绝不要跳入递归的细节。
怎么理解呢，我们用一个具体的例子来说，比如说让你计算一棵二叉树共有几个节点：
// 定义：count(root) 返回以 root 为根的树有多少节点 func count(root *TreeNode)int { // base case if root == nil{ return 0 } // 自己加上子树的节点数就是整棵树的节点数 return 1 + count(root.left) + count(root.right) }
这个问题非常简单，大家应该都会写这段代码，root 本身就是一个节点，加上左右子树的节点数就是以 root 为根的树的节点总数。
左右子树的节点数怎么算？其实就是计算根为 root.left 和 root.right 两棵树的节点数呗，按照定义，递归调用 count 函数即可算出来。
写树相关的算法，简单说就是，先搞清楚当前 root 节点该做什么，然后根据函数定义递归调用子节点，递归调用会让孩子节点做相同的事情。
我们接下来看几道算法题目实操一下。
三、算法实践
第一题、翻转二叉树
我们先从简单的题开始，看看力扣第 226 题「翻转二叉树」，输入一个二叉树根节点 root，让你把整棵树镜像翻转，比如输入的二叉树如下：
4
/ \
2 7
/ \ / \
1 3 6 9算法原地翻转二叉树，使得以 root 为根的树变成：
4
/ \
7 2
/ \ / \
9 6 3 1通过观察，我们发现只要把二叉树上的每一个节点的左右子节点进行交换，最后的结果就是完全翻转之后的二叉树。
可以直接写出解法代码：
// 将整棵树的节点翻转 func invertTree(root *TreeNode )*TreeNode { // base case if root == nil { return nil } /**** 前序遍历位置 ****/ // root 节点需要交换它的左右子节点 tmp := root.left root.left = root.right root.right = tmp // 让左右子节点继续翻转它们的子节点 invertTree(root.left) invertTree(root.right) return root }
这道题目比较简单，关键思路在于我们发现翻转整棵树就是交换每个节点的左右子节点，于是我们把交换左右子节点的代码放在了前序遍历的位置。
值得一提的是，如果把交换左右子节点的代码放在后序遍历的位置也是可以的，但是放在中序遍历的位置是不行的，请你想一想为什么？这个应该不难想到，我会把答案置顶在公众号留言区。
首先讲这道题目是想告诉你，二叉树题目的一个难点就是，如何把题目的要求细化成每个节点需要做的事情。
这种洞察力需要多刷题训练，我们看下一道题。
第二题、填充二叉树节点的右侧指针
这是力扣第 116 题，看下题目：
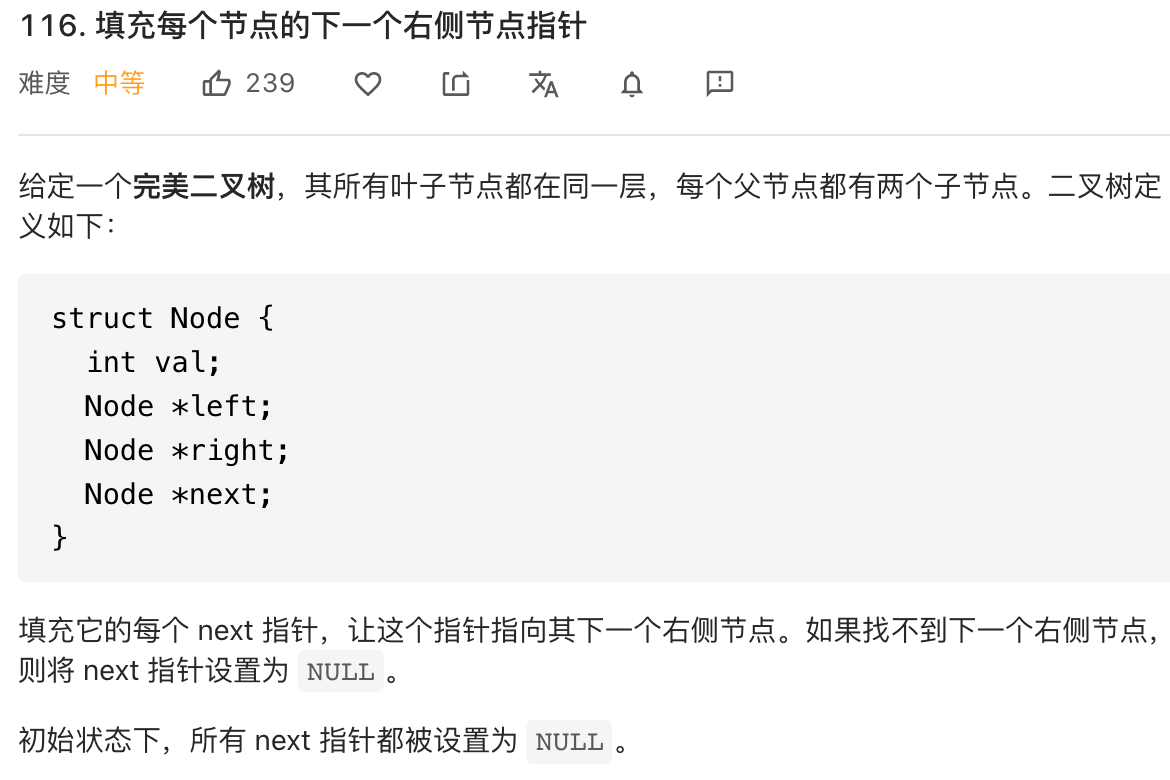
func connect(root *Node)*Node
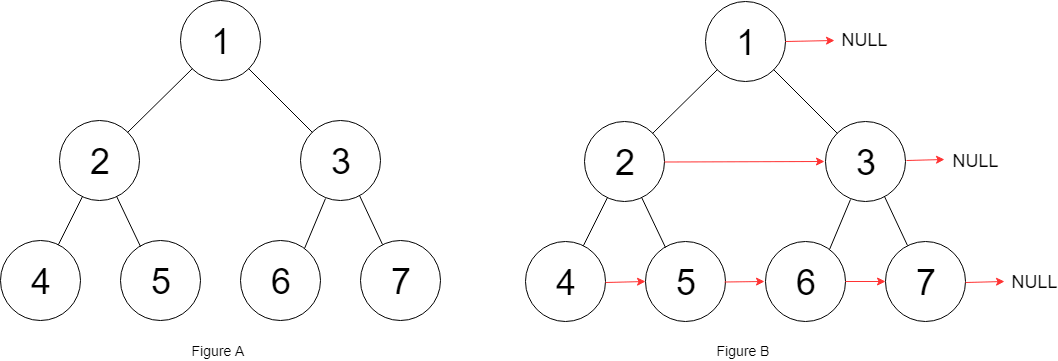
而且题目说了，输入是一棵「完美二叉树」，形象地说整棵二叉树是一个正三角形，除了最右侧的节点 next 指针会指向 null，其他节点的右侧一定有相邻的节点。
这道题怎么做呢？把每一层的节点穿起来，是不是只要把每个节点的左右子节点都穿起来就行了？
我们可以模仿上一道题，写出如下代码：
func connect(root *Node)*Node{ if root == nil || root.left == nil { return root } root.left.next = root.right connect(root.left) connect(root.right) return root }
这样其实有很大问题，再看看这张图：
节点 5 和节点 6 不属于同一个父节点，那么按照这段代码的逻辑，它俩就没办法被穿起来，这是不符合题意的。
回想刚才说的，二叉树的问题难点在于，如何把题目的要求细化成每个节点需要做的事情，但是如果只依赖一个节点的话，肯定是没办法连接「跨父节点」的两个相邻节点的。
那么，我们的做法就是增加函数参数，一个节点做不到，我们就给他安排两个节点，「将每一层二叉树节点连接起来」可以细化成「将每两个相邻节点都连接起来」：
// 主函数 func connect2(root *Node ) *Node{ if root == nil{ return nil } connectTwoNode(root.left, root.right) return root } // 辅助函数 func connectTwoNode(node1 *Node, node2 *Node){ if node1 == nil || node2 == nil{ return } /**** 前序遍历位置 ****/ // 将传入的两个节点连接 node1.next = node2 // 连接相同父节点的两个子节点 connectTwoNode(node1.left, node1.right) connectTwoNode(node2.left, node2.right) // 连接跨越父节点的两个子节点 connectTwoNode(node1.right, node2.left) }
这样，connectTwoNode 函数不断递归，可以无死角覆盖整棵二叉树，将所有相邻节点都连接起来，也就避免了我们之前出现的问题，这道题就解决了。
