Java 的八种排序算法
Java 的八种排序算法
这个世界，需要遗忘的太多。
背景：工作三年，算法一问三不知。
一、八种排序算法
直接插入排序、希尔排序、简单选择排序、堆排序、冒泡排序、快速排序、归并排序和基数排序。
二、算法使用
1 直接插入排序
使用场景：
如把新的数据插入到已排好的数据列中。
实现思想：
a、将第一个数和第二个数排序，然后构成一个有序序列；
b、将第三个数插入进去，构成一个新的有序序列；
c、对第四个数、第五个数……直到最后一个数，重复第二步。
代码实现：
1 /**
2 * @author tjt
3 * @time 2020-09-02
4 * Java 排序算法
5 */
6 public class JavaSortAlgorithm {
7
8
9 /**
10 * 直接插入排序：
11 * 首先，设定插入次数，即循环次数，for(int i=1;i<length;i++)，第1个数的那次不用插入，会有元素间的比较排序
12 * 然后，设定插入数和得到已经排好序列的最后一个数的位数：insertNum和j=i-1
13 * 从最后一个数开始向前循环，如果插入数小于当前数，就将当前数向后移动一位
14 * 将当前数放置到空着的位置，即j+1。
15 *
16 * @param array
17 */
18 private static void justInsertSort(int[] array) {
19 System.out.println("***********直接插入排序*************");
20 int length = array.length;
21 // insertNum 为要插入的数
22 int insertNum;
23 for (int i = 1; i < length; i++) {
24 insertNum = array[i];
25 System.out.println("insertNum: " + insertNum);
26 // 已经排序好的序列元素个数
27 int j = i - 1;
28 System.out.println(Arrays.toString(array));
29 // 序列从后到前循环，将大于insertNum 的数向后移动一格
30 while (j >= 0 && array[j] > insertNum) {
31 // 元素移动一格
32 array[j + 1] = array[j];
33 // j-- 之后继续于之前的比较，从后往前
34 j--;
35 }
36 // 将需要插入的数放在要插入的位置。
37 array[j + 1] = insertNum;
38 }
39 }
40
41 }
直接插入排序结果验证：
2 希尔排序
使用场景：
对于直接插入排序问题，数据量巨大时，可以考虑使用希尔排序。
实现思想：
a、将数的个数设为n，取奇数k=n/2，将下标差值为k 的树分为一组，构成有序序列；
b、再取k=k/2 ，将下标差值为k 的数分为一组，构成有序序列；
c、重复第二步，直到k=1 执行简单插入排序。
代码实现：
1 /**
2 * 希尔排序：
3 * 首先，确定分的组数，然后对组中元素进行插入排序
4 * 接下来，将length/2，重复1,2步，直到length=0 为止。
5 *
6 * @param array
7 */
8 private static void xiErSort(int[] array) {
9 System.out.println("***********希尔排序*************");
10 int length = array.length;
11 while (length != 0) {
12 length = length / 2;
13 // 分的数组
14 for (int x = 0; x < length; x++) {
15 // 组中的元素，从第二个数开始
16 for (int i = x + length; i < array.length; i += length) {
17 // j为有序序列最后一位的位数
18 int j = i - length;
19 // temp 为要插入的元素
20 int temp = array[i];
21 // 从后往前遍历
22 for (; j >= 0 && temp < array[j]; j -= length) {
23 // 向后移动length 位
24 array[j + length] = array[j];
25 }
26 array[j + length] = temp;
27 }
28 }
29 }
30 }
希尔排序结果验证：
3 简单选择排序
使用场景：
常用于取序列中最大最小的几个数。(如果每次比较都交换，那么就是交换排序；如果每次比较完一个循环再交换，就是简单选择排序。)
实现思想：
a、遍历整个序列，将最小的数放在最前面；
b、遍历剩下的序列，将最小的数放在最前面；
c、重复第二步，直到只剩下一个数。
代码实现：
1 /**
2 * 简单选择排序：
3 * 首先确定循环次数，并且记住当前数字和当前位置。
4 * 将当前位置后面所有的数与当前数字进行对比，小数赋值给key，并记住小数的位置。
5 * 比对完成后，将最小的值与第一个数的值交换。
6 * 重复2、3步。
7 *
8 * @param array
9 */
10 private static void simpleSelectSort(int[] array) {
11 System.out.println("***********简单选择排序*************");
12 int length = array.length;
13 // 循环次数
14 for (int i = 0; i < length; i++) {
15 int key = array[i];
16 int position = i;
17 // 选出最小的值和位置
18 for (int j = i + 1; j < length; j++) {
19 if (array[j] < key) {
20 key = array[j];
21 position = j;
22 }
23 }
24 // 交换位置
25 array[position] = array[i];
26 array[i] = key;
27 }
28 }
简单选择排序结果验证：
4 堆排序
使用场景：
堆排序使用场景与简单排序相似，其是简单排序的优化。
实现思想：
a、将序列构建成大顶堆；
b、将根节点与最后一个节点交换，然后断开最后一个节点；
c、重复第一、二步，直到所有节点断开。
代码实现：
1 /**
2 * 堆排序：
3 * 将序列构建成大顶堆；
4 * 将根节点与最后一个节点交换，然后断开最后一个节点；
5 * 重复第一、二步，直到所有节点断开。
6 *
7 * @param array
8 */
9 public static void heapSort(int[] array) {
10 System.out.println("***********堆排序*************");
11 System.out.println("开始排序：");
12 int arrayLength = array.length;
13 // 循环建堆
14 for (int i = 0; i < arrayLength - 1; i++) {
15 // 建堆
16 buildMaxHeap(array, arrayLength - 1 - i);
17 // 交换堆顶和最后一个元素
18 swap(array, 0, arrayLength - 1 - i);
19 System.out.println(Arrays.toString(array));
20 }
21 }
堆排序结果验证：
5 冒泡排序
使用场景：
一般比较少使用冒泡排序，徐工说会哥冒泡排序出去面试就有15K。
实现思想：
a、将序列中所有元素两两比较，将最大的放在最后面。
b、将剩余序列中所有元素两两比较，将最大的放在最后面。
c、重复第二步，直到只剩下一个数
代码实现：
1 /**
2 * 冒泡排序：
3 * 设置循环次数。
4 * 设置开始比较的位数，和结束的位数。
5 * 两两比较，将最小的放到前面去。
6 * 重复2、3步，直到循环次数完毕。
7 *
8 * @param array
9 */
10 private static void bubbleSort(int[] array) {
11 int length = array.length;
12 int temp;
13 for (int i = 0; i < length; i++) {
14 for (int j = 0; j < length - i - 1; j++) {
15 if (array[j] > array[j + 1]) {
16 temp = array[j];
17 array[j] = array[j + 1];
18 array[j + 1] = temp;
19 }
20 }
21 }
22 }
冒泡排序结果验证：
6 快速排序
使用场景：
对排序时间要求较高的情况下可以考虑使用快排。
实现思想：
a、选择第一个数为p，小于p的数放在左边，大于p的数放在右边；
b、递归的将p左边和右边的数都按照第一步进行，直到不能递归。
代码实现：
1 /**
2 * 快速排序：
3 * 选择第一个数为p，小于p的数放在左边，大于p的数放在右边；
4 * 递归的将p左边和右边的数都按照第一步进行，直到不能递归。
5 *
6 * @param array
7 * @param start
8 * @param end
9 */
10 private static void quicklySort(int[] array, int start, int end) {
11 System.out.println("***********快速排序*************");
12 if (start < end) {
13 // 选定的基准值（第一个数值作为基准值）
14 int base = array[start];
15 // 记录临时中间值
16 int temp;
17 int i = start, j = end;
18 do {
19 while ((array[i] < base) && (i < end)) {
20 i++;
21 }
22 while ((array[j] > base) && (j > start)) {
23 j--;
24 }
25 if (i <= j) {
26 temp = array[i];
27 array[i] = array[j];
28 array[j] = temp;
29 i++;
30 j--;
31 }
32 } while (i <= j);
33 if (start < j) {
34 quicklySort(array, start, j);
35 }
36 if (end > i) {
37 quicklySort(array, i, end);
38 }
39 }
40 }
快速排序结果验证：
7 归并排序
使用场景：
速度仅次于快排，在内存少的时候使用、可以进行并行计算的时候使用。
实现思想：
a、选择相邻两个数组成一个有序序列；
b、选择相邻的两个有序序列组成一个有序序列；
c、重复第二步，直到全部组成一个有序序列。
代码实现：
1 /**
2 * 归并排序：
3 * 选择相邻两个数组成一个有序序列；
4 * 选择相邻的两个有序序列组成一个有序序列；
5 * 重复第二步，直到全部组成一个有序序列。
6 *
7 * @param arr
8 * @param l
9 * @param r
10 */
11 private static void mergeSort(int[] arr, int l, int r) {
12 System.out.println("***********归并排序*************");
13 if (l < r) {
14 int q = (l + r) / 2;
15 mergeSort(arr, l, q);
16 mergeSort(arr, q + 1, r);
17 merge(arr, l, q, r);
18 }
19 }
20
21 /**
22 * @param arr 排序数组
23 * @param l 数组最左边下标
24 * @param q 数组中间位置下标
25 * @param r 数组最右位置下标
26 */
27 private static void merge(int[] arr, int l, int q, int r) {
28 /**
29 * 因为每次切割后左边下标都是（l,q），右边数组的下标是(q+1,r)
30 * 所以左边数组的元素个数就是q - l + 1
31 * 右边的数组元素个数就是r - q
32 */
33 // 切割后左边数组的数据长度
34 final int n1 = q - l + 1;
35 // 切割后右边数组的数据长度
36 final int n2 = r - q;
37 /**创建两个新数组将切割后的数组分别放进去，长度加1是为了放置无穷大的数据标志位**/
38 // 加一操作是增加无穷大标志位
39 final int[] left = new int[n1 + 1];
40 // 加一操作是增加无穷大标志位
41 final int[] right = new int[n2 + 1];
42 //两个循环将数据添加至新数组中
43 /**左边的数组下标是从l到q**/
44 /**遍历左边的数组*/
45 for (int i = 0; i < n1; i++) {
46 left[i] = arr[l + i];
47 }
48 for (int i = 0; i < n2; i++) {
49 right[i] = arr[q + 1 + i];
50 }
51
52 // 将最大的正整数放在两个新数组的最后一位
53 left[n1] = Integer.MAX_VALUE;
54 right[n2] = Integer.MAX_VALUE;
55
56 int i = 0, j = 0;
57 // 将小的放在前面
58 for (int k = l; k <= r; k++) {
59 if (left[i] <= right[j]) {
60 arr[k] = left[i];
61 i = i + 1;
62 } else {
63 arr[k] = right[j];
64 j = j + 1;
65 }
66 }
67 }
归并排序结果验证：
8 基数排序
使用场景：
适用于数目量较大、很长的数进行排序。（排序队列存在负数除外）
实现思想：
a、将所有的数的个位数取出，按照个位数进行排序，构成一个序列；
b、将新构成的所有的数的十位数取出，按照十位数进行排序，构成一个序列。
代码实现：
1 /**
2 * 基数排序：
3 * 将所有的数的个位数取出，按照个位数进行排序，构成一个序列；
4 * 将新构成的所有的数的十位数取出，按照十位数进行排序，构成一个序列。
5 *
6 * @param array 排序队列中存在负数除外
7 */
8 private static void baseSort(int[] array) {
9 System.out.println("***********基数排序*************");
10 // 首先确定排序的趟数;
11 int max = array[0];
12 for (int i = 1; i < array.length; i++) {
13 if (array[i] > max) {
14 max = array[i];
15 }
16 }
17 int time = 0;
18 // 判断位数;
19 while (max > 0) {
20 max /= 10;
21 time++;
22 }
23 // 建立10个队列;
24 List<ArrayList> queue = new ArrayList<ArrayList>();
25 for (int i = 0; i < 10; i++) {
26 ArrayList<Integer> queue1 = new ArrayList<Integer>();
27 queue.add(queue1);
28 }
29 // 进行time次分配和收集;
30 for (int i = 0; i < time; i++) {
31 //分配数组元素;
32 for (int j = 0; j < array.length; j++) {
33 // 得到数字的第time+1位数;
34 int x = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
35 ArrayList<Integer> queue2 = queue.get(x);
36 queue2.add(array[j]);
37 queue.set(x, queue2);
38 }
39 // 元素计数器;
40 int count = 0;
41 // 收集队列元素;
42 for (int k = 0; k < 10; k++) {
43 while (queue.get(k).size() > 0) {
44 ArrayList<Integer> queue3 = queue.get(k);
45 array[count] = queue3.get(0);
46 queue3.remove(0);
47 count++;
48 }
49 }
50 }
51 }
基数排序结果验证：
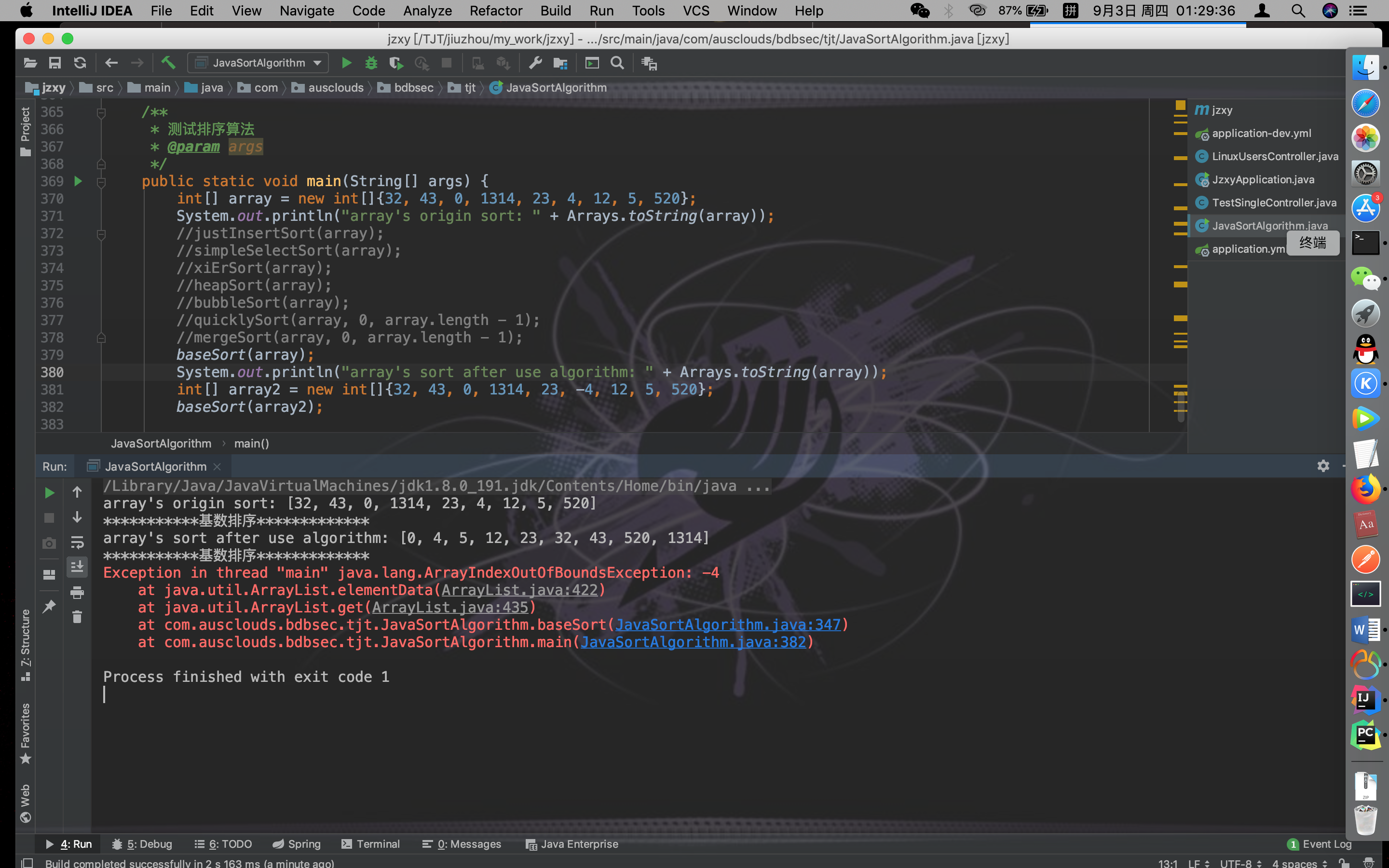
八种排序算法代码：
1 package com.ausclouds.bdbsec.tjt;
2
3 import java.util.ArrayList;
4 import java.util.Arrays;
5 import java.util.List;
6
7 /**
8 * @author tjt
9 * @time 2020-09-02
10 * Java 排序算法
11 */
12 public class JavaSortAlgorithm {
13
14
15 /**
16 * 直接插入排序：
17 * 首先，设定插入次数，即循环次数，for(int i=1;i<length;i++)，第1个数的那次不用插入，会有元素间的比较排序
18 * 然后，设定插入数和得到已经排好序列的最后一个数的位数：insertNum和j=i-1
19 * 从最后一个数开始向前循环，如果插入数小于当前数，就将当前数向后移动一位
20 * 将当前数放置到空着的位置，即j+1。
21 *
22 * @param array
23 */
24 private static void justInsertSort(int[] array) {
25 System.out.println("***********直接插入排序*************");
26 int length = array.length;
27 // insertNum 为要插入的数
28 int insertNum;
29 for (int i = 1; i < length; i++) {
30 insertNum = array[i];
31 System.out.println("insertNum: " + insertNum);
32 // 已经排序好的序列元素个数
33 int j = i - 1;
34 System.out.println(Arrays.toString(array));
35 // 序列从后到前循环，将大于insertNum 的数向后移动一格
36 while (j >= 0 && array[j] > insertNum) {
37 // 元素移动一格
38 array[j + 1] = array[j];
39 // j-- 之后继续于之前的比较，从后往前
40 j--;
41 }
42 // 将需要插入的数放在要插入的位置。
43 array[j + 1] = insertNum;
44 }
45 }
46
47 /**
48 * 希尔排序：
49 * 首先，确定分的组数，然后对组中元素进行插入排序
50 * 接下来，将length/2，重复1,2步，直到length=0 为止。
51 *
52 * @param array
53 */
54 private static void xiErSort(int[] array) {
55 System.out.println("***********希尔排序*************");
56 int length = array.length;
57 while (length != 0) {
58 length = length / 2;
59 // 分的数组
60 for (int x = 0; x < length; x++) {
61 // 组中的元素，从第二个数开始
62 for (int i = x + length; i < array.length; i += length) {
63 // j为有序序列最后一位的位数
64 int j = i - length;
65 // temp 为要插入的元素
66 int temp = array[i];
67 // 从后往前遍历
68 for (; j >= 0 && temp < array[j]; j -= length) {
69 // 向后移动length 位
70 array[j + length] = array[j];
71 }
72 array[j + length] = temp;
73 }
74 }
75 }
76 }
77
78 /**
79 * 简单选择排序：
80 * 首先确定循环次数，并且记住当前数字和当前位置。
81 * 将当前位置后面所有的数与当前数字进行对比，小数赋值给key，并记住小数的位置。
82 * 比对完成后，将最小的值与第一个数的值交换。
83 * 重复2、3步。
84 *
85 * @param array
86 */
87 private static void simpleSelectSort(int[] array) {
88 System.out.println("***********简单选择排序*************");
89 int length = array.length;
90 // 循环次数
91 for (int i = 0; i < length; i++) {
92 int key = array[i];
93 int position = i;
94 // 选出最小的值和位置
95 for (int j = i + 1; j < length; j++) {
96 if (array[j] < key) {
97 key = array[j];
98 position = j;
99 }
100 }
101 // 交换位置
102 array[position] = array[i];
103 array[i] = key;
104 }
105 }
106
107
108 /**
109 * 堆排序：
110 * 将序列构建成大顶堆；
111 * 将根节点与最后一个节点交换，然后断开最后一个节点；
112 * 重复第一、二步，直到所有节点断开。
113 *
114 * @param array
115 */
116 public static void heapSort(int[] array) {
117 System.out.println("***********堆排序*************");
118 System.out.println("开始排序：");
119 int arrayLength = array.length;
120 // 循环建堆
121 for (int i = 0; i < arrayLength - 1; i++) {
122 // 建堆
123 buildMaxHeap(array, arrayLength - 1 - i);
124 // 交换堆顶和最后一个元素
125 swap(array, 0, arrayLength - 1 - i);
126 System.out.println(Arrays.toString(array));
127 }
128 }
129
130 /**
131 * 交换堆顶和最后一个元素
132 *
133 * @param data
134 * @param i
135 * @param j
136 */
137 private static void swap(int[] data, int i, int j) {
138 int tmp = data[i];
139 data[i] = data[j];
140 data[j] = tmp;
141 }
142
143 /**
144 * 建堆：对data数组从0到lastIndex建大顶堆
145 *
146 * @param data
147 * @param lastIndex
148 */
149 private static void buildMaxHeap(int[] data, int lastIndex) {
150 // 从lastIndex处节点（最后一个节点）的父节点开始
151 for (int i = (lastIndex - 1) / 2; i >= 0; i--) {
152 // k保存正在判断的节点
153 int k = i;
154 // 如果当前k节点的子节点存在
155 while (k * 2 + 1 <= lastIndex) {
156 // k节点的左子节点的索引
157 int biggerIndex = 2 * k + 1;
158 //如果biggerIndex小于lastIndex，即biggerIndex+1代表的k节点的右子节点存在
159 if (biggerIndex < lastIndex) {
160 // 若果右子节点的值较大
161 if (data[biggerIndex] < data[biggerIndex + 1]) {
162 // biggerIndex总是记录较大子节点的索引
163 biggerIndex++;
164 }
165 }
166 // 如果k节点的值小于其较大的子节点的值
167 if (data[k] < data[biggerIndex]) {
168 // 交换他们
169 swap(data, k, biggerIndex);
170 // 将biggerIndex赋予k，开始while循环的下一次循环，重新保证k节点的值大于其左右子节点的值
171 k = biggerIndex;
172 } else {
173 break;
174 }
175 }
176 }
177 }
178
179 /**
180 * 冒泡排序：
181 * 设置循环次数。
182 * 设置开始比较的位数，和结束的位数。
183 * 两两比较，将最小的放到前面去。
184 * 重复2、3步，直到循环次数完毕。
185 *
186 * @param array
187 */
188 private static void bubbleSort(int[] array) {
189 int length = array.length;
190 int temp;
191 for (int i = 0; i < length; i++) {
192 for (int j = 0; j < length - i - 1; j++) {
193 if (array[j] > array[j + 1]) {
194 temp = array[j];
195 array[j] = array[j + 1];
196 array[j + 1] = temp;
197 }
198 }
199 }
200 }
201
202 /**
203 * 快速排序：
204 * 选择第一个数为p，小于p的数放在左边，大于p的数放在右边；
205 * 递归的将p左边和右边的数都按照第一步进行，直到不能递归。
206 *
207 * @param array
208 * @param start
209 * @param end
210 */
211 private static void quicklySort(int[] array, int start, int end) {
212 System.out.println("***********快速排序*************");
213 if (start < end) {
214 // 选定的基准值（第一个数值作为基准值）
215 int base = array[start];
216 // 记录临时中间值
217 int temp;
218 int i = start, j = end;
219 do {
220 while ((array[i] < base) && (i < end)) {
221 i++;
222 }
223 while ((array[j] > base) && (j > start)) {
224 j--;
225 }
226 if (i <= j) {
227 temp = array[i];
228 array[i] = array[j];
229 array[j] = temp;
230 i++;
231 j--;
232 }
233 } while (i <= j);
234 if (start < j) {
235 quicklySort(array, start, j);
236 }
237 if (end > i) {
238 quicklySort(array, i, end);
239 }
240 }
241 }
242
243 /**
244 * 归并排序：
245 * 选择相邻两个数组成一个有序序列；
246 * 选择相邻的两个有序序列组成一个有序序列；
247 * 重复第二步，直到全部组成一个有序序列。
248 *
249 * @param arr
250 * @param l
251 * @param r
252 */
253 private static void mergeSort(int[] arr, int l, int r) {
254 System.out.println("***********归并排序*************");
255 if (l < r) {
256 int q = (l + r) / 2;
257 mergeSort(arr, l, q);
258 mergeSort(arr, q + 1, r);
259 merge(arr, l, q, r);
260 }
261 }
262
263 /**
264 * @param arr 排序数组
265 * @param l 数组最左边下标
266 * @param q 数组中间位置下标
267 * @param r 数组最右位置下标
268 */
269 private static void merge(int[] arr, int l, int q, int r) {
270 /**
271 * 因为每次切割后左边下标都是（l,q），右边数组的下标是(q+1,r)
272 * 所以左边数组的元素个数就是q - l + 1
273 * 右边的数组元素个数就是r - q
274 */
275 // 切割后左边数组的数据长度
276 final int n1 = q - l + 1;
277 // 切割后右边数组的数据长度
278 final int n2 = r - q;
279 /**创建两个新数组将切割后的数组分别放进去，长度加1是为了放置无穷大的数据标志位**/
280 // 加一操作是增加无穷大标志位
281 final int[] left = new int[n1 + 1];
282 // 加一操作是增加无穷大标志位
283 final int[] right = new int[n2 + 1];
284 //两个循环将数据添加至新数组中
285 /**左边的数组下标是从l到q**/
286 /**遍历左边的数组*/
287 for (int i = 0; i < n1; i++) {
288 left[i] = arr[l + i];
289 }
290 for (int i = 0; i < n2; i++) {
291 right[i] = arr[q + 1 + i];
292 }
293
294 // 将最大的正整数放在两个新数组的最后一位
295 left[n1] = Integer.MAX_VALUE;
296 right[n2] = Integer.MAX_VALUE;
297
298 int i = 0, j = 0;
299 // 将小的放在前面
300 for (int k = l; k <= r; k++) {
301 if (left[i] <= right[j]) {
302 arr[k] = left[i];
303 i = i + 1;
304 } else {
305 arr[k] = right[j];
306 j = j + 1;
307 }
308 }
309 }
310
311 /**
312 * 基数排序：
313 * 将所有的数的个位数取出，按照个位数进行排序，构成一个序列；
314 * 将新构成的所有的数的十位数取出，按照十位数进行排序，构成一个序列。
315 *
316 * @param array 排序队列中存在负数除外
317 */
318 private static void baseSort(int[] array) {
319 System.out.println("***********基数排序*************");
320 // 首先确定排序的趟数;
321 int max = array[0];
322 for (int i = 1; i < array.length; i++) {
323 if (array[i] > max) {
324 max = array[i];
325 }
326 }
327 int time = 0;
328 // 判断位数;
329 while (max > 0) {
330 max /= 10;
331 time++;
332 }
333 // 建立10个队列;
334 List<ArrayList> queue = new ArrayList<ArrayList>();
335 for (int i = 0; i < 10; i++) {
336 ArrayList<Integer> queue1 = new ArrayList<Integer>();
337 queue.add(queue1);
338 }
339 // 进行time次分配和收集;
340 for (int i = 0; i < time; i++) {
341 //分配数组元素;
342 for (int j = 0; j < array.length; j++) {
343 // 得到数字的第time+1位数;
344 int x = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
345 ArrayList<Integer> queue2 = queue.get(x);
346 queue2.add(array[j]);
347 queue.set(x, queue2);
348 }
349 // 元素计数器;
350 int count = 0;
351 // 收集队列元素;
352 for (int k = 0; k < 10; k++) {
353 while (queue.get(k).size() > 0) {
354 ArrayList<Integer> queue3 = queue.get(k);
355 array[count] = queue3.get(0);
356 queue3.remove(0);
357 count++;
358 }
359 }
360 }
361 }
362
363 /**
364 * 测试排序算法
365 *
366 * @param args
367 */
368 public static void main(String[] args) {
369 int[] array = new int[]{32, 43, 0, 1314, 23, 4, 12, 5, 520};
370 System.out.println("array's origin sort: " + Arrays.toString(array));
371 //justInsertSort(array);
372 //simpleSelectSort(array);
373 //xiErSort(array);
374 //heapSort(array);
375 //bubbleSort(array);
376 //quicklySort(array, 0, array.length - 1);
377 //mergeSort(array, 0, array.length - 1);
378 baseSort(array);
379 System.out.println("array's sort after use algorithm: " + Arrays.toString(array));
380 int[] array2 = new int[]{32, 43, 0, 1314, 23, -4, 12, 5, 520};
381 baseSort(array2);
382
383 }
384
385
386 }
这个世界
需要遗忘的太多
