动态规划---背包
1. 0-1背包问题
有一个容量为V的背包,外面有N件物品。放入第i件物品消耗空间Ci,得到价值Wi,如何装入可使价值总和最大?
每种物品仅有一件
(1)
定义一个N+1行、V+1列的数组arr:arr[i][j]表示前i件物品放到容量为j的背包里面所能获得的最大价值
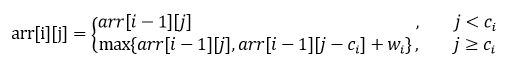
对第i件物品而言,有放或不放两种选择:(1) j<ci ,表示当前空间不够放第i件物品,则当前最大价值就等同于放前 i-1 件物品
(2)当前空间是足以放下第i件物品的:①不放第i件物品,则等同于放前i-1件物品的最大价值
②放第i件物品,则给第i件物品留下足够空间后,剩下空间给前i-1件物品。
假设有5件物品,背包容量10,物品所占空间为:2 5 4 2 3 价值依次为:6 3 5 4 6
依照上面的公式填表:有逗号的地方表示要进行决策,是放当前物品还是不放(前面的更大,表示不放当前物品;后面的更大,表示放当前物品)
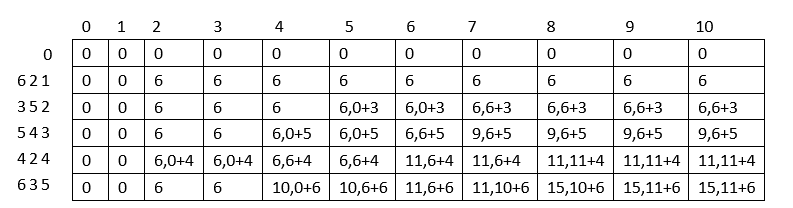
表填完后,最右下角的数arr[N][V]表示N件物品放到容量为V的背包里能获得的最大价值
重构解:两种方式
(1)在做决策时记录,如果放当前物品,则记下其位置
(2)根据arr数组:从最右下角开始,以此为例
arr[5][10] > arr[4][10],说明第5件物品放了,还剩下空间 10-3==7
arr[4][7]==arr[3][7],说明第4件物品没放 还剩下空间7
arr[3][7]>arr[2][7],说明第3件物品放了 还剩下空间 7-4==3
arr[2][3]==arr[1][3] ,说明第2件物品没放 还剩下空间3
arr[1][3]>arr[0][3],说明第1件物品放了 还剩下空间3-2==1
所以放了:第1、第3、第5件物品,且背包还剩下1空间
main.cpp
int c[5] = {2,5,4,2,3}; int w[5] = {6,3,5,4,6}; int maxValue = maxValue_01pack(c,w,5,10);
背包算法部分:
/* c:各物品所占空间 w:各单个物品价值 n:物品数量 V:背包容量 */ int maxValue_01pack(int c[],int w[],int N,int V) { int **arr = getMNMatrix<int>(N+1,V+1); if(nullptr == arr) { return -1; } int maxValue = 0; //arr矩阵填值 for(int i=0;i<=V;i++) { arr[0][i] = 0; } for(int i=0;i<=N;i++) { arr[i][0] = 0; } for(int i=1;i<=N;i++) { for(int j=1;j<=V;j++) {//j代表当前背包容量 if(j<c[i-1]) { arr[i][j] = arr[i-1][j]; } else { arr[i][j] = getMax(arr[i-1][j],arr[i-1][j-c[i-1]]+w[i-1]); } } }
//重构解,由于0-1背包特殊,因此可在arr数组上直接重构解 stack<int> tmp; for(int i=N,j=V;i>0;i--) { if(arr[i][j]>arr[i-1][j]) { tmp.push(i); j -= c[i-1]; } } while(!tmp.empty()) { cout<<tmp.top()<<" "; tmp.pop(); } cout <<endl; maxValue = arr[N][V]; freeMatrix(arr,N+1,V+1); return maxValue; }
2. 完全背包问题
有N种物品,一个容量为V的背包,每种物品有无限件可用。
放入第i种物品占ci,价值wi
分析:
每种物品可选0件、1件..... [V/ci]件
用arr[i][j]表示前i种物品放入容量为j的背包时的最大权值,则有方程:
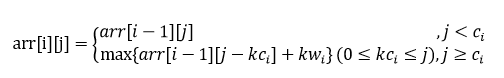
0-1背包的递推式与此不同的是,k只取0和1
类似0-1背包填表,但对每一个位置时间不是常数级别,而是O(j/ci),则总的时间复杂度为O(N*V*ΣV/ci)
填完表后,最右下角的数就是最大值,关键在于如何重构解:用一个N行V列数组存储第i件物品在当前体积下所取的k值,即是第i件物品的个数(0-1背包由于k只取0或1的原因,可直接通过arr数组推导各物品的个数,因此不用
再建立一个N*V的求解数组了)
例子:5件物品,背包体积10,各物品占体积如下c,价值如w
int c[5] = {2,5,4,2,3}; int w[5] = {6,3,5,4,10}; int maxValue = maxValue_pack(c,w,5,10);
具体的求解及重构解的函数如下:
int maxValue_pack(int c[],int w[],int N,int V) { vector<vector<int>> d(N+1,vector<int>(V+1,0));//N+1行 V+1列 vector<vector<int>> num(N,vector<int>(V,0));//用于重构解 int i,j,k; int num_i = 0;//第i件物品在各种v的情况下的个数,i从1开始 for( i=1;i<=N;i++) { num_i = 0; for( j=1;j<=V;j++) { for( k=0;k*c[i-1]<=j;k++) { if(d[i][j]<d[i-1][j-k*c[i-1]]+k*w[i-1]) { d[i][j] = d[i-1][j-k*c[i-1]]+k*w[i-1]; num_i = k; } } num[i-1][j-1] = num_i; } } //重构解 stack<pair<int,int>> solution; for(int i=N,j=V;(i>=0)&&(j>0);i--) { //j>0条件是必要的,比如全部选择最后一个物品,空间也用完了,再去找前面的物品时,会有 num[i-1][0-1]越界错误 if(num[i-1][j-1] != 0) { solution.push({i,num[i-1][j-1]}); j -= (num[i-1][j-1]*c[i-1]); } } while(!solution.empty()) { cout<<solution.top().first<<"号:"<<solution.top().second<<"个"<<endl; solution.pop(); } return d[N][V]; }
调试输出:
d数组内容如下:

num数组的内容如下:

3. 多重背包问题
4. 混合三种背包问题
5.二维费用的背包问题
6. 分组的背包问题
问题:
N件物品,容量为V的背包
第i件物品费用ci,价值wi
物品划分为K组,每组中物品相互冲突,最多选一件
求解:价值总和=物品数量*物品价值,累加
分析:
完全背包问题是每件物品有若干选择策略,而分组背包是每组物品有若干策略(是选择本组的一件,或者本组一件都不选)
F[k,v]表示前k组物品花费空间v所能取得的最大权值
F[k,v] = max{F[k-1,v],F[k-1,v-ci]+wi | i∈组k}
对比于0-1背包,里面的一个物品,在这里是一组物品
实现:
一个 K*V 的d数组,存储最大权值计算结果;一个 K*V 的so数组,存储各组在当前容量下物品的下标,如果当前组不选,则该值为-1
/* a:各物品属性信息 N:物品数量 V:背包容量 K:分组数 num:各组物品件数,例题中为 0 2 3 2 */ int maxValue_array_pack(vector<goods> &a,int N,int V,int K,int num[]) { //2个K*V的二维数组,一个为求解用, 一个用来重构解 vector<vector<int>> d(K+1,vector<int>(V+1,0)); vector<vector<int>> so(K,vector<int>(V,-1)); int i_in_k = 0; int i_index = 0; for(int k=1;k<=K;k++) { for(int v=1;v<=V;v++) { i_in_k = -1;//表示当前组不选,如果选一个,则此变量值为该物品在a数组中的下标 d[k][v] = d[k-1][v]; for(int i = i_index;i<i_index+num[k];i++) { //遍历第k组里面的所有物品 if(v>=a[i].c) { if (d[k][v] < d[k - 1][v - a[i].c] + a[i].w) { d[k][v] = d[k - 1][v - a[i].c] + a[i].w; i_in_k = i; } } } so[k-1][v-1] = i_in_k; //当前组在各种容量下的解决方案出来了 } i_index += num[k]; } cout<<"最大权值:"<<d[K][V]<<endl; //重构解 stack<int> solution; for(int i=K,j=V;(i>=0)&&(j>0);i--) { if(so[i-1][j-1] != -1) { solution.push(so[i-1][j-1]); j -= (a[so[i-1][j-1]].c); } } ostringstream cost; ostringstream value; while(!solution.empty()) { cout<<"第"<<solution.top()+1<<"件物品"<<endl; if(solution.size()==1) { cost<<a[solution.top()].c; value<<a[solution.top()].w; } else { cost<<a[solution.top()].c<<"+"; value<<a[solution.top()].w<<"+"; } solution.pop(); } cout<<"空间消耗:"<<cost.str()<<endl; cout<<"权值组成:"<<value.str()<<endl; return d[K][V]; }
调用上面函数的入参和初始化:
typedef struct goods { int c; //消耗 int w;//收益、价值、重要度等 int flag;//区分组、主附件等 }goods; vector<goods> a; int N,V; initGoods(a,N,V); int num[4] = {0,2,3,2}; //第1分组有2个物品,第2分组有3个物品,第3分组有2个物品 maxValue_array_pack(a,N,V,3,num); //这个分组数为3,暂时写死,包括上面的num数组都可以通过goods数组里的数据统计而来,暂时不管了
void initGoods(vector<goods> &a,int &N,int &V) { cout<<"输入物品总数量N:";cin>>N; cout<<"输入背包容量V:"; cin>>V; for(int i=0;i<N;i++) { goods x; cout<<"输入第"<<i+1<<"件物品的消耗c:";cin>>x.c; cout<<"输入第"<<i+1<<"件物品的价值w:";cin>>x.w; cout<<"输入第"<<i+1<<"件物品的标志flag:";cin>>x.flag; a.push_back(x); } cout<<"信息录入完成."<<endl; }
调试用物品信息:
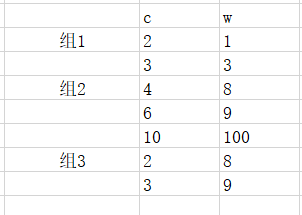
d数组数据:

so数组数据:

7. 有依赖的背包问题
物品间存在依赖关系,物品a依赖于物品b,如果要选物品a的话,则必须先选b(b为主件,a为主件a的附件)
现有多个物品,其中有主件也有附件,一个主件会有多个附件,但只能选择0个附件、1个附件、2个附件....等这些方案中的一个。
对于某一个主件,可用策略如:此主件不选、仅有主件、主件加1个附件、主件加2个附件....【每件物品只选一个,不是完全背包的选无限个,如1主件只能买1个、1号附件只能买1个...】
由于主件和附件选择互斥,所以可将每一种策略视作一个组,在这个组内选一个方案【这个组内方案是很多的,设主件A有n个可选附件,则方案有:
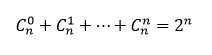 再加上不选主件的情况,有2n+1种可行方案】
再加上不选主件的情况,有2n+1种可行方案】
例题:金明的预算方案
有V元钱,N件物品,第i件物品价格/消耗为ci,重要度/价值为wi 。每个主件最多2个附件。每件物品最多买一件。
目标:价格*重要度的累加和最大
输入:V钱数;N物品数;各物品价格 、重要度、主还是附件
---------------------------------------------------------------------------------------------------------------------------
8. 要求背包全部用完和不要求全部用完的区别
9. 时间复杂度的优化
10. 空间复杂度的优化


