动态规划
动态规划与分治：
都是将较大规模的问题分解成子问题求解
分治：问题分解-----递归求解子问题--------子问题解组合求得原问题的解
动态规划：分治划分的子问题，会重复计算相同规模的子问题，即会有重叠的子问题求解，因此当规模很大时，效率变低
动态规划用来处理子问题重叠的情况，将子问题求解保存，再遇到相同规模的子问题时，不再求解，避免了很多重复工作
动态规划相关概念：
要使用动态规划解决问题，则该问题必须要有最优子结构性质 ，且
（1）最优子结构
①一个问题的最优解包含其子问题的最优解，则此问题有 最优子结构 性质
②对于不同的问题，最优子结构的不同体现在：
原问题的最优解中涉及多少个子问题
在确定最优解使用哪些子问题时，需要考察多少种选择
（2）子问题重叠
递归算法反复求解相同的子问题
动态规划问题，一般使用自底向上的最优子结构：首先求子问题最优解，在子问题最优解基础上求原问题最优解
贪心：并不首先寻找子问题最优解，而是先做出一个"贪心"选择，即当时/局部最优选择，然后求解选出的子问题（而不像动态规划去求解所有相关的子问题）
-----------------------------------------------------------------------------------------------------------------------------------------------------------
1. 钢条切割问题
出售一段长度为i的钢条的价格为pi
| 长度 i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 价格 pi | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
现在给定一个长度为 n 的钢条，如何切割可使收益 rn 最大（这个很像背包问题，背包容量为n，物品占空间为i，且各个物品无限多）
（1）有多少种切割方案
假设有一段长为4的钢条如下图
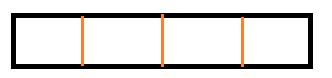
橙色为可以切割的点，则有多少种切割方案成了组合问题：切0次、切1次、切2次、切3次
共：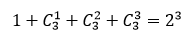
中方案（里面有相同的方案，比如分成1+1+2 和 1+2+1），如果要计算不重复的方案，要用 划分函数
则长度为n的有 2n-1 种方案
（2）模型1
n=1，r1 = p1
n=2，r2=max(p2,r1+r1)
n=3，r3=max(p3,r1+r2,r2+r1)
n=4，r4=max(p4,r1+r3,r2+r2,r3+r1)
....
长度为n，rn=max(pn,r1+rn-1,r2+rn-2,...rn-1+r1) 其实pn就相当于rn+r0 ,此公式也可写为 rn=max(r1+rn-1,....rn+r0)
为求解规模为n的原问题，需要求解形式一样，但规模小一些的子问题。最终问题的解由各子问题的解组合起来，而各个子问题也可以独立求解。
（3）模型2 这个模型2还有点不太理解
上面的模型1将一个问题分解成两个子问题，再对两个子问题继续分解求解。
将长度为n的钢条切下长度为i的一段，这块长度为i的不再切割，只对剩下长度为n-i的继续切割（递归求解）。则可得到公式如下：
rn=max(p1+rn-1,p2+rn-2.....pn+r0)
按照模型2，一个问题只需要计算一个子问题的解
下面按照模型2进行分析：
（4）自顶向下的递归求解----------这实际上是分治的做法
伪代码：
CUT-ROD(p,n) if n==0 return 0 q = -无穷 for i = 1 to n q = max(q,p[i]+CUT-ROD(p,n-i)) return q
当n=4时，调用过程如下：每个结点表示调用 CUT-ROD函数
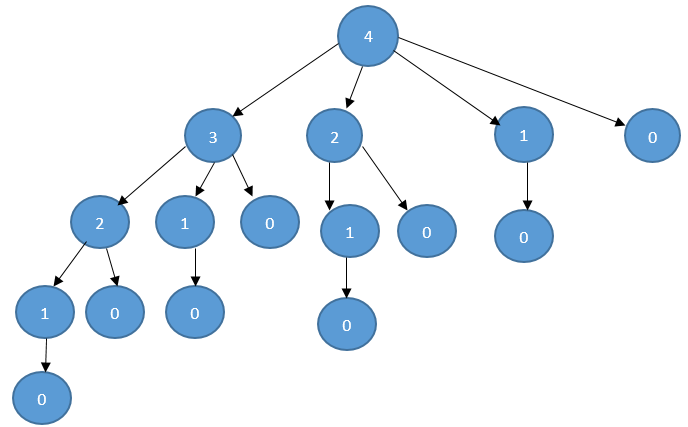
对于长度为n的，CUT-ROD的调用次数为 2n
效率低，以上面图为例，要求解n为3的问题，需要求解n为2和n为1的子问题，在n为2的子问题里面又求解n为1的子问题，这里就出现了重复计算，从整个图来看，有很多的重复计算。
-------------------------------------------------------------------------
简单实现：C++
dynamicProgram.h
#ifndef TESTCPLUS_DYNAMICPROGRAM_H #define TESTCPLUS_DYNAMICPROGRAM_H int cut_rod(int p[],int n); extern int pi[22]; extern int cutCount; #endif
dynamicOrogram.cpp
#include <iostream> #include "dynamicProgram.h" using namespace std; //1.钢条切割 int pi[22] = {0,1,5,8,9,10,17,17,20,24,30,31,32,33,34,35,36,37,38,39,40,41};//长度为i的钢条价值 int cutCount = 0; static int getMax(int a,int b) { return a>b?a:b; } int cut_rod(int p[],int n) { ++cutCount; if(n == 0) { //递归出口 return 0; } int tmp = -1; for(int i=1;i<=n;i++) { tmp = getMax(tmp,p[i]+cut_rod(p,n-i)); } return tmp; }
main.cpp
#include <iostream> #include "dynamicProgram.h" using namespace std; int main(int argc, char** argv) { for(int i=1;i<=21;i++) { int maxValue = cut_rod(pi,i); cout<<"length "<<i<<":maxValue="<<maxValue<<" cutCount= "<<cutCount<<endl; cutCount = 0; } return 0; }
计算结果：获得长度为1~21时，最大收益maxValue，以及调用cut_rod函数的次数
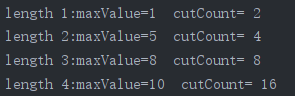
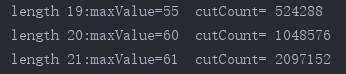
可见，调用次数与问题规模n成指数性增长
（5）动态规划求解
自顶向下的递归求解效率低的原因在于重复计算了相同的子问题，动态规划通过合理安排求解顺序，对每个相同规模的子问题只求解一次，保存该规模的子问题解，在后面如果又要求解同等规模的子问题，则不需要再次计算，而直接从之前保存的结果里面取值。
①带备忘的自顶向下求解
类似（3）里面用递归方式计算，但将各子问题的解保存在数组或散列表中，后面需要求解一个子问题时，先检查是否已经保存了这个规模问题的解，如果已经有了则直接返回保存的该值，否则就要计算。
伪代码：
CUT-ROD-MEM(p,n) r[n+1] = 0,-无穷,-无穷.... return CUT-ROD-MEM-(p,n,r) CUT-ROD-MEM-(p,n,r) if r[n]>=0 return r[n] if n == 0 return 0 q = -无穷 for i = 1 to n q = max(q,p[i]+CUT-ROD-MEM-(p,n-i,r)) r[n] = q return q
实现：
int cut_rod_mem(int p[],int n) { int *r = (int *)malloc((n+1)*sizeof(int)); if(NULL == r) { return -1; } r[0] = 0; for(int i=1;i<=n;i++) { r[i] = -1; } int res = cut_rod_mem_(p,n,r); free(r); return res; } int cut_rod_mem_(int p[],int n,int r[]) { ++cutCount; if(r[n] >= 0) { return r[n]; } if(n == 0) { return 0; } int tmp = -1; for(int i=1;i<=n;i++) { tmp = getMax(tmp,p[i]+cut_rod_mem_(p,n-i,r)); } r[n] = tmp; return tmp; }
用(4)的main去测试：查看调用cut_rod_mem_的次数
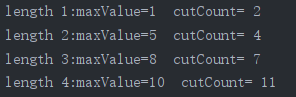
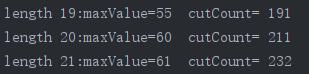
当n较小时，差别不大；但当n变大后，调用次数出现很明显的差别（比如n为21时，不带备忘的递归调用了2097152次，而带备忘的调用了232次）
②自底向上的版本
先计算出n为1的最大收益并保存；计算n为2时最大收益：从p1+r1 和p2 +r0中取出最大值作为r2 ...
n为3时，则从 p1+r2 p2+r1 p3 中取最大值.....
由于先计算n较小时的最大收益，后面计算较大的n时，基于已经求得的较小的n的最大收益进行计算
伪代码：
BOTTOM-UP_CUT-ROD(p,n) r[n+1] r[0]=0 for i = 1 to n q = -无穷 for j = 1 to i q = max(q,p[j]+r[i-j]) r[i] = q return r[n]
实现：
int bottom_up_cut_rod(int p[],int n) { int *r = (int *)malloc((n+1)*sizeof(int)); if(NULL == r) { return -1; } r[0] = 0; for(int i=1;i<=n;i++) { int tmp = -1; for(int j=1;j<=i;j++) {
++cutCount; tmp = getMax(tmp,p[j]+r[i-j]); } r[i] = tmp; } int res = r[n]; free(r); return res; }
用（4）的main测试：
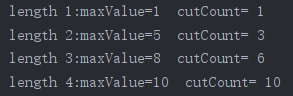
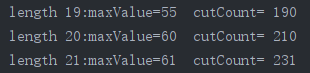
自底向上的特点：
for执行次数是以1为公差等差数列的前n项和 次 O(n2) ,上面的带备忘的递归也是O(n2)
（6）完全的解
上面不管是分治还是动态规划都只计算出了最大收益，没有输出实际的方案
①带备忘的自顶向下的递归
②自底向上的方法
伪代码：
EXTENDED-BOTTOM-UP_CUT-ROD(p,n) r[n+1] s[n+1] r[0] = 0 for i = 1 to n q = -无穷 for j = 1 to i if q<p[j]+r[i-j] q = p[j]+r[i-j] s[i] = j r[i] = q return r s
s[i]的值：长度为i的切出来第一部分（这部分不再切割）的长度，剩下 i - s[i] 怎么切割呢：s[ i - s[i] ] 递推即可
输出切割方案的伪代码：
PRINT(p,n) r,s = EXTENDED-BOTTOM-UP-CUT-ROD(p,n) while n>0 print s[n] n = n-s[n]
C++实现：
int extended_bottom_up_cut_rod(int p[],int n,int s[]) { int *r = (int *)malloc((n+1)*sizeof(int)); if(NULL == r) { return -1; } r[0] = 0; s[0] = 0; for(int i=1;i<=n;i++) { int tmp = -1; for(int j=1;j<=i;j++) { if(tmp<p[j]+r[i-j]) { tmp = p[j] + r[i-j]; s[i] = j; } } r[i] = tmp; } int res = r[n]; free(r); return res; }
调用：
int value4[22] = {0}; int s[22] = {0}; for(int i=0;i<=21;i++) { int maxValue = extended_bottom_up_cut_rod(pi,i,s); value4[i] = maxValue; } for(int i=1;i<22;i++) { cout<<"length "<<i<<":maxValue="<<value4[i]<<" solution:"; int j = i; while(j>0) { if((j-s[j])<=0) { cout<<s[j]; } else { cout<<s[j]<<"+"; } j = j - s[j]; } cout<<endl; }
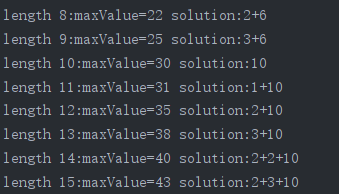
2. 矩阵链乘
3. 最长不下降子序列
给定一个乱序整型数组，求最长不下降子序列、最长上升子序列，并输出序列（如果有多个可行的序列呢）
upper_bound：返回给定区间[first,last)中第一个比给定参数大的元素的迭代器
lower_bound：返回给定区间[first,last)中第一个比给定参数大或相等的元素的迭代器
（1）最长不下降
从前往后遍历原序列：
来第一个数字，则认为其是当前最长序列，长度为1
来第二个数字：①比前一个大或相等(不下降，则可以相等)，则可以接在前面的数字后面，最长序列长度加1
②比前一个小，则在已经确定的最长序列里面往前找，找到第一个大于它的数，并替换它（为什么要用这个数替换？因为它比那找到的第一个大于它的数更有前途）
例：已知前面的是1,2,3,5 下一个数字是4，我们不知道后面还有哪些数字，但4肯定比5更有前途使序列变得更长
后面的步骤是一样的
首先，需要一个跟原序列同样长度的数组d保存相关元素：d[i]表示长度为i的不下降序列的最小的末尾元素
例：原序列1,2,3,4,8,9,5,6 则根据规则①和②最后d数组的保存结果为：1,2,3,4,5,6
输出最长序列：
在遍历原序列时，标记该元素在最长序列中的位置。比如上面的1,2,3,4,8,9,5,6，用一个数组mark依次标记为1,2,3,4,5,6,5,6，当然数组下标从0开始，所以依次还要小1
找完最长子序列后，从原序列最后往前找：先找mark[i]为len的，再找mark[i]为len-1的，直到找完
int longerNDSubseqRes(int src[],int n,int res[]) { if(NULL == src || n == 0 || NULL == res) { return 0; } int *d = (int *)malloc(n*sizeof(int)); if(NULL == d) { return 0; } int *mark = (int *)malloc(n*sizeof(int)); if(NULL == mark) { free(d); return 0; } d[0] = src[0]; mark[0] = 0; int len = 0; for(int i=1;i<n;i++) { if(src[i]>=d[len]) { d[++len] = src[i]; mark[i] = len; } else { int firstBiger = upper_bound(d,d+len+1,src[i])-d; d[firstBiger] = src[i]; mark[i] = firstBiger; } } //输出序列 stack<int> tmp; for(int i=n-1,j=len;i>=0;i--) { if(mark[i] == j) { tmp.push(src[i]); --j; } if(j<0) { break; } } int i = 0; while(!tmp.empty()) { res[i++] = tmp.top(); tmp.pop(); } free(d); free(mark); return len+1; }
（2）最长上升
对于要求序列严格递增，与（1）的不下降序列比较，有几个地方不同
①如果数字比前一个大（而不是大于等于）则，这个数字可以加入到最长序列中，序列长度加1
②如果数字与前一个相等，则忽略
③如果数字比前一个小，则在已确定的最长序列里面往前找，找到第一个大于等于（而不是大于）它的数，并替换之
int longerNDSubseqRes(int src[],int n,int res[]) { if(NULL == src || n == 0 || NULL == res) { return 0; } int *d = (int *)malloc(n*sizeof(int)); if(NULL == d) { return 0; } int *mark = (int *)malloc(n*sizeof(int)); if(NULL == mark) { free(d); return 0; } d[0] = src[0]; mark[0] = 0; int len = 0; for(int i=1;i<n;i++) { if(src[i]>d[len]) { //改动1 d[++len] = src[i]; mark[i] = len; } else { int firstBiger = lower_bound(d,d+len+1,src[i])-d; //改动2 d[firstBiger] = src[i]; mark[i] = firstBiger; } } //输出序列 stack<int> tmp; for(int i=n-1,j=len;i>=0;i--) { if(mark[i] == j) { tmp.push(src[i]); --j; } if(j<0) { break; } } int i = 0; while(!tmp.empty()) { res[i++] = tmp.top(); tmp.pop(); } free(d); free(mark); return len+1; }
4. 最长公共子序列
前缀：序列X=<A,B,C,D,E,F> X0为空；第1前缀为X1 =<A> ；第2前缀为 X2=<A,B> .....
LCS最优子结构：X=<x1,x2,x3,...xm> Y=<y1,y2,y3,...yn> Z=<z1,z2....zk>为X和Y的任一LCS
①如果xm==yn，则zk==xm==yn，且Zk-1是Xm-1和Yn-1的一个LCS
②如果xm != yn：
如果zk != xm，则Z是Xm-1和Y的一个LCS
如果zk != yn，则Z是X和Yn-1的一个LCS
两序列的LCS包含该序列小一点规模序列的LCS
定义 c[i,j] 为Xi和Yj的LCS长度，则有公式：
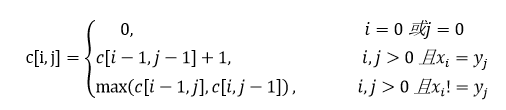
对于m个元素的序列x、n个元素的序列y，需要(m+1)*(n+1)的辅助空间来计算长度：行0、列0都为0，最大长度的值就是c[m][n]
构建出来的c数组如图：
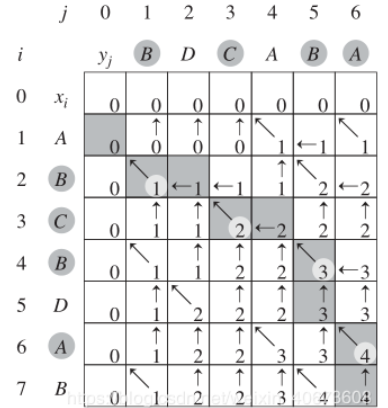
如何重构共同序列：增加一个m*n的b数组，在构建c数组的时候，对于上面的三种情况（xi==yj、xi!=yj、xi!=yj三种）分别做标记，也就是上面图里面的箭头。数组构建完成后，从最后往前找，找到一个指向左上的箭头，则此位置对应的就是xi==yj的情况，此字符就是公共序列中的一个。
int longestCommonSeq(char x[],int m,char y[],int n,char res[]) { //...参数检测 char **c = getMNMatrix<char>(m+1,n+1); if(nullptr == c) { return 0; } char **b = getMNMatrix<char>(m,n); if(nullptr == b) { freeMatrix(c,m+1,n+1); return 0; } for(int i=0;i<m+1;i++) { c[i][0] = 0; } for(int j=0;j<n+1;j++) { c[0][j] = 0; } for(int i=0;i<m;i++) { for(int j=0;j<n;j++) { if(x[i] == y[j]) { c[i+1][j+1] = c[i][j] + 1; b[i][j] = '1';//左上 } else if(c[i][j+1]>=c[i+1][j]) { c[i+1][j+1] = c[i][j+1]; b[i][j] = '2';//上 } else { c[i+1][j+1] = c[i+1][j]; b[i][j] = '3'; //左 } } } int maxLen = c[m][n]; //构建最长公共序列 通过数组b int bi = m-1,bj = n-1; stack<char> tmp; while((bi >= 0) && (bj >= 0)) { if(b[bi][bj] == '1') { tmp.push(x[bi]);//或者y[bj] bi--; bj--; } else if(b[bi][bj] == '2') { bi--; } else { bj--; } } bi = 0; while(!tmp.empty()) { res[bi++] = tmp.top(); tmp.pop(); } freeMatrix(c,m+1,n+1); freeMatrix(b,m,n); return maxLen; }
时间：O(m*n)
空间：O(m*n*2)
优化：时间和空间都还可以优化..................
5. 最长公共子串
与公共子序列相似，但要求更严格，要求公共部分是连续的
如果两个字符不等，则c数组对应位置为0；如果相等，则对应位置的值为其左上角值加1
假设两个串为："acbcbcef"、"abcbced" ，构建c数组如下
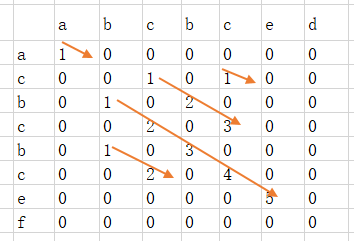
c数组里面最大值即为最长公共子串长度；重构公共子串就从该位置往左上方找，直到找到值为1为止。
int longestCommonStr(char x[],int m,char y[],int n,char res[]) { //...参数检测，包括m、n为0的情况暂时排除 char **c = getMNMatrix<char>(m,n); if(nullptr == c) { return 0; } int maxIndex = 0; int maxLen = 0; for(int i=0;i<m;i++) { for(int j=0;j<n;j++) { if(x[i] == y[j]) { if(i==0 || j==0) { c[i][j] = 1; } else { c[i][j] = c[i-1][j-1] + 1; } if(c[i][j] > maxLen) { maxLen = c[i][j]; maxIndex = i; } } else { c[i][j] = 0; } } } for(int i=maxIndex-maxLen+1,j=0;i<=maxIndex;i++) { res[j++] = x[i]; } freeMatrix(c,m,n); return maxLen; }
6. 背包
7. 最优二叉搜索树
