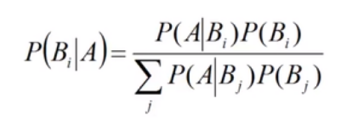2.机器学习相关数学基础
1)贴上视频学习笔记,要求真实,不要抄袭,可以手写拍照。















2)用自己的话总结“梯度”,“梯度下降”和“贝叶斯定理”,可以word编辑,可做思维导图,可以手写拍照,要求言简意赅、排版整洁。
“梯度”:是一个向量;每个元素为函数对一元变量的偏导数;它既有大小(其大小为最大方向导数),也有方向。沿着梯度向量的方向,更加容易找到函数的最大值。反过来说,沿着梯度向量相反的方向,梯度减少最快,也就是更加容易找到函数的最小值。
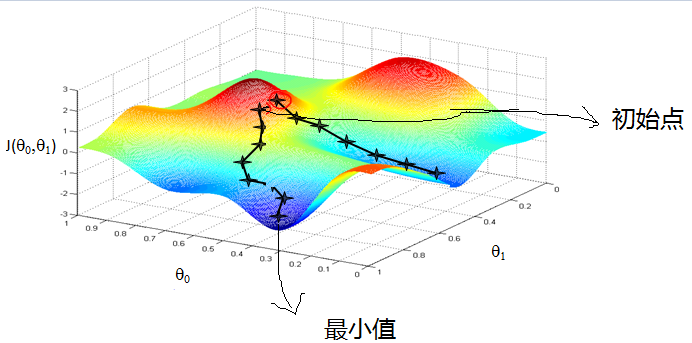
“梯度下降”:比如我们在一座大山上的某处位置,由于我们不知道怎么下山,于是决定走一步算一步,也就是在每走到一个位置的时候,求解当前位置的梯度,沿着梯度的负方向,也就是当前最陡峭的位置向下走一步,然后继续求解当前位置梯度,向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去,一直走到觉得我们已经到了山脚。当然这样走下去,有可能我们不能走到山脚,而是到了某一个局部的山峰低处。梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。
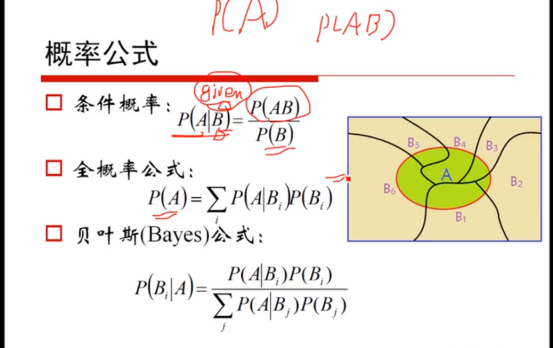
“贝叶斯定理”:其实这个的定理就是当你求 A条件下B1的概率 时,通过相反方面来求,用 B1条件下A的概率 除以 所有B条件下A的概率,即 :