【数据结构】 顺序表查找（折半查找&&差值查找）

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAXSIZE 10

首先构造一个数组， 由随机数生成， 同时确保没有重复元素。（为了排序之后查找时候方便）

为了确保没有重复的元素使用了一个简单的查找函数：

用数组的0号元素来作为哨兵

化简了操作：

int search0(int *a,int length,int key)
{
    int i;
    a[0] = key;
    i = length;
    while(a[i]!=key)
    {
        i--;
    }
    return i;  //这样如果没有查找到元素，就会return 0；
}

 

int a[MAXSIZE] = {0};
    int i;
    int find;
    int rec;
    srand((unsigned)time(NULL));
    for(i=1;i<MAXSIZE+1;i++)
    {
        a[i] = rand()%20+1;
        while(search0(a,i-1,a[i])!=0&&i!=1&&i!=MAXSIZE+1)
            a[i]=rand()%10+1;
    }

还需要一个函数 显示数组里所有元素：

void print_List(int *a,int length)
{
    int i;
    printf("List:");
    for(i=1;i<length+1;i++)
    {
        printf(" %d ",a[i]);
    }
    printf("\n");
}

使用冒泡法进行排序：

void sort(int *a,int length)
{
    int i,j;
    int t;
    for(i=1;i<length+1;i++)
    {
        for(j=i+1;j<length+1;j++)
        {
            if(a[i]>a[j])
            {
                t = a[i];
                a[i] = a[j];
                a[j] = t;
            }
        }
    }
}

之后是折半查找的函数：

int search_half(int *a,int length,int key)
{
    int low,high,mid;
    low = 1;
    high = length;
    int n = 1;
    while(low<=high)
    {
        //mid = (low + high)/2;                                              //折半查找
        mid = low+ (high - low)*(key-a[low])/(a[high]-a[low]);               //差值查找
        printf("%d: low = %d high = %d mid = %d\n",n,low,high,mid);
        if(key<a[mid])
            high= mid - 1;
        else if (key>a[mid])
            low = mid + 1;
        else
            return mid;
        n++;
    }
    return 0;
}

首先需要确保是一个有序的表，这样通过比较key 和 mid的大小

如果key小于mid则说明key可能在小于mid的区域 high 调整

如果key大于mid则说明key可能在大于mid的区域 low 调整

相等就找到了

效果如图：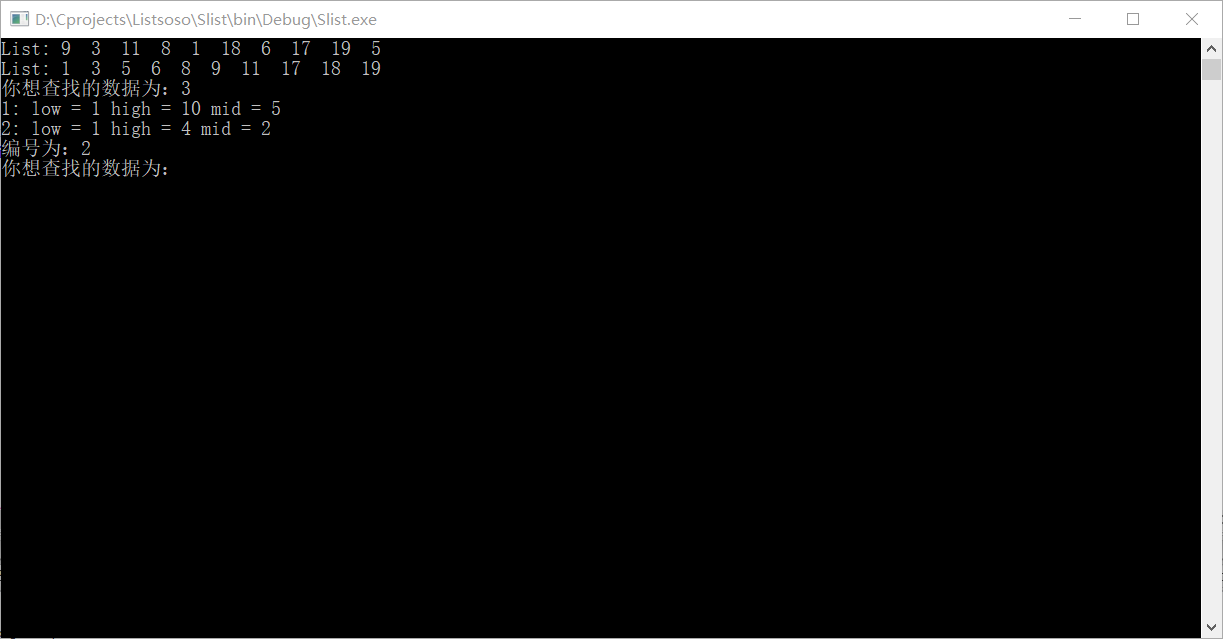

那么另一个问题出现了：为什么一定要折半呢？

 比如说在0~1000内查找5 折半就很不明智了吧。

最初的公式可以理解为：

　　mid = (low+high)/2 = low+1/2*(high - low)

　　即 在low这个基础数值上附加了一个数值 （这里是选择区间数值的一半）， 如果我们想改进这个公式， 显然应该改进那个附加值 改为与key 相关

       mid = low+(key-a[low])/(a[high]-a[low])*(highj - low)

比如说还是在 0~1000个内寻找5

第一次的mid 修改为 mid = 0+（5-0）/（1000-0）*1000 = 5   显然能看出 当插值明显很小（或者很大） mid 的取值取决于key在整体的大小趋势， 这样mid也会明显变小（或者很大）

测试， 将MAXSIZE 增大为20

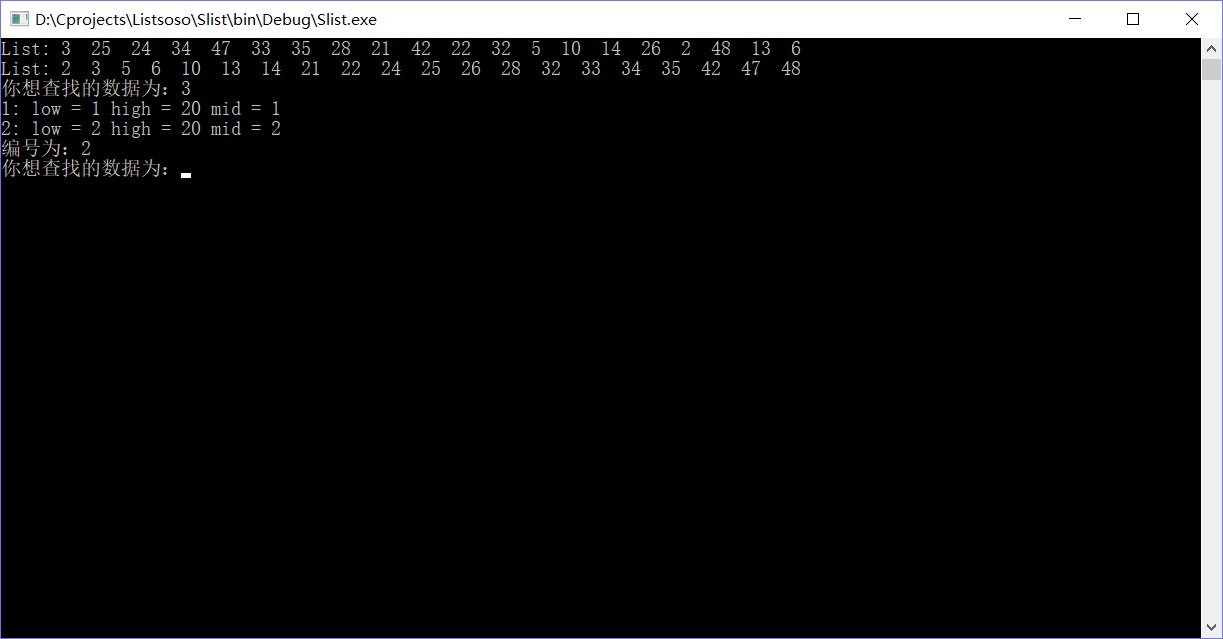
比常规的折半相比， 速度更快了。

完整程序：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAXSIZE 20
void print_List(int *a,int length)
{
    int i;
    printf("List:");
    for(i=1;i<length+1;i++)
    {
        printf(" %d ",a[i]);
    }
    printf("\n");
}

void sort(int *a,int length)
{
    int i,j;
    int t;
    for(i=1;i<length+1;i++)
    {
        for(j=i+1;j<length+1;j++)
        {
            if(a[i]>a[j])
            {
                t = a[i];
                a[i] = a[j];
                a[j] = t;
            }
        }
    }
}
int search0(int *a,int length,int key)
{
    int i;
    a[0] = key;
    i = length;
    while(a[i]!=key)
    {
        i--;
    }
    return i;
}
int search_half(int *a,int length,int key)
{
    int low,high,mid;
    low = 1;
    high = length;
    int n = 1;
    while(low<=high)
    {
        //mid = (low + high)/2;                                              //折半查找
        mid = low+ (high - low)*(key-a[low])/(a[high]-a[low]);               //差值查找
        printf("%d: low = %d high = %d mid = %d\n",n,low,high,mid);
        if(key<a[mid])
            high= mid - 1;
        else if (key>a[mid])
            low = mid + 1;
        else
            return mid;
        n++;
    }
    return 0;
}
int main()
{
    int a[MAXSIZE] = {0};
    int i;
    int find;
    int rec;
    srand((unsigned)time(NULL));
    for(i=1;i<MAXSIZE+1;i++)
    {
        a[i] = rand()%50+1;
        while(search0(a,i-1,a[i])!=0&&i!=1&&i!=MAXSIZE+1)
            a[i]=rand()%10+1;
    }
    print_List(a,MAXSIZE);
    sort(a,MAXSIZE);
    print_List(a,MAXSIZE);
    while(1)
    {
        printf("你想查找的数据为：");
        scanf("%d",&find);
        rec=search_half(a,MAXSIZE,find);
        if(rec != 0)
            printf("编号为：%d\n",rec);
        else
            printf("没找到\n");
    }
    return 0;
}