回溯算法

1.八皇后问题

在n*n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规矩，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n后问题等价于在n*n格的棋盘上方置n个皇后，任何2个皇后不放在同一行或同一列或同一斜线上。我们需要求的是可放置的总数。

 

 

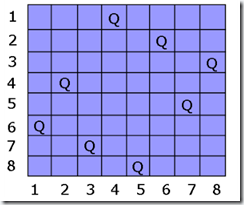
基本思路:  用一个数组X[1]到X[n]来表示问题的解,  其中X[i]代表第i个皇后放在第 i 行 X[i] 列, 因为不能在同一列, 所以X[i]都不相同.  假设两个皇后分别在第 i 和 j 行, 对于任意两个皇后不能放在同一斜线上这个条件, 我们可以转化为 | i - j| != | X[i] - X[j] |,  因为依照上图建立坐标系,   如果 i - X[i] = j - X[j] 或者 i + X[i] = j + X[j], 则两个坐标斜率相等, 两个皇后必然在同一斜线上.  

 

参考代码

 

public class EightQueens {
    private static int N = 10;    //8皇后
    private static int[] X = new int[N + 1];    //每个皇后的位置
    private static int sum = 0;    //解法个数
    
    /*检查当前位置是否冲突*/
    public static boolean check(int n){
        for(int i = 1; i < n; i++)
            if(Math.abs(n - i) == Math.abs(X[n] - X[i]) || X[n] == X[i]) return false;
        return true;
    }
    
    /*t表示当前行数*/
    public static void backtrak(int t){
        if(t > N) sum++;
        else{
            for(int i = 1; i <= N; i++){
                X[t] = i;
                if(check(t)) backtrak(t+1);
            }
        }
    }
    
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        for(int i = 0; i <= N; i++){
            X[i] = 0;
        }
        backtrak(1);
        System.out.println(sum);
    }

}