《机器学习》第二次作业——第四章学习记录和心得
思维导图
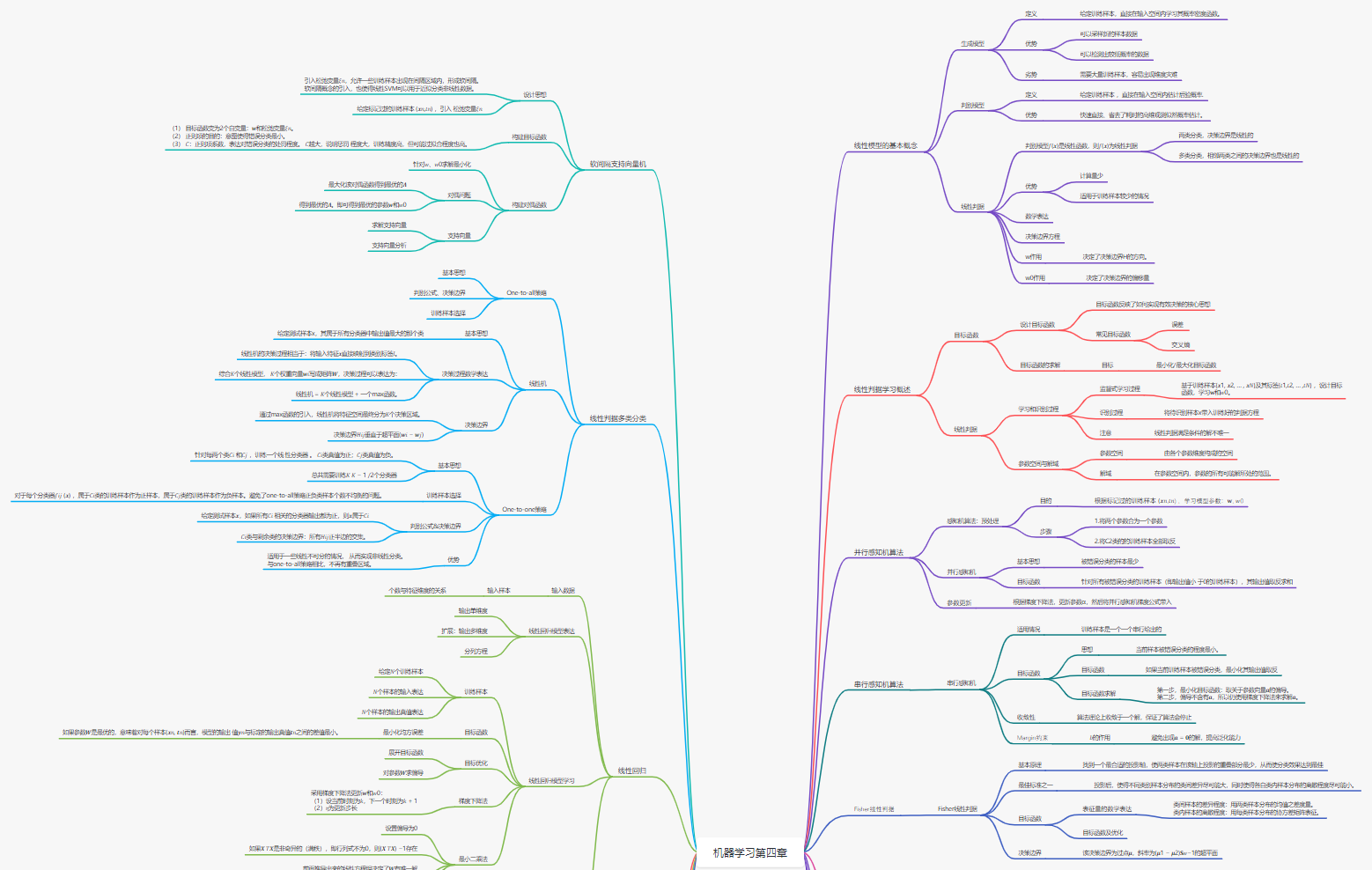
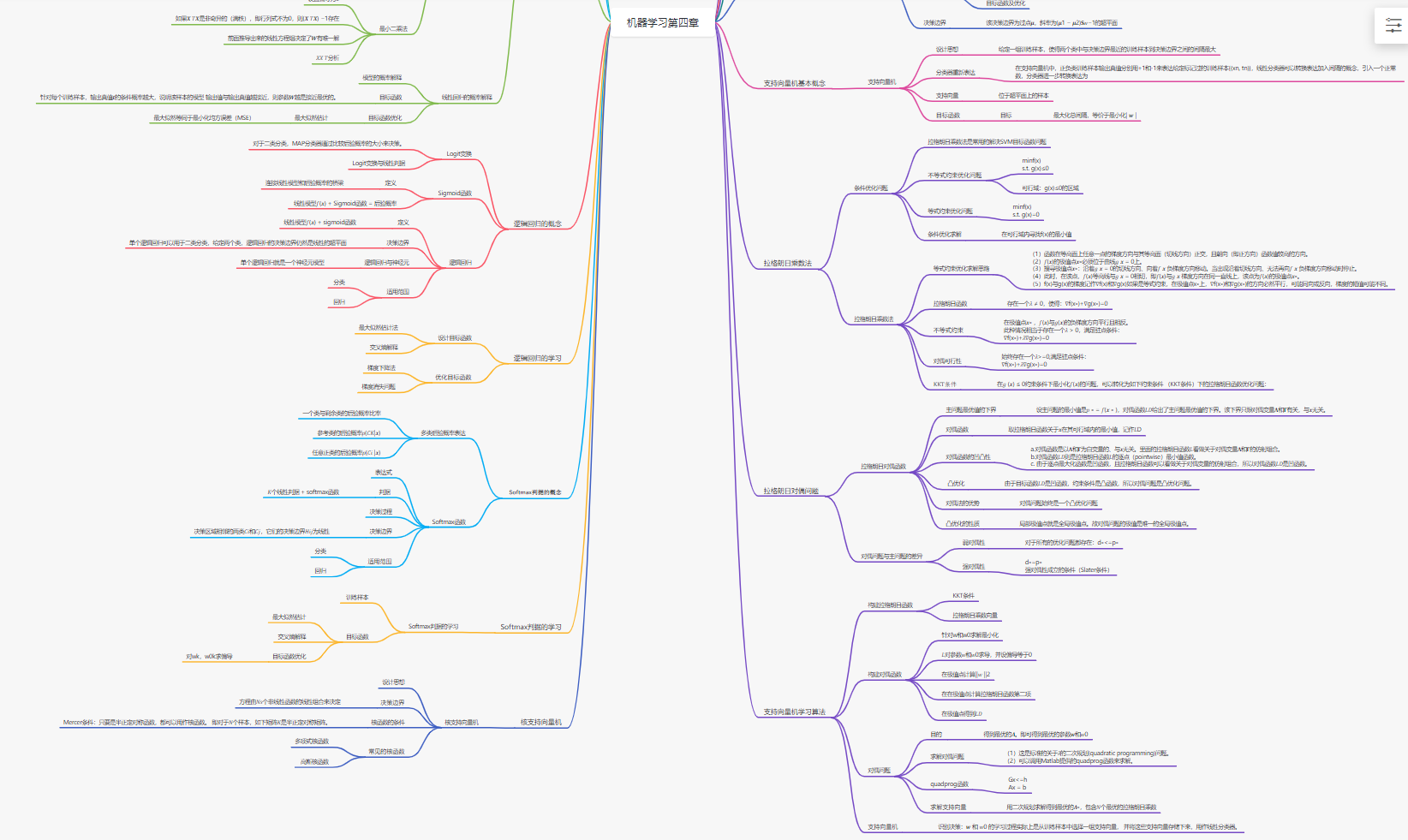
4.1、 线性判据基本概念
一.生成模型(Generative Model)
- 生成模型:给定训练样本 {𝒙𝑛},直接在输入空间内学习其概率密度函数𝑝(𝒙)。 2.优势与劣势
(1)优势:a.可以根据𝑝 𝒙 采样新的样本数据
b. 可以检测出较低概率的数据
(2)劣势:对于高维的x需要大量训练样本才能准确估计p(x),否侧容易出现维度灾难
二、判别模型
- 判别模型:给定训练样本 {𝒙𝑛},直接在输入空间内估计后验概率𝑝(𝐶𝑖|𝒙).
2.优势:快速直接、省去了耗时的高维观测似然概率估计。
三、线性判据
1.定义:如果判别模型𝑓(𝒙)是线性函数,则𝑓(𝒙)为线性判据;可以用于两类分类,决策边界是线性的;也可以用于多类分类,相邻两类之间的决策边界也是线性的。
2.优势:
(1)计算量少 (2)适用于训练样本较少的情况。
3.数学表达
(1)模型

(2)判别公式

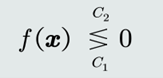
(3)决策边界方程

4.w的作用:决定了决策边界H的方向。
5.w0的作用:决定了决策边界的偏移量,使其能够满足两个类输出值分别为正负。 四、任意样本到决策边界的距离
四、任意样本到决策边界的距离
1.任意样本𝒙到决策边界的垂直距离(可以作为confidence score)为:
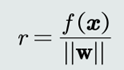
2.f(x) 是样本𝒙到决策面𝐻的代数距离度量。
4.2、线性判据学习概述
一、线性判据
1.学习和识别过程
(1)监督式学习过程:
基于训练样本{𝒙1, 𝒙2, … , 𝒙𝑁}及其标签{𝑡1,𝑡2, … ,𝑡𝑁} ,设计目标
函数,学习𝐰和𝑤0。
(2)识别过程:
将待识别样本x带入训练好的判据方程:
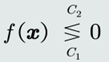
注:由于训练样本个数通常会远远大于参数个数(𝒘的维度+𝑤0的维度),所以线性判据满足条件的解不唯一。学习算法就是要找到一个最优解。
2.参数空间与解域
参数空间:由各个参数维度构成的空间。
参数的每个可能解相当于是参数空间的一个向量。
解域:在参数空间内,参数的所有可能解所处的范围。
二、目标函数
- 设计目标函数:目标函数反映了如何实现有效决策的核心思想。
常见的目标函数:误差(均方差)、交叉熵……
加入约束条件(例如,正则项):提高泛化能力。
2.目标函数的求解:最小化/最大化目标函数。
4.3 并行感知机算法
一、感知机算法:预处理
1.目的:根据标记过的训练样本 (𝒙𝑛,𝑡𝑛) ,学习模型参数:𝐰, 𝑤0
2.预处理步骤:

二、并行感知机
1.基本思想:被错误分类的样本最少。
2. 目标函数:针对所有被错误分类的训练样本(即输出值小 于0的训练样本),其输出值取反求和:

注:该目标函数是关于a的一次线性函数
3.参数更新

4.4 串行感知机算法
一、串行感知机
1.适用情况:训练样本是一个一个串行给出的。
2.目标函数
(1)思想:当前样本被错误分类的程度最小。
(2)目标函数:如果当前训练样本被错误分类,最小化其输出值取反:

(3)目标函数求解:
第一步,最小化目标函数:取关于参数向量𝒂的偏导。
第二步,偏导不含有𝒂,所以仍使用梯度下降法来求解𝒂。
3.收敛性:如果训练样本是线性可分的,感知机(并行和串行)算法理论上收敛于一个解。只保证了算法会停止。
4.步长决定收敛的速度、以及是否收敛到局部或者全局最优点。
5.加入Margin约束:
加入margin约束条件,将错误分类的标准改为:
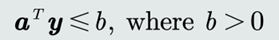
𝑏的作用:避免出现𝒂 = 𝟎的解,提高泛化能力。
4.5 Fisher线性判据
一、Fisher线性判据
1.基本原理:找到一个最合适的投影轴,使两类样本在该轴上投影的重叠部分最少,从而使分类效果达到最佳。最佳标准之一:投影后,使得不同类别样本分布的类间差异尽可能大,同时使得各自类内样本分布的离散程度尽可能小。
2.目标函数
(1)表征量的数学表达:
类间样本的差异程度:用两类样本分布的均值之差度量。
类内样本的离散程度:用每类样本分布的协方差矩阵表征。
(2)目标函数

(3)目标函数的优化

(4)最优参数解

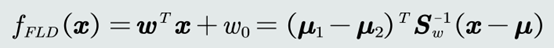
(5)决策边界:该决策边界为过点𝝁,斜率为(𝝁1 − 𝝁2)𝐒𝑤−1的超平面。
4.6、支持向量机基本概念
一.支持向量机
1.设计思想:给定一组训练样本,使得两个类中与决策边界最近的训练样本到决策边界之间的间隔最大。
2.支持向量概念:
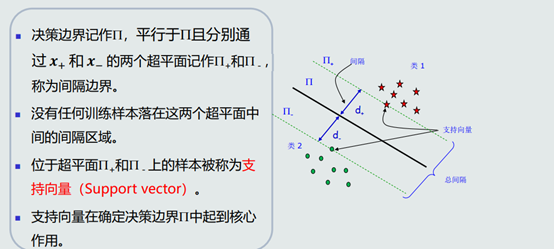
3.分类器重新表达
在支持向量机中,正负类训练样本输出真值分别用+1和-1来表达给定标记过的训练样本{(xn, tn)},线性分类器可以转换表达加入间隔的概念,引入一个正常数,分类器进一步转换表达为
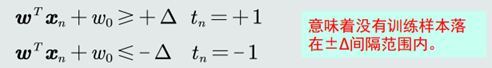
若设置正常数为1,则

4.支持向量
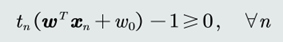
分类器新的表达中,当Xn是支持向量时,等式成立。
5.目标函数
(1)目标:最大化总间隔。
(2)最大化间隔,等价于最小化| 𝒘 |,所以目标函数设计为:
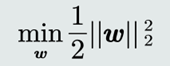
4.7、拉格朗日乘数法
一、条件优化问题
- 拉格朗日乘数法是常用的解决SVM目标函数问题
2.不等式约束优化问题
minf(x)
s.t. g(x)≤0
可行域:g(x)≤0的区域
3.等式约束优化问题
minf(x)
s.t. g(x)=0
4.条件优化求解
在可行域内寻找f(x)的最小值。
二、拉格朗日乘数法
- 等式约束优化求解思路
(1)函数在等高面上任意一点的梯度方向与其等高面(切线方向)正交,且朝向(即正方向)函数值较高的方向。
(2)𝑓(𝒙)的极值点𝒙∗必须位于曲线𝑔 𝒙 = 0上。
(3)搜寻极值点𝒙∗:沿着𝑔 𝒙 = 0的切线方向、向着𝑓 𝒙 负梯度方向移动。当出现沿着切线方向、无法再向𝑓(𝒙) 负梯度方向移动时停止。
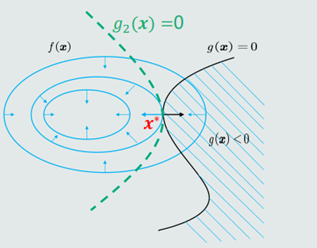
(4)此时,在该点,𝑓(𝒙)等高线与𝑔 𝒙 = 0相切,即𝑓(𝒙)与𝑔 𝒙 梯度方向在同一直线上,该点为𝑓(𝒙)的极值点𝒙∗。
(5)f(x)与g(x)的梯度记作∇f(x)和∇g(x)如果是等式约束,在极值点x∗上,∇f(x∗)和∇g(x∗)的方向必然平行,可能同向或反向,梯度的幅值可能不同。
2.拉格朗日函数
(1)因此,存在一个𝜆 ≠ 0,使得:
∇f(x∗)+∇g(x∗)=0
注:𝜆为拉格朗日乘子(可正可负),无符号限制。
(2)拉格朗日函数满足驻点条件和约束条件:
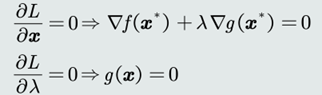
3.不等式约束
(1)情况1 :假设极值点𝒙∗落在了可行域内(不含边界),即极值点位于区域𝑔 𝒙 < 0范围内。此时在极值点x上:∇f(x∗)=0,g(x)<0
设置𝜆=0,此时:
L(x, 𝜆) = f(x)+ 𝜆g(x)
从而满足驻点条件且𝜆=0:
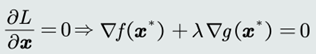
(2)情况2:假设极值点落在了可行域边界,即极值点位于区域𝑔 (𝒙) = 0区域。
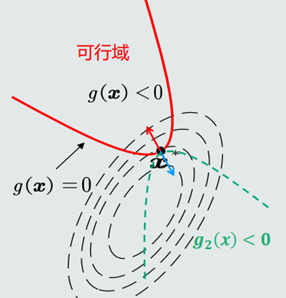
对于不等式约束,在极值点𝒙∗ ,𝑓(𝒙)与𝑔(𝒙)的负梯度方向平行且相反。
此种情况相当于存在一个𝜆 > 0,满足驻点条件:
∇f(x∗)+𝜆∇g(x∗)=0
4.对偶可行性
无论是𝑔 𝒙 < 0(𝜆 = 0)还是𝑔 𝒙 = 0(𝜆 > 0)的约束情况,始终存在一个𝜆 ≥ 0(对偶可
行性),满足:𝜆g(x) = 0,同时始终存在一个𝜆>=0,满足驻点条件:
∇f(x∗)+𝜆∇g(x∗)=0
5.KKT条件
在𝑔 (𝒙) ≤ 0约束条件下最小化𝑓(𝒙)的问题,可以转化为如下约束条件 (KKT条件)下的拉格朗日函数优化问题:
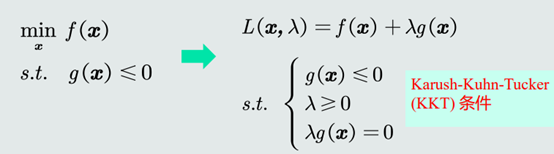
6.多个约束
可将多个约束下最小化f(x)的问题转为KKT条件下的拉格朗日函数优化问题
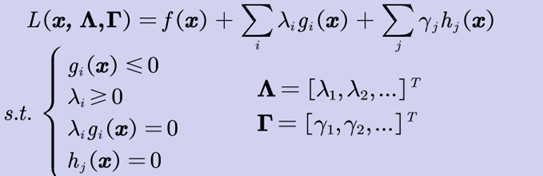
4.8、拉格朗日对偶问题
主问题:带约束的原问题等价于如下(关于𝒙的)无约束问题。
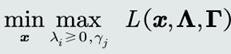
一、拉格朗日对偶函数
1.对偶函数

2.主问题最优值的下界
设主问题的最小值是𝑝 ∗ = 𝑓(𝒙 ∗ ),则得到
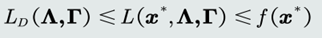
对偶函数𝐿𝐷给出了主问题最优值的下界。该下界只跟对偶变量𝚲和𝚪有关,与𝒙无关。
3.对偶函数的凹凸性
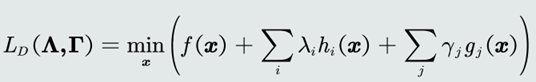
a.对偶函数是以𝚲和𝚪为自变量的、与𝒙无关。里面的拉格朗日函数𝐿看做关于对偶变量𝚲和𝚪的仿射组合。
b.对偶函数𝐿𝐷则是拉格朗日函数𝐿的逐点(pointwise)最小值函数。
c. 由于逐点最大化函数是凹函数,且拉格朗日函数可以看做关于对偶变量的仿射组合,所以对偶函数𝐿𝐷是凹函数。
4.凸优化:由于目标函数𝐿𝐷是凹函数,约束条件是凸函数,所以对偶问题是凸优化问题。
5.对偶法的优势:对偶问题始终是一个凸优化问题。
6.凸优化的性质:局部极值点就是全局极值点。故对偶问题的极值是唯一的全局极值点。
二、对偶问题与主问题的差异
1.弱对偶性
对于所有的优化问题都存在:d∗<=p∗
2.强对偶性:d∗=p∗
强对偶性成立的条件(Slater条件)

4.9支持向量机学习算法
一、构建拉格朗日函数
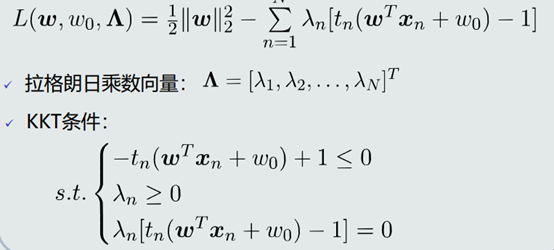
二、构建对偶函数
1.针对w和w0求解最小化
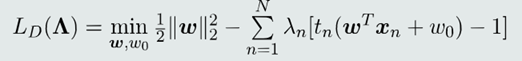
2.𝐿对参数𝑤和𝑤0求导,并设偏导等于0:

3.在极值点计算||𝑤 ||2

4.在在极值点计算拉格朗日函数第二项
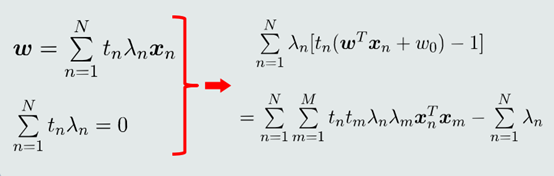
5. 在极值点得到𝐿𝐷

三、对偶问题
1.目的:得到最优的𝜦。即可得到最优的参数𝒘和𝑤0。
2.求解对偶问题:
(1)这是标准的关于𝜆的二次规划(quadratic programming)问题。
(2)可以调用Matlab提供的quadprog函数来求解。
3. quadprog函数
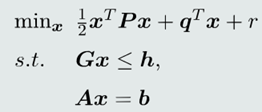
4.求解支持向量
(1)用二次规划求解得到最优的𝜦∗,包含𝑁个最优的拉格朗日乘数。
(2)根据KKT条件可知:

5.参数最优解
(1)根据找到的支持向量𝒙𝑛以及对应的拉格朗日乘子𝜆𝑛 ∗ 构建𝒘∗:
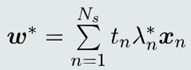
(2)根据支持向量机定义的约束条件,针对任意一个支持向量𝒙𝑠:
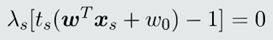
由此得到: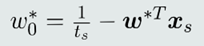
𝑤0通常由所有支持向量取均值得到: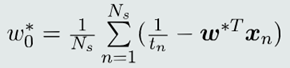
四、支持向量机
识别决策:𝒘 和 𝑤0 的学习过程实际上是从训练样本中选择一组支持向量, 并将这些支持向量存储下来,用作线性分类器。
4.10、软间隔支持向量机
一、设计思想
1.引入松弛变量𝜉𝑛,允许一些训练样本出现在间隔区域内,形成软间隔。
软间隔概念的引入,也使得线性SVM可以用于近似分类非线性数据。
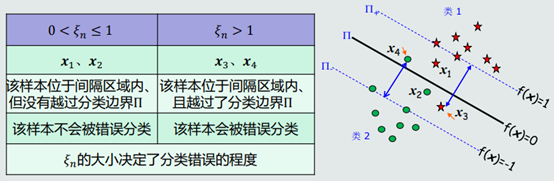
2. 给定标记过的训练样本 (𝒙𝑛,𝑡𝑛) ,引入 松弛变量𝜉𝑛后,分类器可以表达为如下 形式:
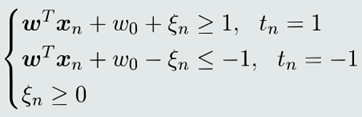
二、构建目标函数
1.目标函数
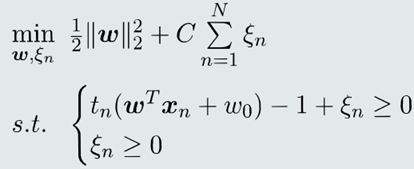
(1)目标函数变为2个自变量:𝒘和松弛变量𝜉𝑛。
(2)正则项的目的:意图使得错误分类最小。
(3)𝐶:正则项系数,表达对错误分类的处罚程度。 𝐶越大,说明惩罚 程度大,训练精度高,但可能过拟合程度也高。
三、构建拉格朗日函数
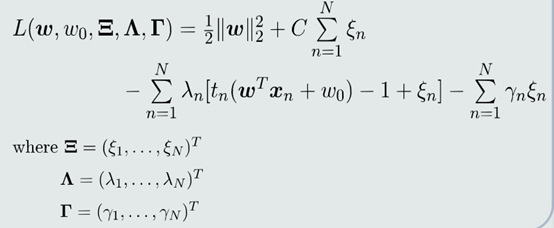
2.KKT条件
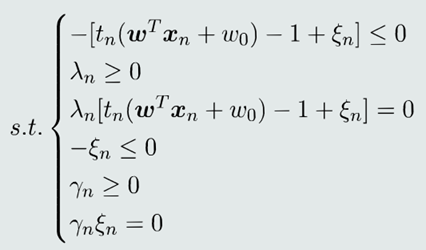
四、构建对偶函数
1.对偶函数
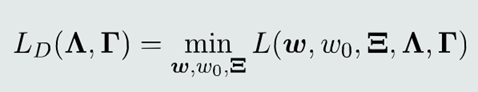
2. 针对𝑤、𝑤0求解最小化
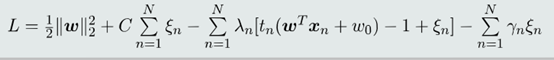
(1)求拉格朗日函数𝐿关于𝒘,𝑤0和𝜉𝑛的偏导,并设偏导为0:
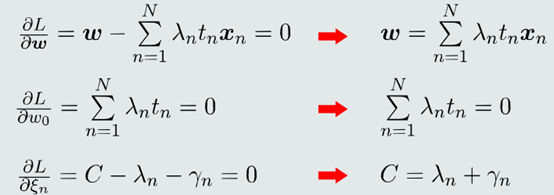
(2)在极值点消去𝑤、𝑤0
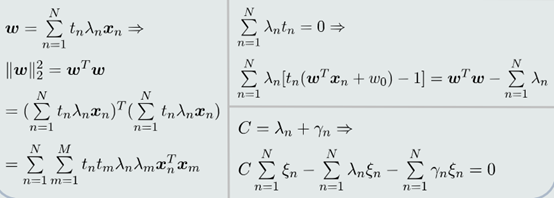
(3)在极值点得到对偶函数 𝐿D

3.对偶问题
(1)最大化该对偶函数得到最优的𝜦。

(2)得到最优的𝜦。即可得到最优的参数𝒘和𝑤0。
4.支持向量
(1)求解支持向量
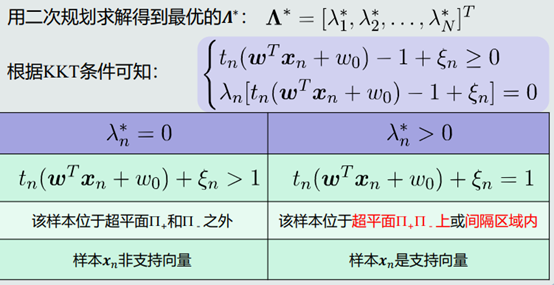
(2)支持向量分析

5.参数最优解

6.决策过程
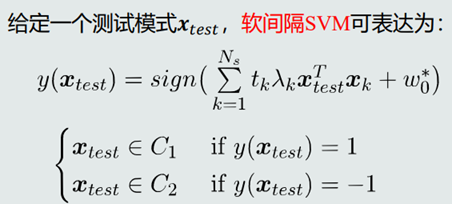
4.11、线性判据多类分类
一、One-to-all策略
1.基本思想
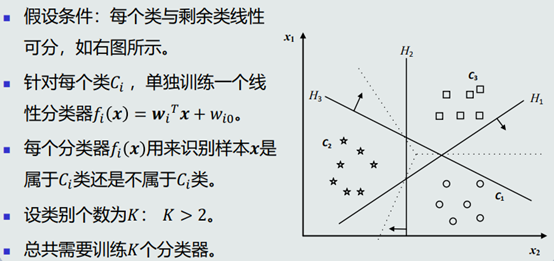
- 判别公式、决策边界
(1)判别公式

(2)决策边界

(3)训练样本选择
对于每个分类器𝑓𝑖(𝒙) ,属于𝐶𝑖类的训练样本作为正样本, 其余类别的训练样本作为负样本。可是会导致每个分类器正负类样本个数不均衡。
二、线性机
1.基本思想
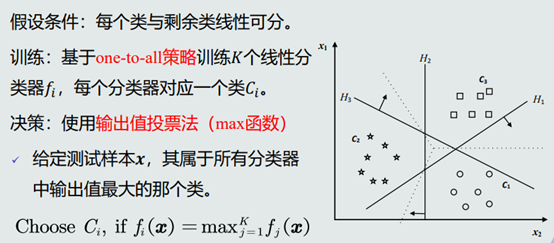
2.决策过程数学表达
(1)线性机的决策过程相当于:将输入特征𝒙直接映射到类别标签𝑙。
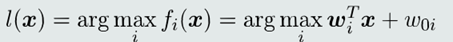
线性机 = 𝐾个线性模型 + 一个max函数。
(2)综合𝐾个线性模型, 𝐾个权重向量𝒘𝑖写成矩阵𝑾,决策过程可以表达为:
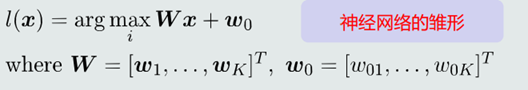
3.决策边界
(1)通过max函数的引入,线性机将特征空间最终分为𝐾个决策区域。
(2)决策区域相邻的两类𝐶𝑖和𝐶𝑗,它们的决策边界𝐻𝑖𝑗为(下图虚线所示):
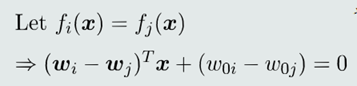
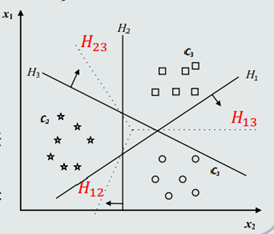
(3)决策边界𝐻𝑖𝑗垂直于超平面(𝒘𝑖 − 𝒘𝑗)
三、One-to-one策略
1.基本思想
(1)针对每两个类𝐶𝑖 和𝐶𝑗 ,训练一个线 性分类器: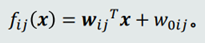
𝐶𝑖类真值为正;𝐶𝑗类真值为负。
(2)总共需要训练𝐾 𝐾 − 1 /2个分类器。
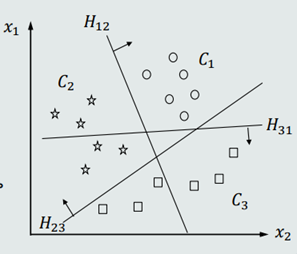
2.训练样本选择
对于每个分类器𝑓𝑖𝑗 (𝒙) ,属于𝐶𝑖类的训练样本作为正样本,属于𝐶𝑗类的训练样本作为负样本。避免了one-to-all策略正负类样本个数不均衡的问题。
3. 判别公式&决策边界
(1)给定测试样本𝒙,如果所有𝐶𝑖 相关的分类器输出都为正,则𝒙属于𝐶𝑖 :
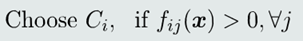
(2)决策边界
𝐶𝑖类与剩余类的决策边界:所有𝐻𝑖𝑗正半边的交集。
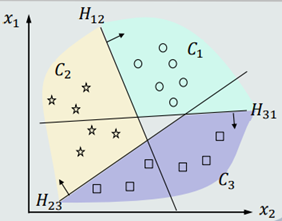
4.优势:
适用于一些线性不可分的情况, 从而实现非线性分类。
与one-to-all策略相比,不再有重叠区域。
四、总结
- 使用线性判据进行多类分类,本质上是利用多个线性 模型组合而成一个非线性分类器。
- 因此,决策边界不再是由单个超平面决定,而是由多 个超平面组合共同切割特征空间。
4.12、线性回归
一、输入数据
- 输入样本:个数与特征维度的关系
(1)每个输入样本特征为𝑃维。样本个数为𝑁。
(2)Tall数据:𝑁 ≫ 𝑃,所有训练样本的输入和真值输出 构成一个超定方程组。可以使用线性回归来学习。
(3)Wide数据:𝑁 ≪ 𝑃,所有训练样本的输入和真值输 出构成一个欠定方程组。
二、线性回归模型表达
- 输出单维度

- 分列方程:

- 扩展:输出多维度

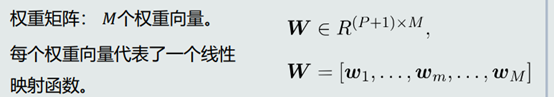
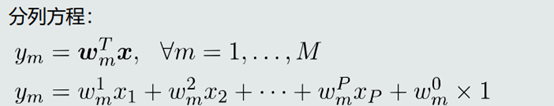
4.模型对比
(1)线性回归
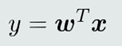
线性回归关注输出值的具体数值 (连续值)。
所以,将输入空间+输出空间放 在一起研究其线性映射方程。
(2)线性判据
线性判据关注输出值的正负符号 (离散二值)。
所以,在输入空间研究其决策边 界方程(它是线性的):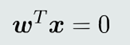
三、线性回归模型学习
1.训练样本
(1)给定𝑁个训练样本
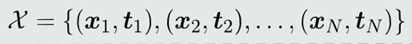

(2)𝑁个样本的输入表达:
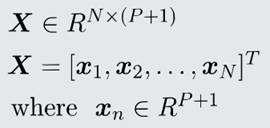
(3)𝑁个样本的输出真值表达:
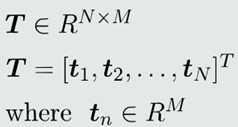
2.目标函数
(1)最小化均方误差
如果参数𝑾是最优的,意味着对每个样本(𝒙𝑛, 𝒕𝑛)而言,模型的输出 值𝒚𝑛与标定的输出真值𝒕𝑛之间的差值最小。
因此,目标函数可以使用均方误差(sum-of-squares error) ,即最小 化均方误差(minimize square error, MSE):
3.对比
(1)线性判据:主要判断预测的输出值与真值在符号上的差异。
感知机:被错误分类的样本的输出值之和。虽然输出值代表错误的程度,但是不考虑正确分类的正确程度。
(2)线性回归:比较预测的输出值和真值在数值上的差异。
4.目标优化
(1)展开目标函数
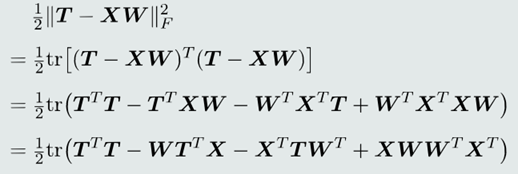
(2)对参数𝑾求偏导
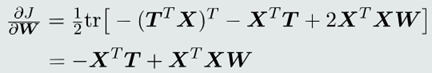
5. 梯度下降法
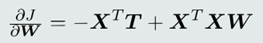
采用梯度下降法更新𝒘和𝑤0:
(1)设当前时刻为𝑘,下一个时刻为𝑘 + 1
(2)𝜂为更新步长
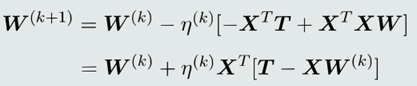
6. 最小二乘法
(1)设置偏导为0:
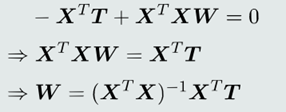
(2)如果𝑿 𝑇𝑿是非奇异的(满秩),即行列式不为0,则(𝑿 𝑇𝑿) −1存在。
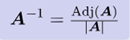
(3)前面推导出来的线性方程组决定了𝑾有唯一解:
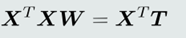
(4)𝑋𝑋 𝑇分析
如果𝑁 ≫ 𝑃 + 1,即Tall数据,则rank(𝑿 𝑇𝑿) ≤ 𝑃 + 1(可能满秩), 因此,𝑿 𝑇𝑿是非奇异阵的可能性较高。
如果𝑃 + 1 ≫ 𝑁,即Wide数据,则rank(𝑿 𝑇𝑿) ≤ 𝑁(不满秩),可得 𝑿 𝑇𝑿肯定是奇异矩阵。
四、线性回归的概率解释
-
模型的概率解释

2.目标函数
针对每个训练样本,输出真值𝒕的条件概率越大,说明该样本的模型 输出值与输出真值越接近,则参数𝑾越是接近最优的。
因此,给定𝑁个训练样本,似然函数为输出真值𝒕的条件概率乘积。该 似然函数即为目标函数。最大化该目标函数。 -
目标函数优化
(1)最大似然估计
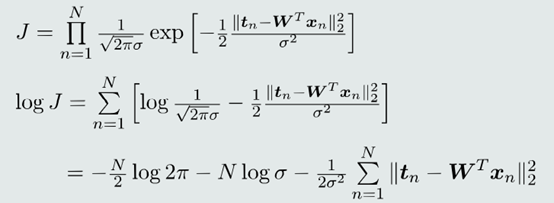
(2)最大似然VS MSE

结论:最大似然等同于最小化均方误差(MSE)。
4.13、逻辑回归的概念
一、典型模型的属性
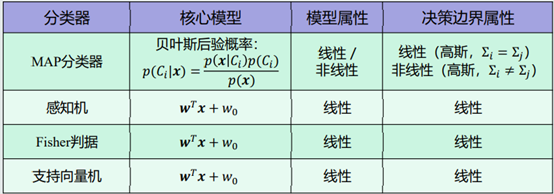
二、Logit变换
1.对于二类分类,MAP分类器通过比较后验概率的大小来决策。
在每类数据是高斯分布且协方差矩阵相同的情况下, 𝒙属于𝐶1类的后验概 率与属于𝐶2类的后验概率之间的对数比率就是线性模型𝑓(𝒙)的输出。
2. Logit变换与线性判据
设𝐶1代表正类(即线性判据输出大于0的类),𝐶2代表负类。
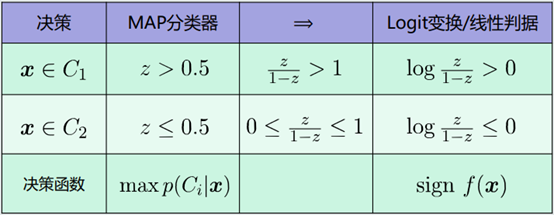
三、Sigmoid函数
1.定义:连接线性模型和后验概率的桥梁
2.线性模型𝑓(𝒙) + Sigmoid函数 = 后验概率
四、逻辑回归
1.定义:线性模型𝑓(𝒙) + sigmoid函数。
2.决策边界:单个逻辑回归可以用于二类分类,给定两个类,逻辑回归的决策边界仍然是线性的超平面。
3.逻辑回归与神经元:单个逻辑回归就是一个神经元模型
多个逻辑回归(即多个同层神经元)可应用于多类分类,使用 max函数做决策(即基于one-to-all的线性机):
4.适用范围
(1)分类:
狭义上看,每个类的数据都是高斯分布且分布的协方差矩阵相同。
广义上看,每个类的数据分布可以是非高斯,甚至是多模态分布。
(2)回归:可以拟合sigmoid形式的非线性曲线
5.总结:
(1)逻辑回归本身是一个非线性模型。
(2)逻辑回归用于分类:仍然只能处理两个类别线性可分的情况。逻辑回归比线性模型向前迈进了一步。
(3)逻辑回归可以拟合有限的非线性曲线。
4.14、逻辑回归的学习
一、设计目标函数
1.最大似然估计法
(1)给定单个输入样本𝒙,模型输出的类别标签𝑙可以看做一个随机变量。
(2)基于最大似然估计策略,经过一系列的推导,最终得到的目标函数为:
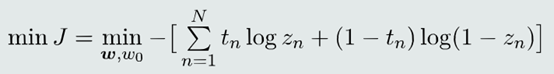
3.交叉熵解释
(1)训练目标:给定单个样本𝒙𝑛,希望模型预测输出的概率分布𝑝 (𝑙𝑛|𝒙𝑛)符合输出真 值的概率分布𝑞(𝑙𝑛|𝒙𝑛),即两种分布的差异程度最小。
(2)交叉熵可以用来度量两种分布的差异程度。
(3)目标函数:
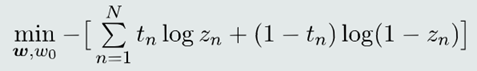
二、优化目标函数
- 梯度下降法:分别对参数w和w0求导,然后更新参数
- 梯度消失问题
当𝑦 = 𝒘𝑇𝒙 + 𝑤0较大时,sigmoid函数输出𝑧会出现饱和:输入变化量∆𝑦很大时, 输出变化量∆z很小。
在饱和区,输出量𝑧接近于1,导致 sigmoid函数梯度值接近于0,出现梯度 消失问题。
3.参数初始化:参数𝒘尽量选择较小的初始值,避免出现梯度消失问题。
4.迭代停止:在达到一定训练精度后,提前停止迭代,可以避免过拟合。
4.15 Softmax判据的概念
一、多类后验概率表达
- 一个类与剩余类的后验概率比率
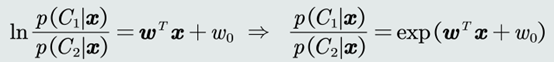
- 参考类的后验概率𝑝(𝐶𝐾|𝒙)
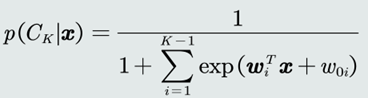
3.任意正类的后验概率𝑝(𝐶𝑖 |𝒙)
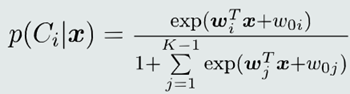
对于多类分类(𝐾 > 2), 𝐾个线性模型也跟每个类对应 的后验概率建立起了联系。
二、Softmax函数
1.表达式:
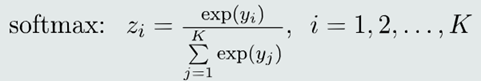
2. 该后验概率计算方法被称作softmax函数:
如果一个类𝐶𝑖对应的𝑦𝑖(即线性模型的输出)远远大于其他类的, 经过exp函数和归一化操作,该类的后验概率𝑝(𝐶𝑖 |𝒙)接近于1,其 他类的后验概率接近于0,则softmax决策就像是一个max函数。该函数又是可微分的,所以称作“软最大值函数” 。
3.判据:𝐾个线性判据 + softmax函数。
4.决策过程:给定测试样本𝒙,经由线性模型和softmax函数计算𝐾个类对应的 后验概率, 𝒙属于最大后验概率对应的类别。
5.决策边界:决策区域相邻的两类𝐶𝑖和𝐶𝑗,它们的决策边界𝐻𝑖𝑗为线性。
6. Softmax判据与神经网络
相当于由𝐾个神经元组成的神经网络输 出层,每个神经元输出值代表属于该类的后验概率𝑝(𝐶𝑖|𝒙) ∈ [0,1]。
7.适用范围
(1)分类:前提是每个类和剩余类之间是线性可分的。
(2)回归:范围是可以拟合指数函数(exp)形式的非线性曲线。
三、总结
- Softmax判据本身是一个非线性模型。
- Softmax判据用于分类:只能处理多个类别、每个类别与剩余类线 性可分的情况。但是, Softmax判据可以输出后验概率。
- Softmax判据可以输出有限的非线性曲线。
4.16 Softmax判据的学习
一、Softmax判据的学习
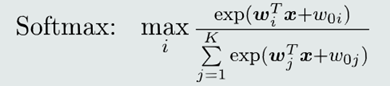
1.训练样本:给定𝐾个类别,共𝑁个标定过的训练样本。
2.目标函数:
(1)最大似然估计

(2)交叉熵解释

(3)目标函数优化:对wk,w0k求偏导
4.17、 核支持向量机(Kernel SVM)
一、核支持向量机
1.设计思想
(1)如果样本在原始特征空间(𝑋空间)线性不可分,可以将这些样本 通过一个函数𝜑映射到一个高维的特征空间(Φ空间),使得在这 个高维空间,这些样本拥有一个线性分类边界。
(2)如果在高维空间Φ两个类是线性可分的,则可以应用线性SVM来实现 𝑋空间的非线性分类
2. 决策边界:方程由𝑁𝑠个非线性函数的线性组合来决定。因此,在𝑋空间是一条非线性边界。
3. 核函数的条件
Mercer条件:只要是半正定对称函数,都可以用作核函数。 即对于𝑁个样本,如下矩阵𝐾是半正定对称矩阵。
4.常见的核函数
(1)多项式核函数
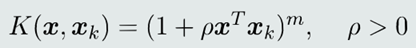
(2)高斯核函数
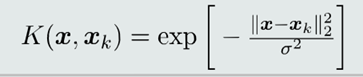
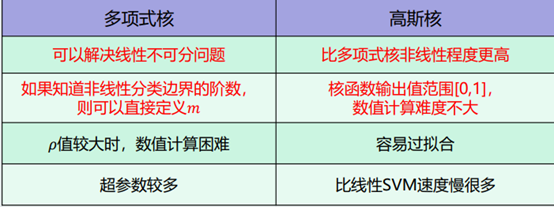
5.核函数优缺点
二、总结
1.构建非线性
(1)需要有非线性的基函数,例如,核函数。
(2)需要多个这样的基函数进行组合(可以是线性组合)。
2.组合方式
(1)并行组合:Kernel SVM
(2)串行组合



