CS:APP Chapter 6 存储器层次系统-读书笔记
存储器层次系统
笔记,应该不是一个大而全的文件,笔记应该是提纲挈领,是对思想的汇总浓缩,如果追求详实的内容反而是丢了初心。
计算机是抽象的,它的设计者努力让计算机变得简单,在设计上高度抽象,而计算机的存储系统就是这样一个对用户透明的部分,程序员布恩那个直接操作内存的控制,但是可以通过理解内存的组织结构,运行特点编写对内存友好的程序,编写具有较好时间局部性,空间局部性的程序。
存储器是多样的,从高速缓存 Cache 到主存,再到磁盘,机械硬盘,固态硬盘,他们是各有特色,一般来说,越接近 CPU 的存储设备,价格约昂贵,成本越高,其容量也越小,而越靠近磁盘的存储设备,价格越低,容量越大,一般而言,我们可以把k层的设备看作是k+1层设备的缓存,例如 Cache 是主存到 CPU 之间的缓存,而主存是磁盘的缓存。
形成这种存储结构的原因是计算机软件程序具有局部性,它往往会在短时间之内访问同一块区域的数据,也就是说相对而言较少跳跃着使用数据,因此,使用一个较小容量的缓存就能覆盖一大片可能出现下一时刻要用的数据,进一步提高处理器获取需要数据的效率。
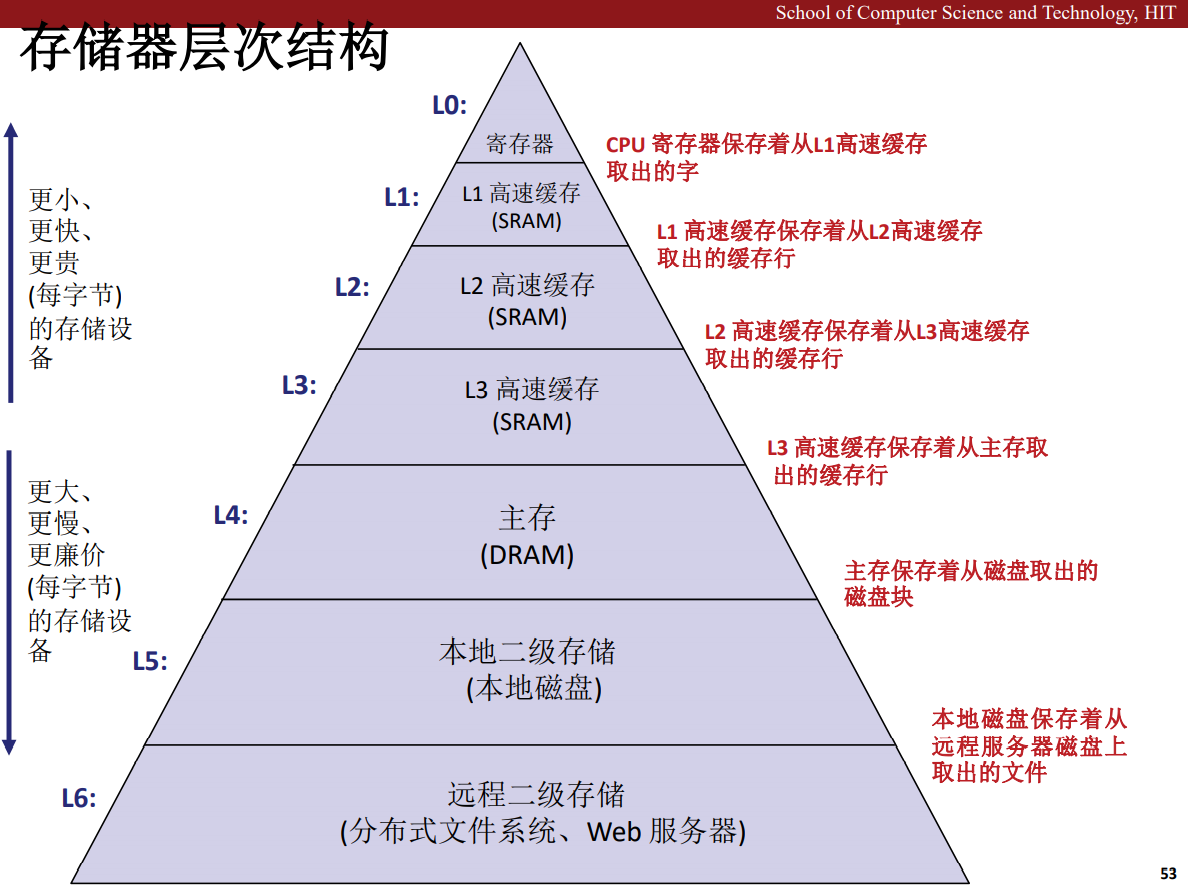
一般而言,所有的存储设备的单位都是字节,也就是 Byte 缩写成 B,大写。
机械硬盘
计算磁盘容量
容量 = (字节数 / 扇区) * (平均扇区数 / 磁道) * (磁道数 / 面) * (面数 / 盘片) * (盘片数 / 磁盘)

这个计算比较简单,只要把单位一个个约掉就行了。
从小到大分别是:字节,扇区,磁道,面,盘片,磁盘。
磁盘读取

平均时间
$ 访问时间 = 寻道时间 + 平均旋转延迟(旋转时间)+ 数据传输时间 $
寻道时间 (Seek time)
-
读 / 写头移动到目标柱面所用时间,这个时间有可能是题目中直接给出的,我们无法计算寻道时间。
-
通常寻道时间为:3—9 ms
旋转延迟 (Rotational latency)
-
旋转盘面使读 / 写头到达目标扇区上方所用时间
-
平均旋转延迟 = 1/2 x 1/RPMs x 60 sec/1 min (RPM:转 / 分钟)
-
通常 平均旋转延迟 = 7,200 RPMs
数据传输时间 (Transfer time)
-
读目标扇区所用时间
-
数据传输时间 = 1/RPM x 1/(平均扇区数 / 磁道) x 60 secs/1 min

每次读取的是一个扇区,所以只需要计算读取每个扇区的平均时间就行了,读取的时间是远远小于磁头的旋转时间的。而且其中 \(\frac {60}{7200}(秒 / 磁道) \),注意这里的单位,一个磁道就是一个面的一整圈
设计使用高速缓存
那么,我们应该如何来设计一个高速缓存系统呢?
-
了解计算机程序可利用的存储特性:局部性。
-
使用不同的高速缓存 - 主存映射方式来组织数据。
-
如何利用存储器系统为我们准备好的局部性优化特点编写缓存友好的代码。
局部性
-
时间局部性(Temporal ):最近被访问过的(指令或数据)可能会再次被访问(比如循环,局部变量)
-
空间局部性(Spatial ):被访问的存储单元附近的内容可能很快也会被访问(比如数组,顺序访问内存,顺序读取指令等)
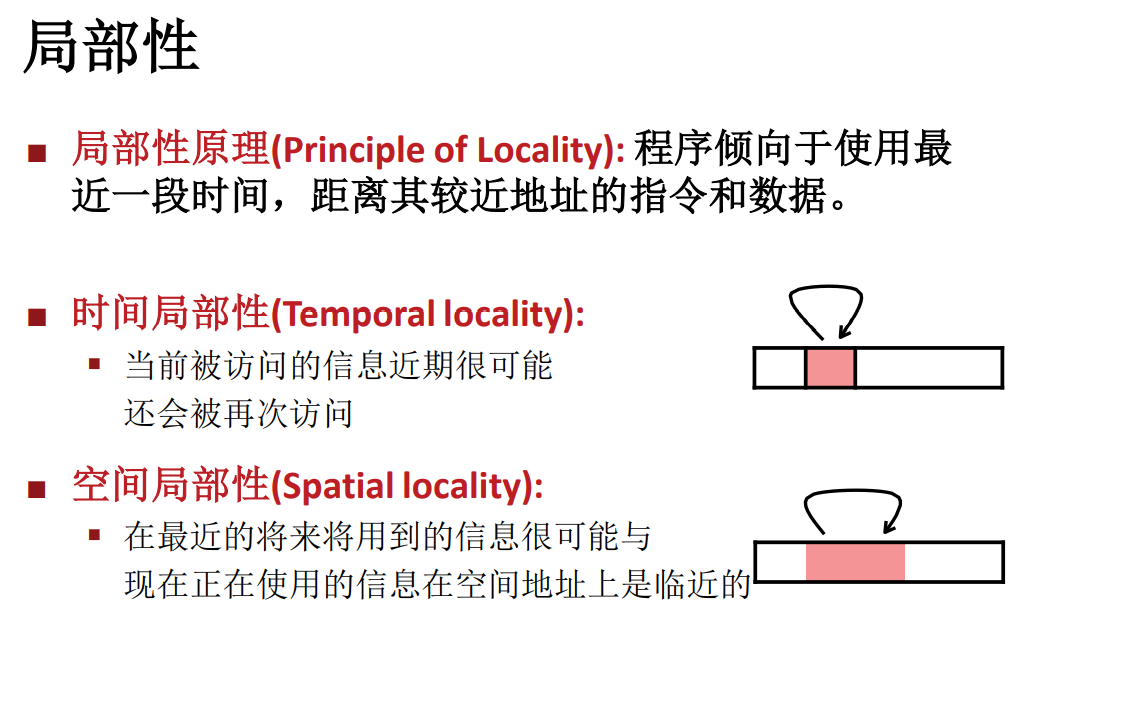
局部性说明,一段时间内,计算机往往倾向于访问使用读写某一小块的内存 / 数据,这块数据以及这块数据附近的数据都有比其他区域更高的使用概率,因此当我们缓存这部分的时候就能让效率得到更显著的提升。
int sum_array_rows(int a[M][N])
{
int i, j, sum = 0;
for (i = 0; i < M; i++)
for (j = 0; j < N; j++)
sum += a[i][j];
return sum;
}
这段代码具有较好的空间局部性与时间局部性,因为这里使用了一个局部变量来暂存加法的结果,并且其访问数组的方式也是遵循数组在内存中存储的特点,这让缓存能够更加高效的命中。
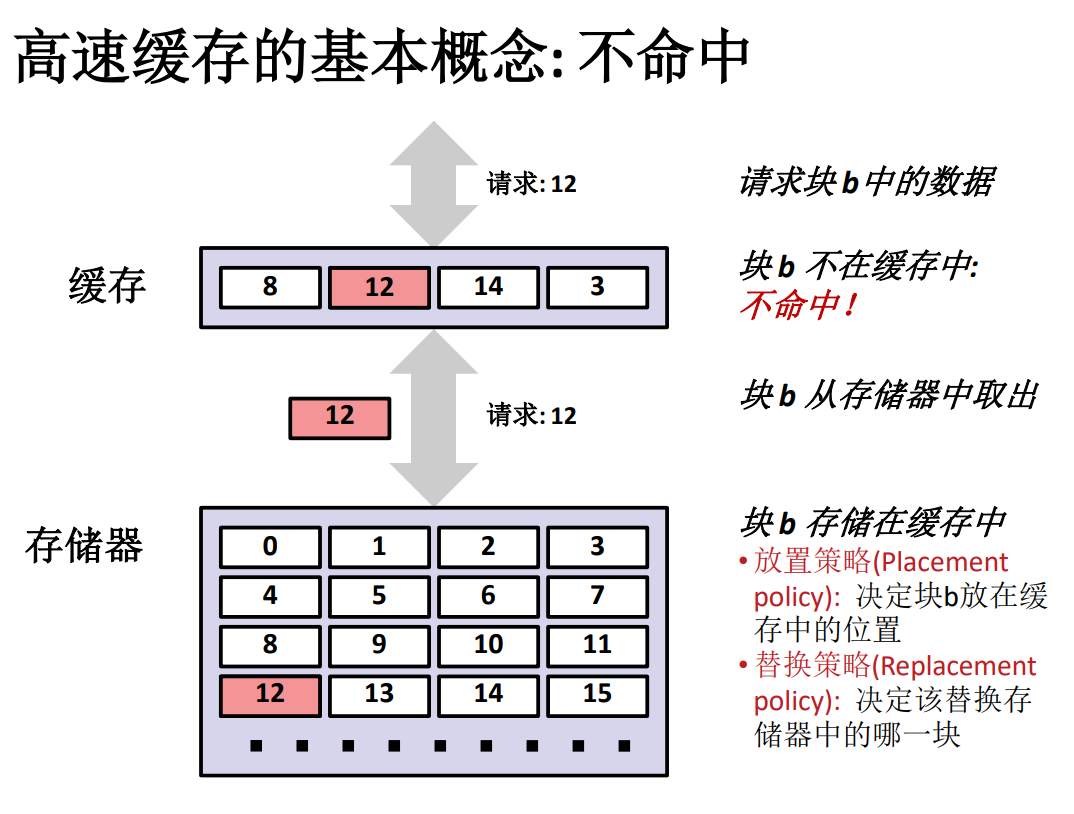
而事实上,总会出现缓存不命中的情况,并且导致缓存不命中的原因也有很多种。
缓存不命中
-
冷不命中。当缓存为空的时候,所有数据请求都不能在缓存中找到对应的缓存好的数据,一般来说这是在计算机刚刚启动的时候才会发生这样的情形。这种类型被称为冷不命中。
-
冲突不命中。因为缓存大小有限,而主存要比缓存要大得多得多,因此不可能实现缓存不重复地映射到所有主存单元,因此就会出现不同的主存单元映射到相同的缓存块中。例如某种缓存映射策略为:第 k+1 层的块 i 必须放置在第 k 层的块 (i mod 4) 中,当缓存足够大,但是被引用的对象都映射到同一个缓存块中时候就是冲突不命中。冲突的例子:程序请求块 0, 8, 0, 8, 0, 8, .... 这时每次请求都不命中。
-
容量不命中。处理器要处理的工作集的大小远远大于缓存的大小时,计算把全部的工作集内容读取到缓存中来,也有可能发生不命中,此时被称为容量不命中。
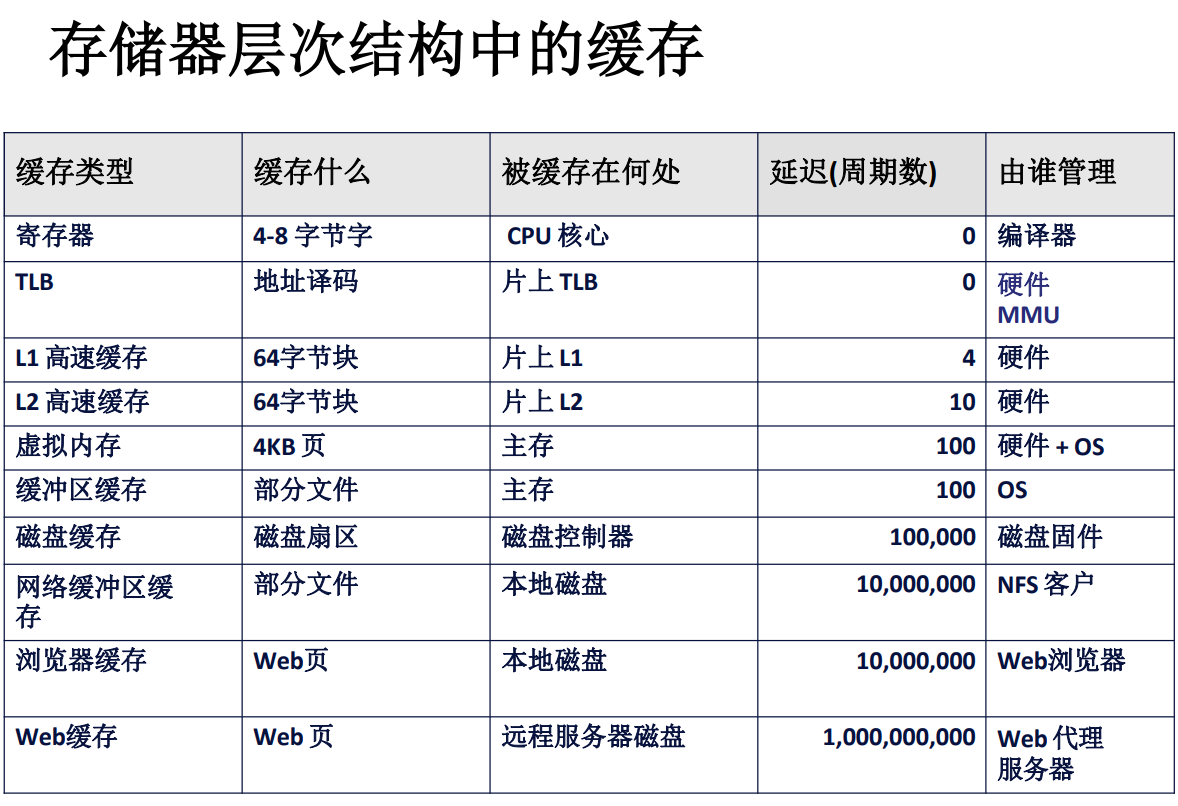
如果说第一部分的主要内容是磁盘,高速缓存的概念的话,那第二部分就主要是高速缓存的组织结构,以及如何利用高速缓存针对性地编写代码。

寄存器是最靠近计算单元的存储设备,因此,它的读取写入速度也是所有设备中最快的,高速缓存的速度稍慢,介于寄存器与内存之间,高速缓存通过总线接口与外部的存储设备沟通,经由系统总线、I/O桥、内存总线与主存相连接。
CPU 其实也并不需要了解缓存到底是怎样运作的,它只管给出自己当前需要的数据的主存地址,也就是说 CPU 只知道数据应该在内存里,而这个主存地址在传输过程中会经过高速缓存,高速缓存会自动判断这个地址所代表的数据是否在缓存中,一般来说是通过计算主存地址中的信息,利用高速缓存的映射策略来得到该地址在缓存中对应的位置,并将主存地址中的 tag 与缓存中那个位置的 tag 进行比较,如果一致就说明是对的。
但是并不是所有的主存内容都恰好在缓存中,只有极少数的一部分(缓存比主存要小的多的多)会存放在主存中。因此总会有没命中的情况,在这种情况下就需要从主存中读取需要的数据。
读取完成之后有两步并行操作,1️⃣ 是把 CPU 需要的数据赶紧送到 CPU 那里去,2️⃣ 是把刚送过来的数据存放在缓存中,因为计算机程序具有时间局部性,在不远的未来有比较大的可能接着访问这个内存单元,因此缓存起来可以应对未来的读取需求。

上面是高速缓存系统的一个理想流程图,要实现整个过程需要很多的细节方面的考量。
-
主存如何分块,Cache 如何分块或分区分行
-
主存块与缓存之间如何映射
-
如果缓存放满了的话如何淘汰缓存中的块
-
写入主存的请求如何正确处理以保证缓存与主存之间的一致性
-
如何根据主存地址计算缓存中的数据位置并比对
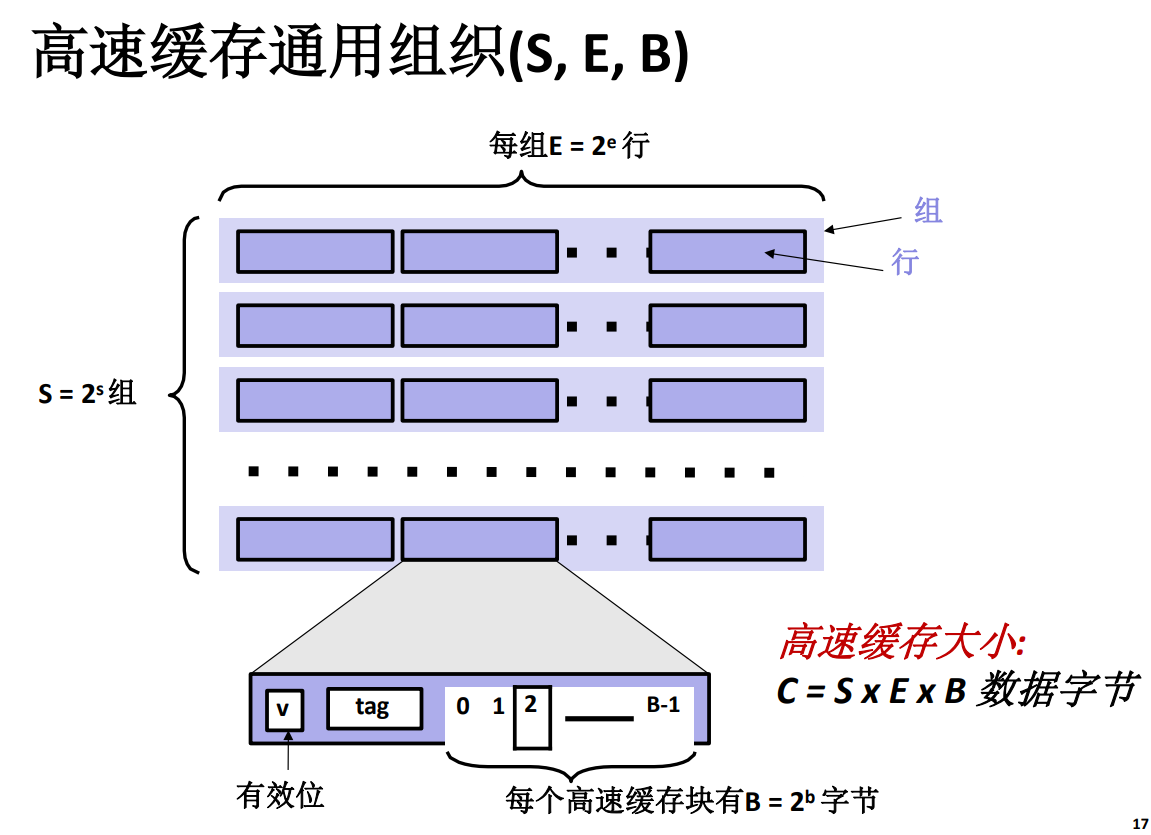
高速缓存通用组织
-
S 代表 Cache Set,也就是缓存组
-
E 代表 Cache Line,也就是缓存行
-
B 代表组成每一行的数据块的字节数目 \(B=2^b\)。
要注意,高速缓存中最大的分组就是 Cache Set,而主存地址中的 s 也就是组索引,而最小的数据包裹单位是数据行,包含真正数据的是数据块,数据块中没有有效位,标记位之类的信息,里面只有数据!
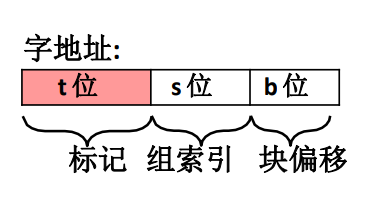
不管缓存的映射策略是什么样的,CPU 发出的主存地址格式一定是一致的不会因为缓存的映射策略而出现不同格式的主存地址,一般来说主存地址是由 3 部分组成。
-
\(t\) 代表标记
-
\(s\) 代表组索引
-
\(b\) 代表块偏移量
当然这些不同部分在不同策略中的含义也是不一样的。不过大体上都是这几块。
直接映射高速缓存
这种映射策略的最主要特点是它每一个缓存组中只有一个高速缓存行,也就是 \(E=1\),代表每一个主存块仅仅会映射到其中一个 Cache 的固定一行。
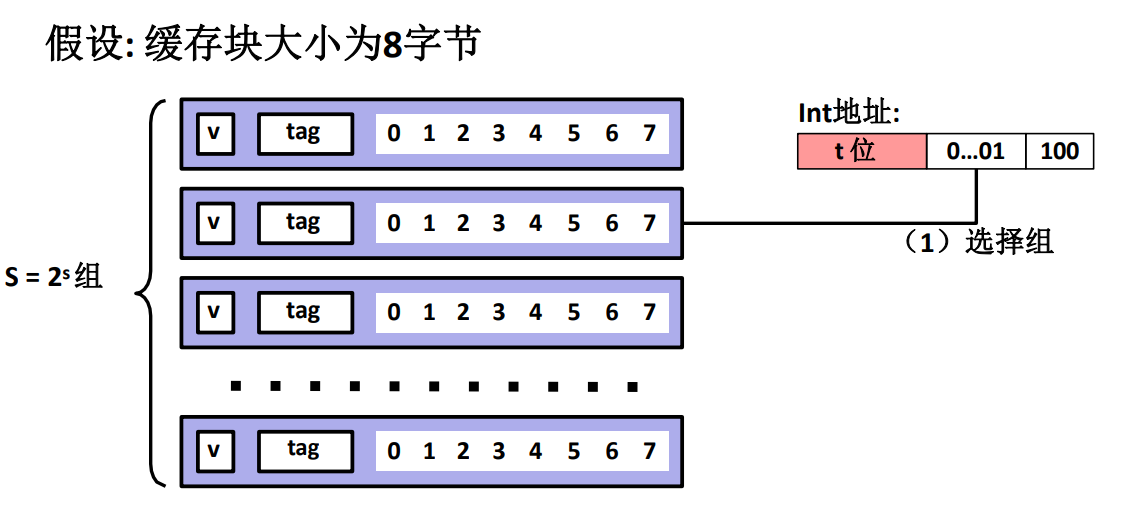
而每一行并不是每个位都是数据,而是也分成了很多部分。
-
\(v\) 代表有效位 \(valid\)。
-
\(tag\) 代表标记
-
之后的数字代表剩下的数据,所有数据代表了一个缓存块,它有 \(B\) 个字节,而 CPU 需要的数据在哪个字节由主存地址中的数据偏移量指出!
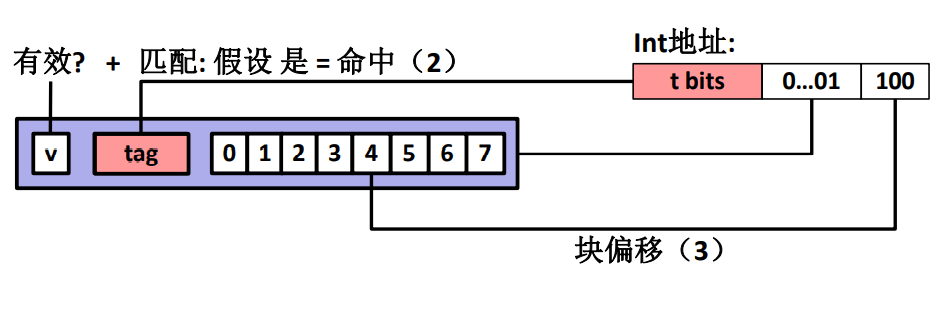
同时要注意,并不是只取出其中那一个字节,100 代表的是 4,这个数字是要取出的数据的起始位置,然后根据数据类型计算剩下的数据长度,然后再把全部数据完整的拿出来。

-
有效的标记位
-
正确匹配的 tag
-
根据偏移量与数据类型长度取出数据
这样三部分走完才算是完成了直接映射缓存器的读取过程。
如果没有找到匹配的行,就从主存中读取然后直接驱逐替换,不用考虑是否什么优先级的关系,反正只有一行。
E - 路组相联高速缓存
此处简单取 \(E=2\) ,也就是每组有两个数据行。
当使用 E - 路组相联高速缓存时,每个主存块都映射到 Cache固定组的任意一行,有点像直接映射缓存的链表,也就是每一个组里面是一个链表!然后数据写入的时候是先到先写入,因此位置是不固定的。
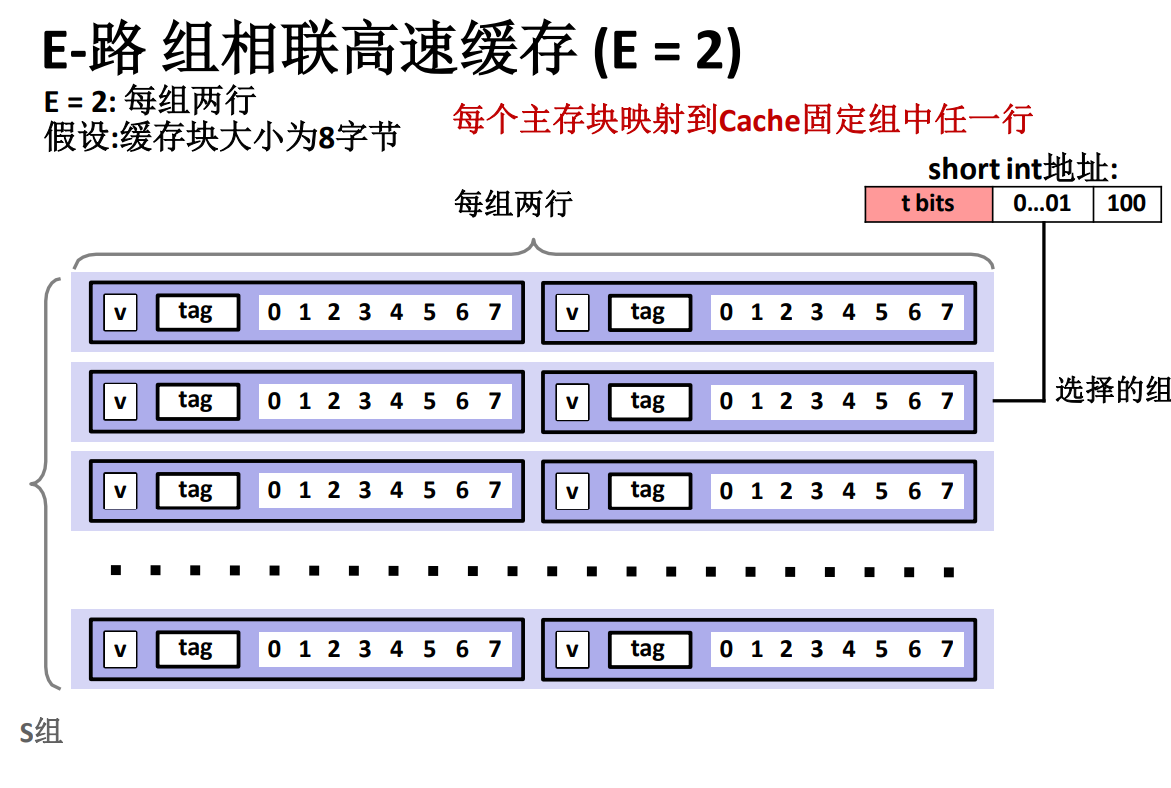
而 E - 路组相联高速缓存的查找过程跟直接组相联也比较类似,不过它并不能保证 \(O (1)\) 的时间复杂度,因为对应的数据块的位置并不是固定的,所以不会一下子直接找到,通过主存地址中的组索引 \(s\) 部分可以定位到这个主存块对应的组,然后对这个组中所有的行进行遍历,找到 tag 和主存地址中的 tag 一致的行,然后使用同样的办法读取需要的数据。


当不匹配的时候,需要在主存地址给出的组中找到一行用来存放主存地址对应的那段数据,由于一个组中有多个行,所以要考虑驱逐替换哪一行!
替换策略:
-
随即替换
-
替换最近最少使用的那行
高速缓存的写入问题
-
存在多个数据副本:
- L1, L2, L3, 主存,磁盘
-
在写命中时要做什么?
-
直写 (立即写入存储器)
-
写回 (推迟写入内存直到行要替换)
- 需要一个修改位 (和内存相同或不同的行)
-
-
写不命中时要做什么?
-
写分配 (加载到缓存,更新这个缓存行)
- 好处是更多的写遵循局部性
-
非写分配 (直接写到主存中,不加载到缓存中)
-
-
典型的
-
直写 + 非写分配
-
写回 + 写分配
-
高速缓存实例
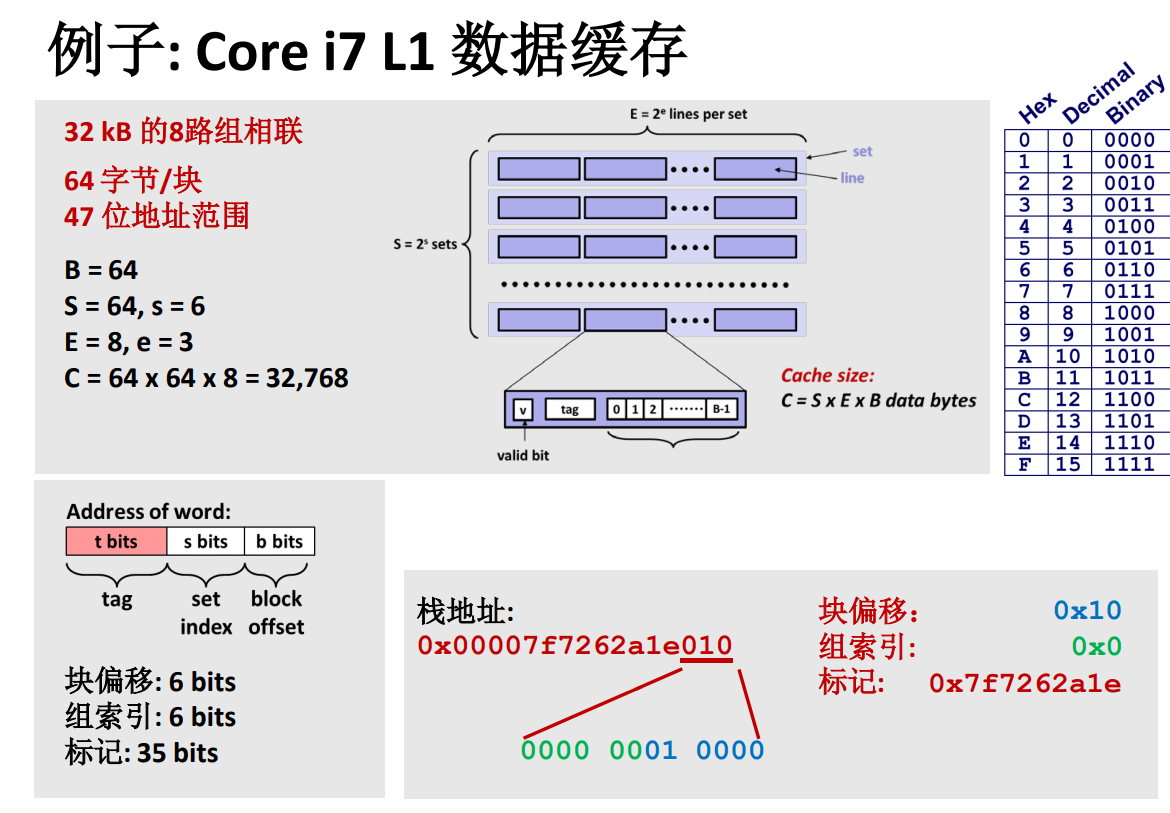
注意地址范围只用了 47 位!
性能指标
高速缓存中有许多指标用来衡量高速缓存是否高效运行,我们可以使用这些标准来衡量我们写的程序是否足够高效!


吞吐量
每秒钟从存储系统中读取 / 写入的字节数,单位是 \(MB/s\)。
存储器山
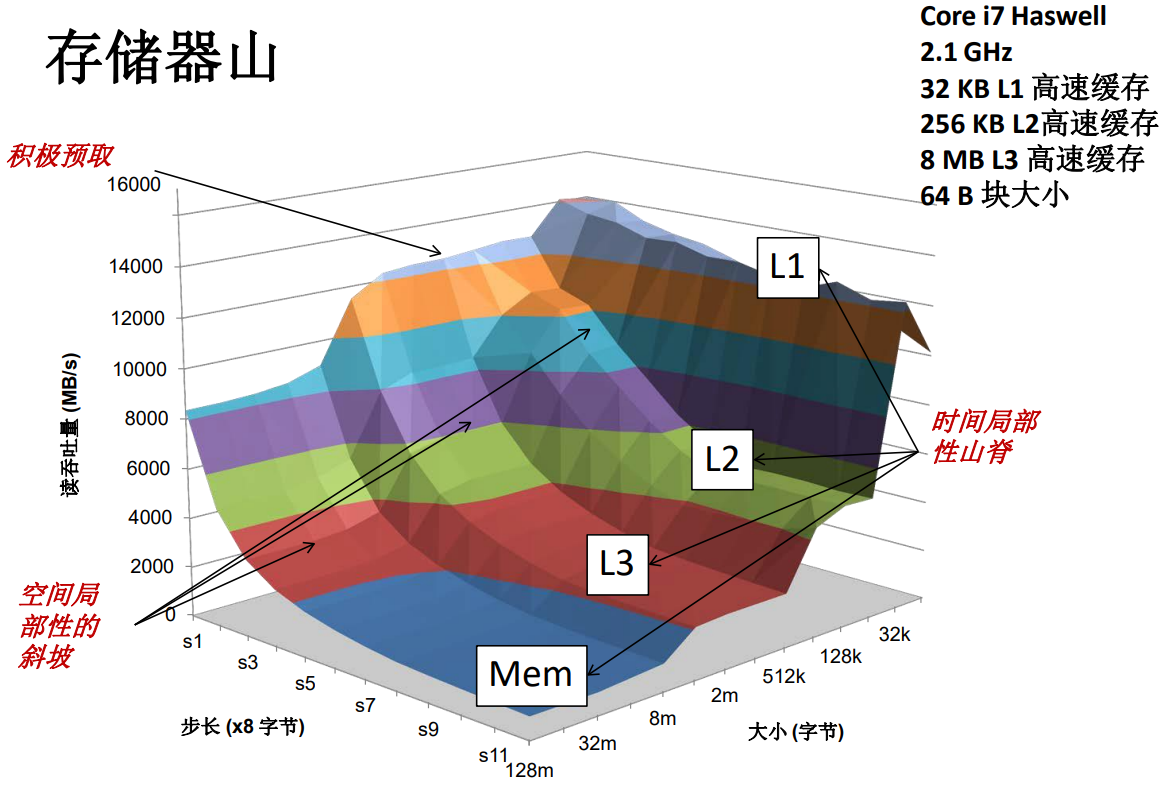
我们希望借助一个简单的程序来检验这个存储器山的特性。
存储器山测试函数
long data[MAXELEMS];
int test(int elems, int stride) {
long i, sx2=stride*2, sx3=stride*3, sx4=stride*4;
long acc0 = 0, acc1 = 0, acc2 = 0, acc3 = 0;
long length = elems, limit = length - sx4;
/* Combine 4 elements at a time */
for (i = 0; i < limit; i += sx4) {
acc0 = acc0 + data[i];
acc1 = acc1 + data[i+stride];
acc2 = acc2 + data[i+sx2];
acc3 = acc3 + data[i+sx3];
}
for(; i<length; i++) {
acc0 = acc0 + data[i];
}
return ((acc0 + acc1) + (acc2 + acc3));
}
矩阵乘法的例子

这个例子使用的算法就是最朴素的矩阵乘法,左矩阵的行乘以右矩阵的列,然后将所有乘法的结果相加,得到 c 矩阵的一个元素。
矩阵不命中率分析
假设
- 块大小为 32 个字节 32Byte
- 矩阵的维数比较大
- 高速缓存的一个块不足以缓存矩阵的一整行元素
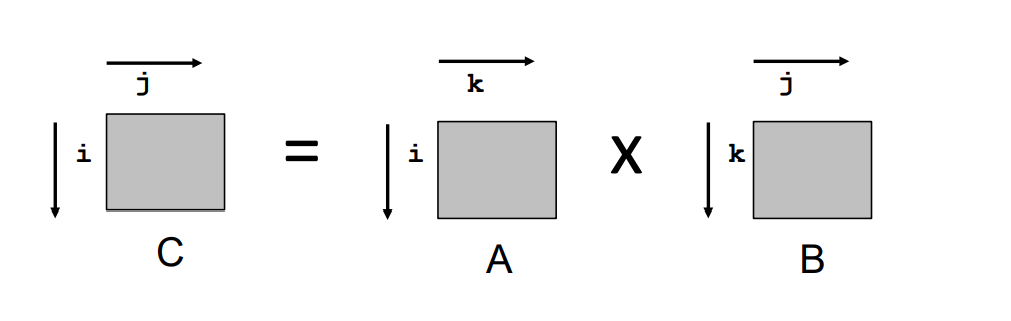
对于不同的内存访问方式,有着不一样的访问命中率,首先要明确的是内存对数组是按照行进行存储的,所以在行方向上存在命中的可能。

很显然,每一行的总大小远远大于高速缓存中一个缓存块的大小,因此缓存块一般来说是村放不下完整的一行的,因此按行扫描的时候命中率只有 \(1-(sizeof (a_{ij})/B)\),因此不命中率就是 \(sizeof (a_{ij})/B\),也就是说如果元素大小占了整个存储块的一半,那么它的不命中率就高大 \(50%\),因此可以看出当元素占的存储空间越小,高速缓存的命中率越高。
而按列扫描就不太可能命中,除了行很小,缓存块很大的情况。
矩阵乘法
此处的 \(ijk\) 代表了遍历顺序,也就是三个循环的顺序,最外层是 \(i\),次外层是 \(j\),最内层是 \(k\)。
ijk
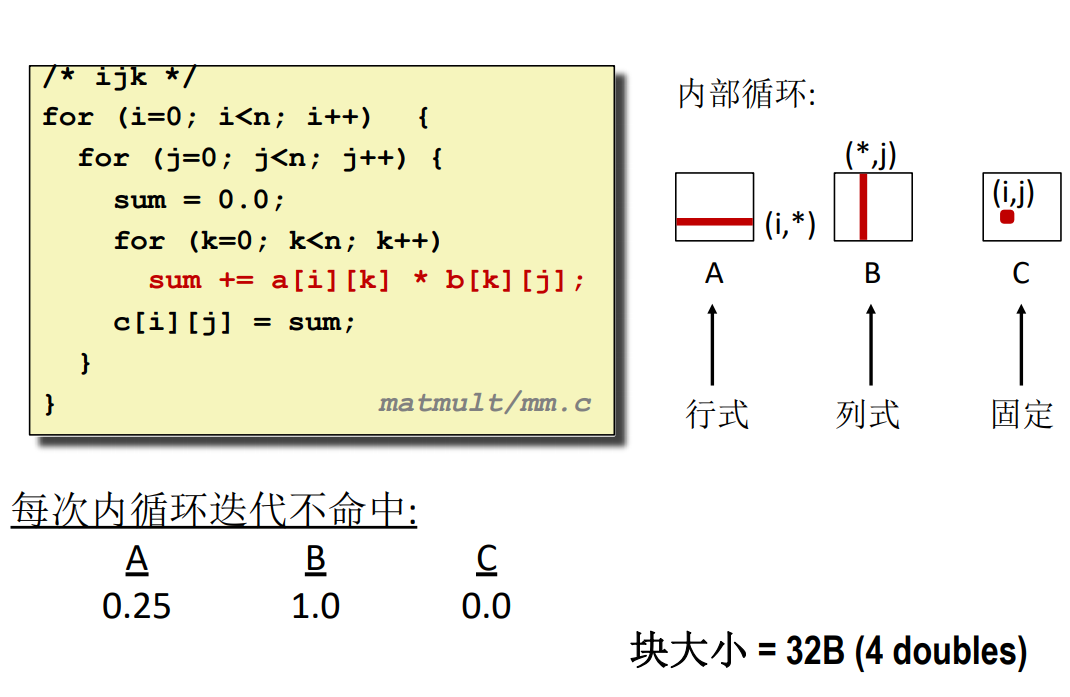
jik
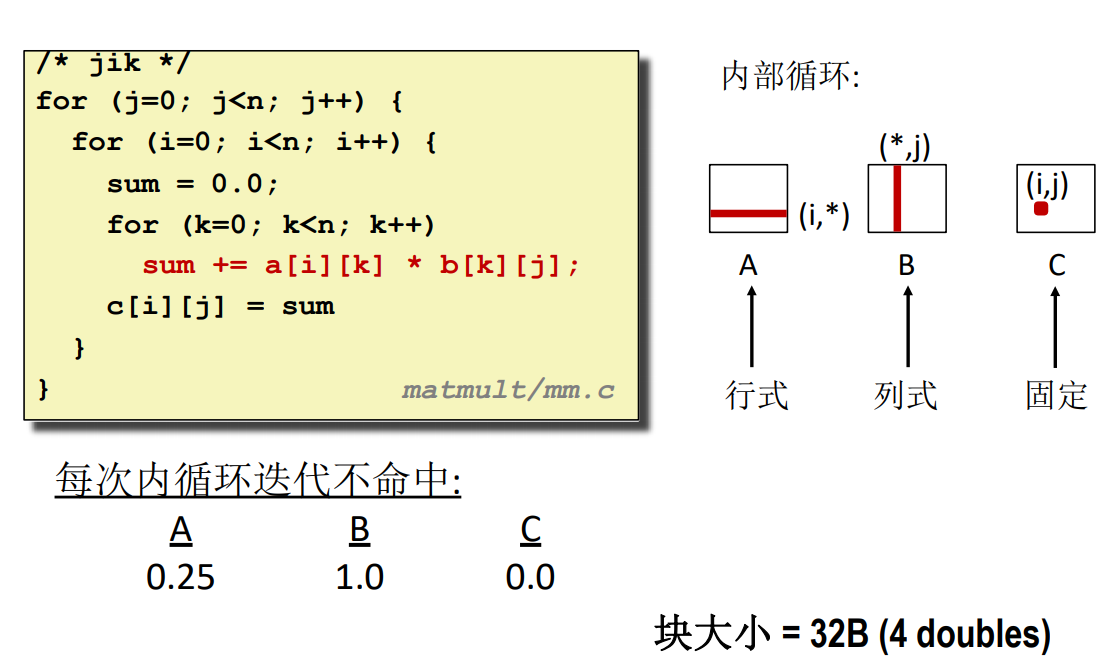
这种做法跟 ijk 的完全一致,对于 B 的访问都是按列访问,所以不命中率都是 \(1.0\)。
kij

这里的算法就完全是换了一个思路,并不直接使用矩阵乘法的定义,因为定义的算法中肯定会存在按列遍历,所以会有不命中率为 1 的情况,而这里把乘法结果矩阵的每一个元素拆成多个元素相加(虽然本来就是这样的,但这里的相加不是一次性加完,而是一行一行的加)
例如一个二阶方阵,它的左上角元素的表达式为 \(C[0][0]=A[0][0]*B[0][0]+A[0][1]*B[1][0]\),当使用上图的算法时,并不是一步算出来,而是通过两次 \(k\) 的循环,第一次让 \(C [0][0]=A[0][0]*B[0][0]\),第二次让 \(C[0][0]+A[0][1]*B[1][0]\),注意 \(k\) 的每次循环中,都有与 \(C [0][0]\) 相关的表达式,也就是说最外层的循环每经历一次,就会给 C 矩阵的所有位置加上一个数,而一共有 \(k\) 个乘法表达式,所以循环结束就是答案。
这里有一个共通之处是,所有的访问表达式都是:
因此可以作为一个记忆点。
ikj
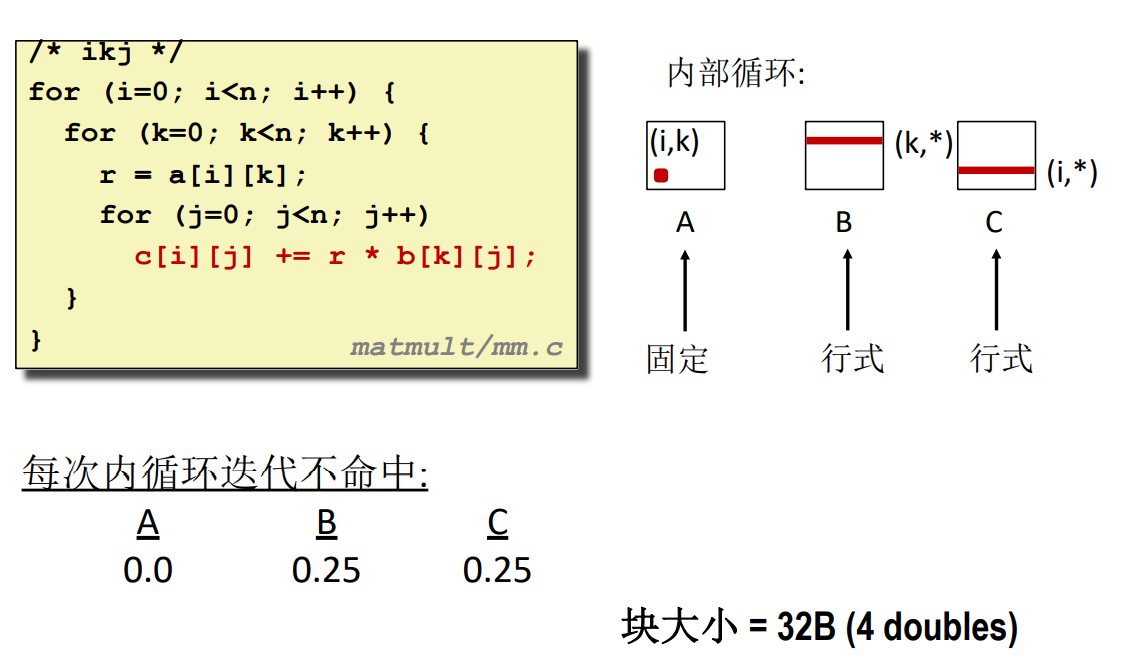
jki
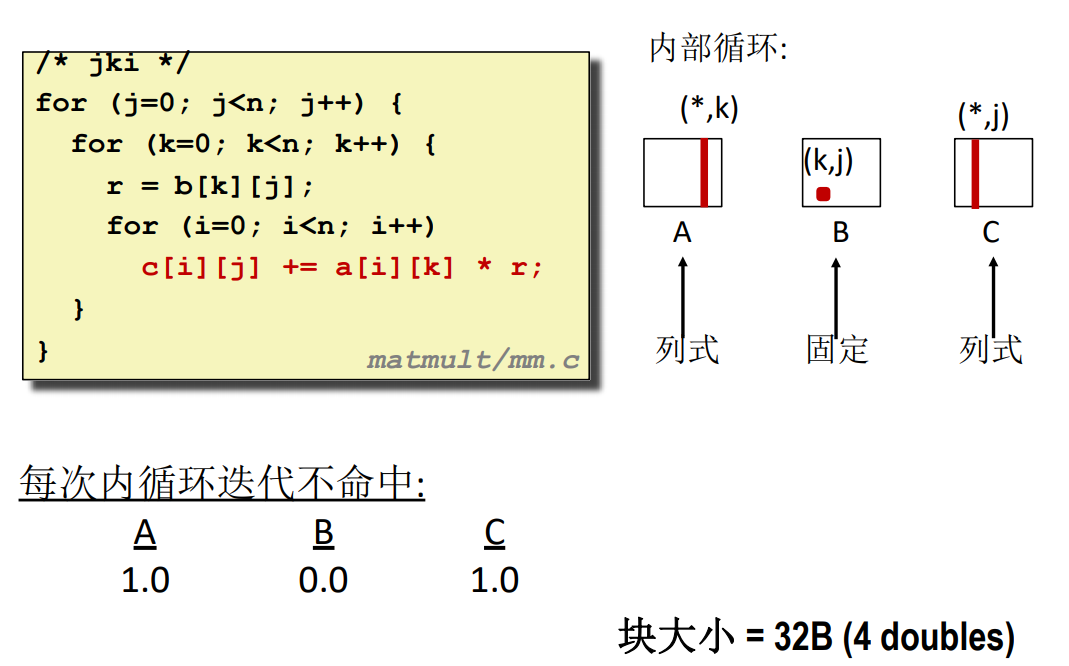
kji
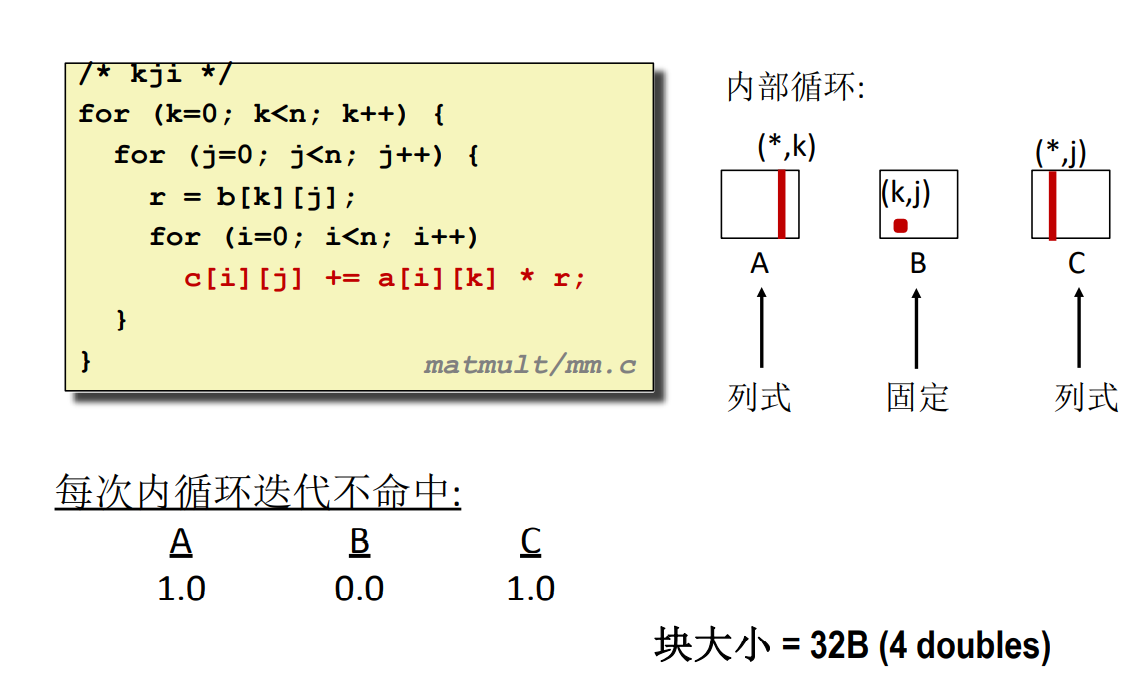
要看两个数相乘的结果是哪个元素的一部分可以通过 \((i,k) 和 (k,j)\) 的组合,将中间的 k 消去,得到的就是对应的元素位置 \((i,j)\)。只要满足这个表达式,不管怎么乘,什么时候加都是可以的。不同算法实际上就是调整位置而已。
矩阵乘法总结

性能差异
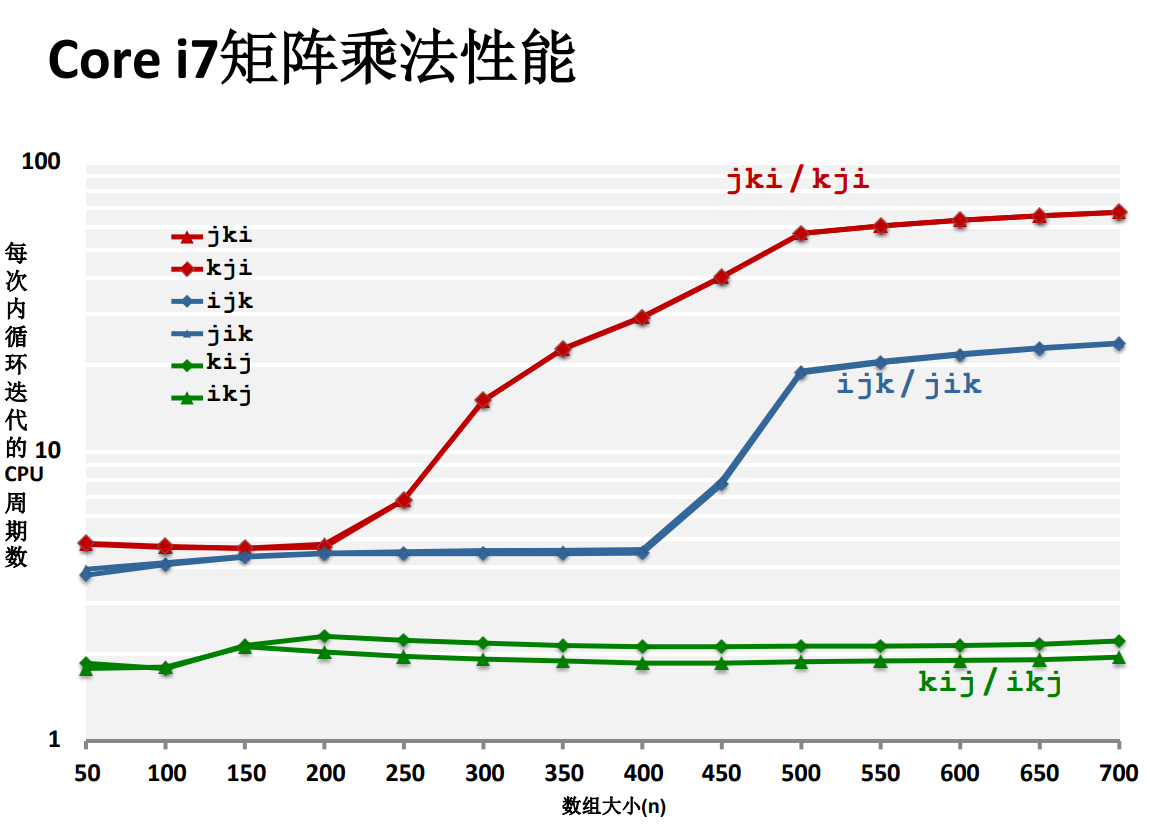
不命中率的理论分析
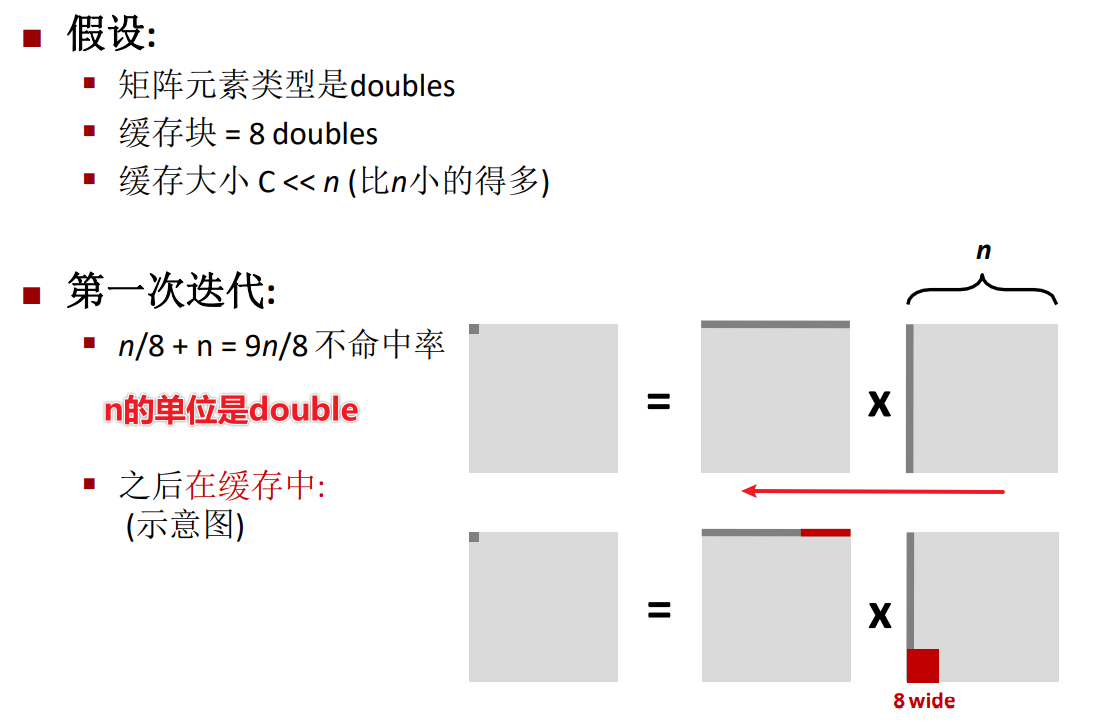
这里等式两边交换了位置,\(\frac{n}{8}\)就是矩阵行的长度除以缓存块的长度,这里我的一个猜测是,每个元素的大小是1个double,那么一行有n个元素,而一个double元素的不命中率为\(\frac{1}{8}\),所以总的行不命中率就是\(\frac{n}{8}\)。
同样的,第二次迭代的不命中率也是\(\frac{9n}{8}\),因此最后总的不命中率为\(\frac{9n^3}{8}\)。
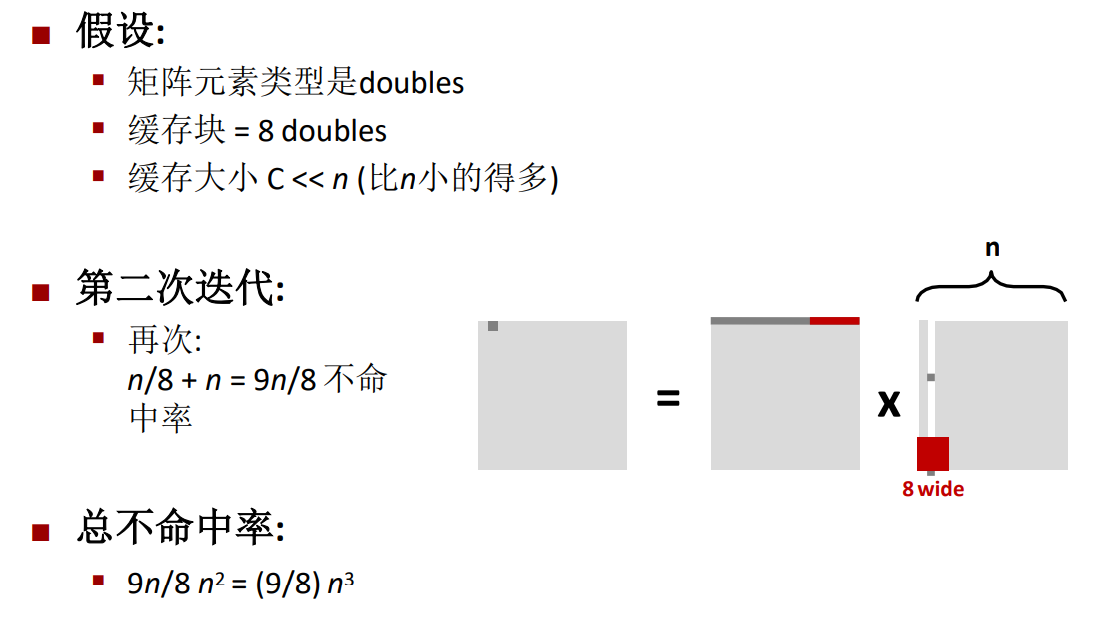
分块矩阵
c = (double *) calloc(sizeof(double), n*n);
/* Multiply n x n matrices a and b*/
void mmm(double *a, double *b, double *c, int n)
{
int i, j, k;
for (i = 0; i < n; i+=B)
for (j = 0; j < n; j+=B)
for (k = 0; k < n; k+=B) /* B x B mini matrix multiplications */
for (i1 = i; i1 < i+B; i++)
for (j1 = j; j1 < j+B; j++)
for (k1 = k; k1 < k+B; k++)
c[i1*n+j1] += a[i1*n + k1]*b[k1*n + j1];
j1 c =i1 a * Block size B x B b + c;
}
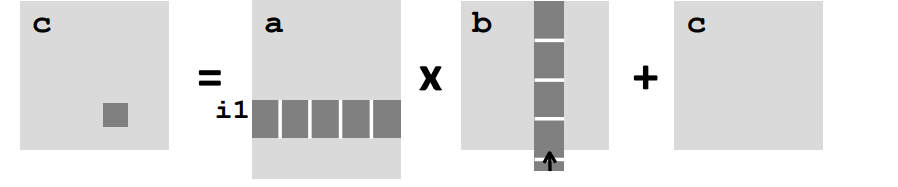
对此做出一定的假设,假设缓存块的大小是8 double,并且缓存的总大小远远小于矩阵的行数,但是满足约束条件\(3B^2<C\),也就是说最少可以放入三个分块矩阵。
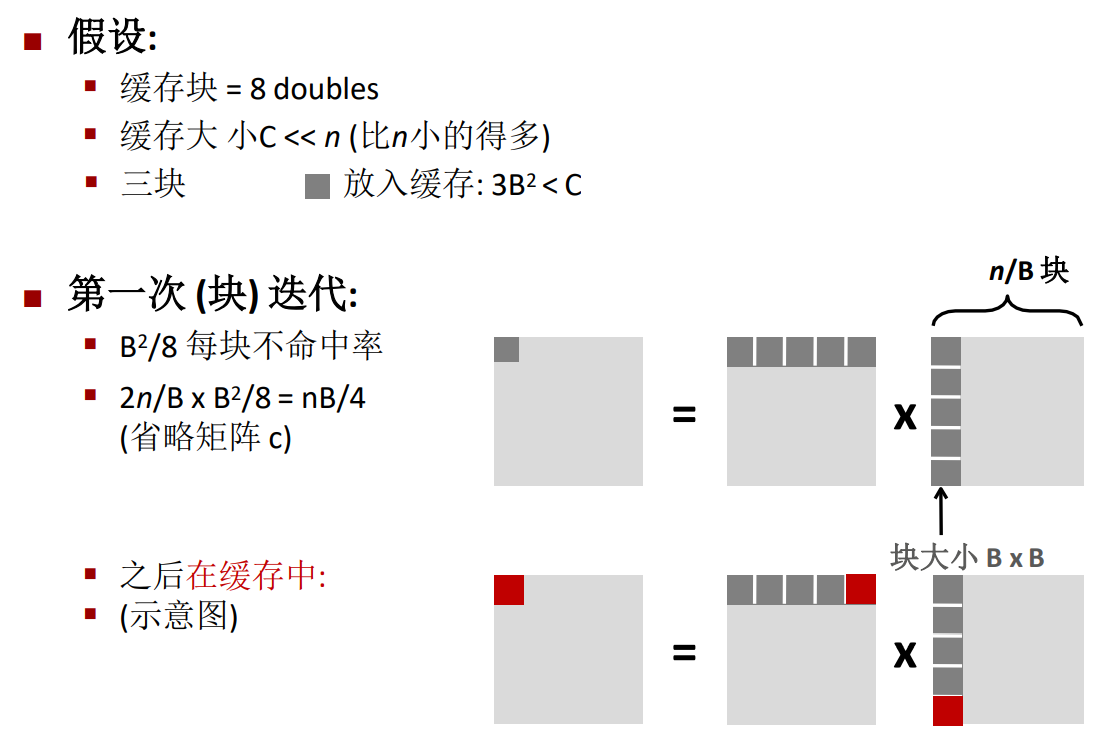
其中的\(\frac{2n}{B}\)代表每次运算的时候有这么多的分块矩阵参与运算,矩阵数量乘以每块矩阵的不命中率,得到的就是第一次迭代的总的不命中率。
第二次迭代也是一样。
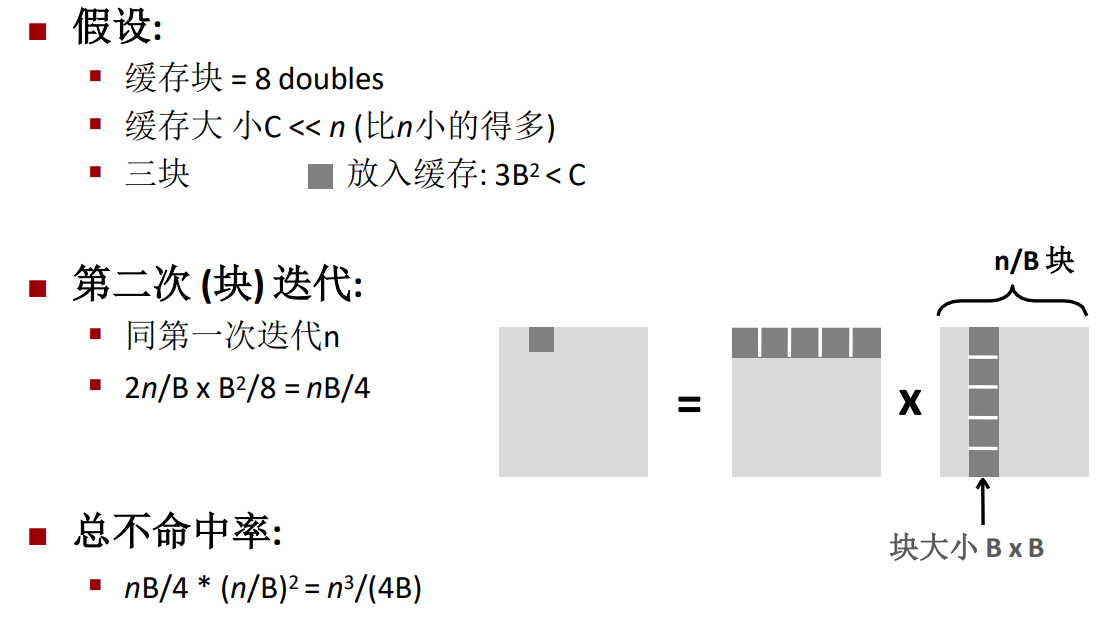
最后可以得到
-
不分块的情况下,不命中率是\(\frac{9n^3}{8}\)。
-
分块的情况下是\(\frac{n^3}{4B}\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号