平面解析几何
一、平面直角坐标系
-
平面直角坐标系

-
点P的坐标(a,b)
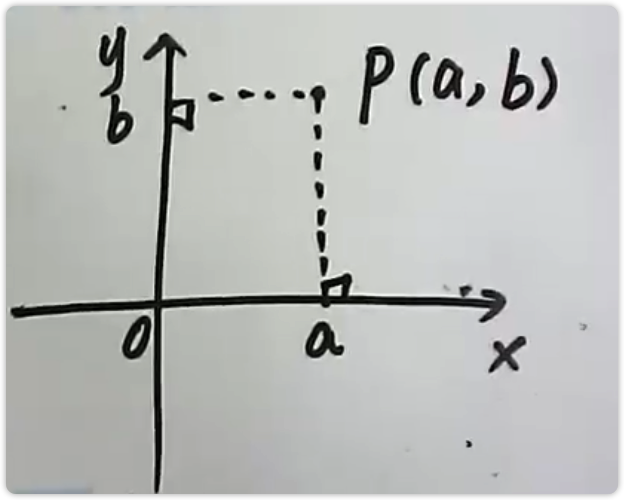
-
象限

二、直线
-
斜截式方程:
y = kx+b (k为斜率)- 作用:找斜率
- y在左,且系数为1,x与常数在右,x的系数为斜率
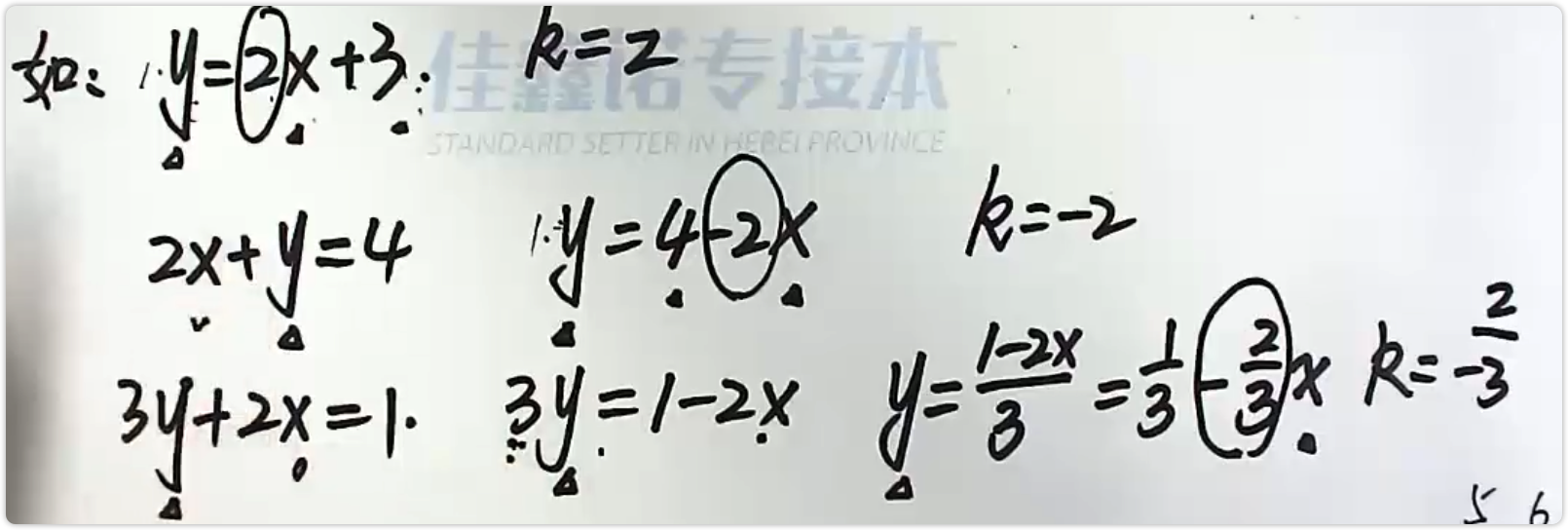
-
已知直线上两点M1(x1,y1)M2(x2,y2),则直线斜率:
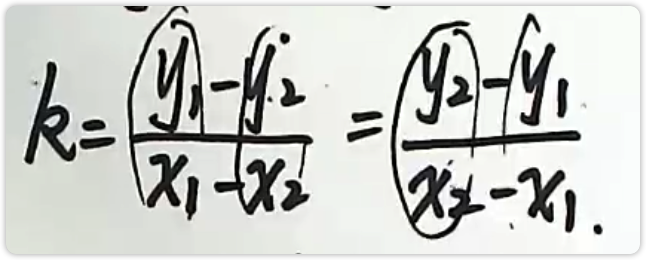
纵坐标之差比上对应的横坐标之差。


-
点斜式方程(求直线方程):直线L过点M0(x0,y0),斜率为k,则直线L的方程:y-y0 = k(x-x0)
(整理成斜截式方程)
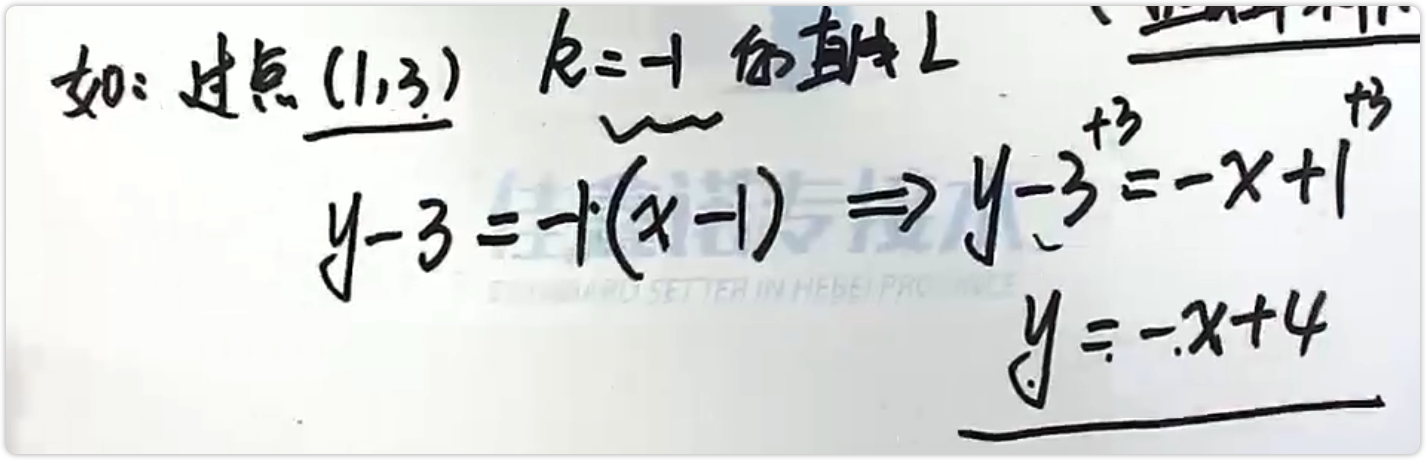

-
直线L1:y=k1x+b1 ,直线L2:y=k2x+b2 ,两直线平行(L1//L2) <==> k1 = k2 , 两直线垂直(L1⊥L2) <==> k1 · k2 = -1


-
画直线的图像(描两个点),
y=kx+b令y=0,x = ?,x=0,y=?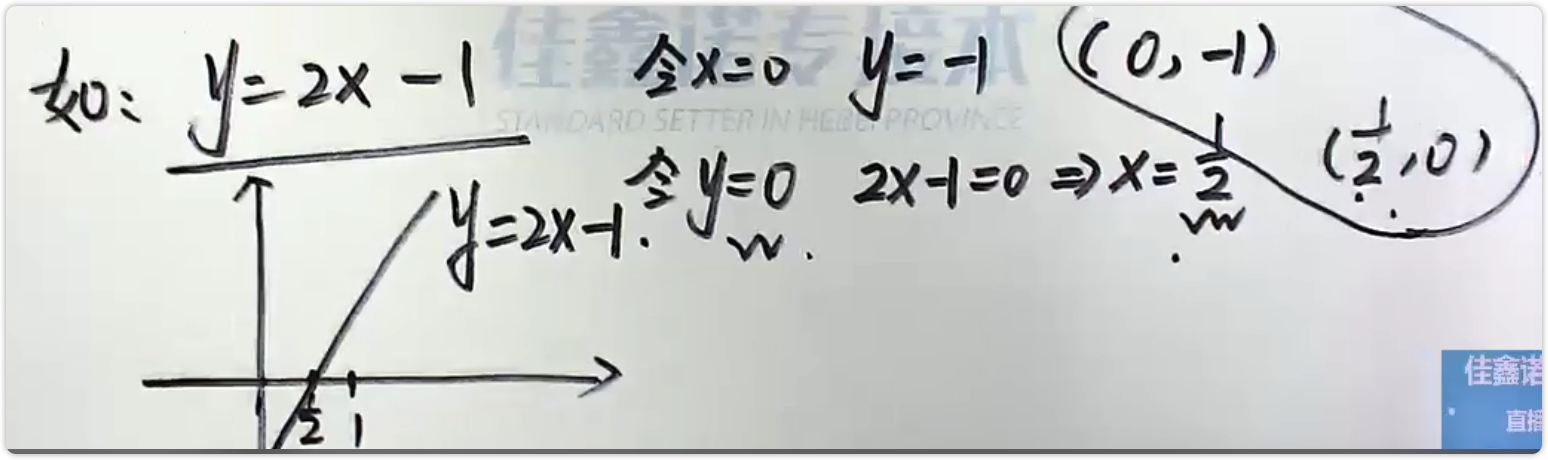
特殊的:y = c 为一条水平线;x = c 为一条垂直线
二、抛物线
-
形如y=ax2+bx+c (a≠0) 的方程为一条抛物线,开口上下。
画图流程:
- 确定开口方向:
- a>0 开口向上
- a<0 开口向下
- 确定与x轴的交点
- 令y=0,ax2+bx+c = 0,根为与x轴的交点横坐标
- 确定与y轴的交点
- 令x=0,y=c ,(0,c)为与y轴的交点
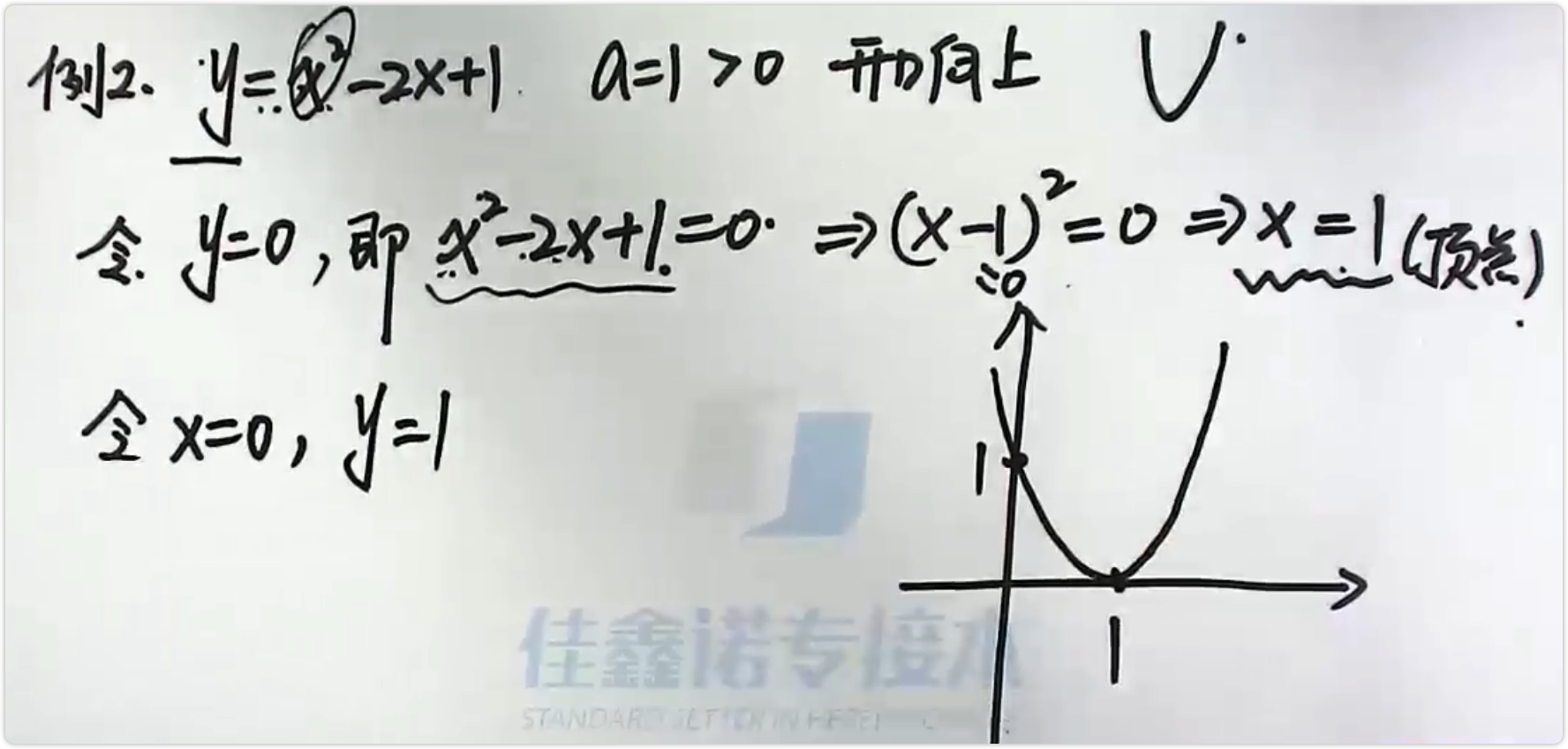
- 确定开口方向:
-
形如x=ay2+by+c (a≠0) 的方程为一条抛物线,开口左右。
画图流程:
- 确定开口方向:
- a>0 开口向右
- a<0 开口向左
- 确定与y轴的交点
- 令x=0,ay2+yx+c = 0,根为与y轴的交点纵坐标
- 确定与x轴的交点
- 令y=0,x=c ,(c,0)为与x轴的交点
- 确定开口方向:
-
求交点坐标
联立方程,求方程组的解,即交点坐标。




