树状数组整理

• 一直觉得树状数组是个非常神奇的东西，代码不知道要比线段树短多少倍，还有什么 \(lowbit\) 之类的神奇操作。也是因此对其一直一知半解，用的时候都迷迷糊糊，瞎打一通。所以就写篇博客吧。。

---

树状数组：

本质上是一个动态的前缀和，可以 \(O(logn)\) 维护单点修改， \(O(logn)\) 求一个前缀，预处理要 \(O(nlogn)\) 。

大体结构如图：

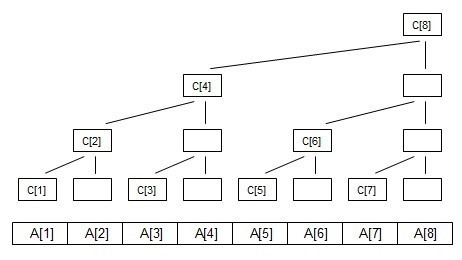
\(A[i]\) 数组表示原序列，\(C[i]\) 数组表示树状数组。

每次求和(更新)都是查询(改变)部分节点。( \(logn\) 个）

代码：

void Add(int x,int y){
	while(x<=n)c[x]+=y,x+=x&-x;
}
void Sum(int x){
	int res=0;
	while(x)res+=c[x],x-=x&-x;
	return res;
}

至于为什么是 \(\pm x\&(-x)\) , 就不解释了我也不知道。

两种常见用法：

1. \(C[i]\) 表示前（后）缀

这是最常见的一种，也比较好理解，过一下就好了。

• Tips：如果表示后缀的话只用把 \(Add\) 和 \(Sum\) 里关于 \(x\) 的范围，正负号改一下就可以了。

• 单点更新，单点（一个前缀）查询。

例题：luogu P3374

#include<bits/stdc++.h>
using namespace std;
const int N=500005;
int a[N],c[N];
int n,m;
void Add(int x,int y){
	while(x<=n)c[x]+=y,x+=x&-x;
}
int Sum(int x){
	int res=1;
	while(x)res+=c[x],x-=x&-x;
	return res;
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		Add(i,a[i]);
	}
	int flag,x,y;
	while(m--){
		scanf("%d%d%d",&flag,&x,&y);
		if(flag==1)Add(x,y);
		else printf("%d\n",Sum(y)-Sum(x-1));
	}
	return 0;
}

2. \(C[i]\) 表示单点的值

这里存在一个差分数组的概念。

令 \(d[i]=a[i]-a[i-1]\)，则 \(a[k]=\Sigma_{i=1}^{k}{d[i]} (a[0]=0)\)

同样，如果是后缀的话正负号改一下。

因此就可以用前缀来表示某一个数了。

• 预处理：

scanf("%d%d",&n,&m);
int la=0;
for(int i=1,x;i<=n;i++){
    scanf("%d",&x);
    Add(i,x-la),la=x;
}

• \(Add\) 函数：

是更新后面整个序列（同时更新一堆数），如果要更新一段区间（或单点），也要用到差分的手法:

Add(x,k),Add(y+1,-k)

• \(Sum\) 函数：

这里的 \(Sum\) 不再是代表前缀或者后缀，而是表示单独的一个数。因此大多数情况只能单点查询，像luogu P3368 。如果想要实现区间查询也是可以的，比较复杂，要维护两个树状数组，这里暂时不做解释。