深(爆)搜专题整理
就要考CSP了,小C每天说要把暴力打满,然后就开了个爆搜专题。。
发现自己好久没打搜索了。。
问题 A: 汽车问题
有一个人在某个公共汽车站上,从12:00到12:59观察公共汽车到达本站的情况,该站被多条公共汽车线路所公用,他依次记下公共汽车到达本站的时刻。
-
在12:00-12:59期间,同一条线路上的公共汽车以相同的时间间隔到站。
-
时间单位用“分”表示,从0到59 。
-
每条公共汽车线路至少有两辆车到达本站。
-
公共汽车线路数K一定≤17,汽车数目N一定小于300。
-
来自不同线路的公共汽车可能在同一时刻到达本站。
-
不同公共汽车线路的车首次到站时间和到站的时间间隔都有可能相同。
请为公共汽车线路编一个调度表,目标是:公共汽车线路数目最少的情况下,使公共汽车到达本站的时刻满足输入数据的要求。
输入:
第一个整数n
接下来n个数字,表示每次到达的时间。
输出:
输出一个整数,表示最少的班次。
友情提示:看到的公交汽车线路一定是完整的:比如样例1中 0,3 是不符合要求的 而应该是 0,3,6,9... 直到最后看到的那辆车为止
先上代码:
#include<bits/stdc++.h>
#define debug(a) cout<<#a<<"="<<a<<endl
#define LL long long
using namespace std;
const int N=305;
int a[N],fir[N],len1,sec[N],len2,mark[N];
int ans,n;
void dfs(int x){
if(len1>=ans||len2>=ans)return;
if(x==n+1){
ans=min(ans,len1);
return;
}
if(mark[x]){dfs(x+1);return;}
fir[++len1]=x;
dfs(x+1);
len1--;
for(int i=1;i<=len1;i++){
if(mark[fir[i]])continue;
int r=a[x]-a[fir[i]];
int st=a[x];
for(int j=x;j<=n;j++)
if(!mark[j]&&a[j]==st)st+=r;
if(st<=a[n])continue;
mark[fir[i]]=1;
st=a[x];
for(int j=x;j<=n;j++)
if(!mark[j]&&a[j]==st)mark[j]=1,st+=r;
dfs(x+1);
mark[fir[i]]=0;
st=a[x];
for(int j=x;j<=n;j++)
if(mark[j]&&a[j]==st)mark[j]=0,st+=r;
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
ans=min((n+1)/2,17);dfs(1);
printf("%d\n",ans);
return 0;
}
- 思路:
刚看到这道题的时候,真不知道怎么写,连怎么搜都不知道。后来看了看题解发现,对于每条路径,可以记录这条路径的前两辆车,然后判断一下可行性,然后把这条路径剩下的车都标记掉。
于是就有了一个大题思路,用 \(fir[i]\) 记录第1辆车,\(sec[i]\) 记录第2辆车,\(mark[i]\) 记录编号为 \(i\) 的车是否已经在一条线路中。
- 剪枝:
- 由于题目保证可行,每条线路最少两辆车,所以 \(ans\) 最大大不过 \((n+1)/2\),在加上题目里说线路最多17条,所以 \(ans\) 的初始值为 \(min((n+1)/2,17)\) 。
- 最优性剪枝:比较显然,只要判断一下当前第一辆车的个数和 \(ans\) 的大小就好了。
-小问题:
写这道题的时候,对于如何判断这条线路是否可行卡了好久,总觉得一遍扫过来时间复杂度会太高,事实证明并没有什么关系。写都写了爆搜,时间复杂度都是 O(玄学) ,就别怕TLE了吧。。真不行还能优化。
问题B:奶牛求幂
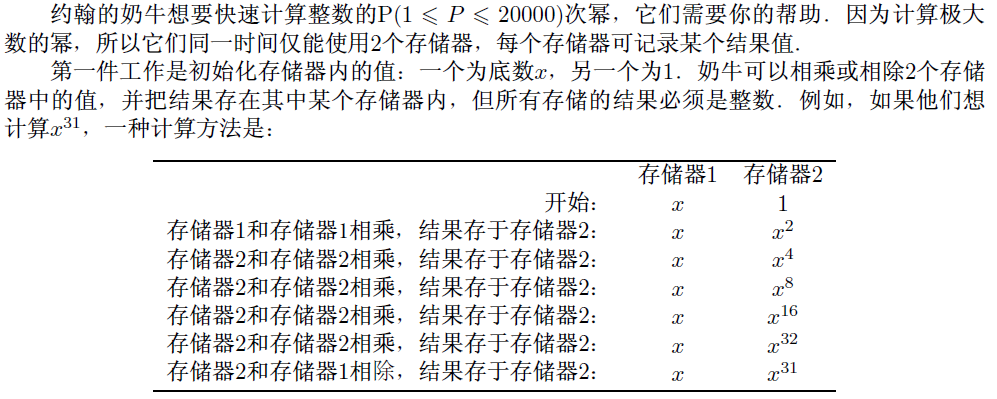
输入:一个整数P
输出:输出最少的计算次数
看起来好像是道结论题,但他就是爆搜。。。
对于最暴力的爆搜,有九分的好成绩。。就像这样:
#include<bits/stdc++.h>
using namespace std;
int ans=100,P;
void dfs(int x,int y,int step){
if(step>=ans)return;
if(x==P||y==P){ans=step;return;}
if(step+1>=ans)return;
if(x+y==P){ans=step+1;return;}
if(abs(x-y)==P){ans=step+1;return;}
if(x)
dfs(x,2*x,step+1);
dfs(2*x,y,step+1);
}
if(y){
dfs(2*y,y,step+1);
dfs(x,2*y,step+1);
}
if(x>=y){
dfs(x-y,y,step+1);
dfs(x,x-y,step+1);
}
if(x<=y){
dfs(x,y-x,step+1);
dfs(y-x,y,step+1);
}
}
int main(){
scanf("%d",&P);dfs(1,0,0);
printf("%d\n",ans);
return 0;
}
可以看出,这样搜索每次的分支极多,搜索树极其可怕,T到飞起。
这道题的答案其实不是很大,之所以会T,主要是在一些非最优解情况上越走越远,永不回头。
于是就有了一种搜索的套路:迭代加深(??)
其实就是从小到大枚举步数,然后看一下在当前步数里能不能得到答案。这样不仅可以避免个别分支太深的情况,还方便剪枝。
代码:
#include<bits/stdc++.h>
using namespace std;
int P,K,f2[25];
int gcd(int x,int y){return y==0?x:gcd(y,x%y);}
bool dfsid(int x,int y,int step){
if(step>=K){
if(x==P||y==P)return 1;
return 0;
}
if(x&&y&&P%gcd(x,y))return 0;
int nw=max(x,y);
if(1ll*nw*f2[K-step]<P)return 0;
if(dfsid(x,2*x,step+1))return 1;
if(dfsid(2*x,y,step+1))return 1;
if(dfsid(2*y,y,step+1))return 1;
if(dfsid(x,2*y,step+1))return 1;
if(dfsid(x,x+y,step+1))return 1;
if(dfsid(x+y,y,step+1))return 1;
if(dfsid(abs(x-y),y,step+1))return 1;
if(dfsid(x,abs(x-y),step+1))return 1;
return 0;
}
int main(){
scanf("%d",&P);
f2[0]=1;
for(int i=1;i<=24;i++)f2[i]=f2[i-1]*2;
K=0;
while(1){
if(dfsid(1,0,0)){
printf("%d\n",K);
return 0;
}
K++;
}
return 0;
}
代码里的剪枝大概看一下就好了,主要是方法。
问题 D: 邮票面值设计
这在luogu上居然是道绿题?? 怎么也得有个蓝题吧。
正解:搜索+DP
从小到大枚举要选的邮票面值,\(dfs\) 里传当前选了几个数以及前多少个数都能被表示出来。每次枚举当前数时用DP来求选了这个数之后前多少个数能被表示出来。
具体枚举的上下界等可以看代码:
#include<bits/stdc++.h>
using namespace std;
const int N=20,inf=1e9;
int a[N],ans[N],dp[300005];
int Mx,n,K;
int DP(int x){
dp[0]=0;
for(int i=1;i<=a[x]*n;i++)dp[i]=inf;
for(int i=1;i<=x;i++)
for(int j=a[i];j<=a[x]*n;j++)
dp[j]=min(dp[j],dp[j-a[i]]+1);
for(int i=1;i<=a[x]*n;i++)
if(dp[i]>n)return i-1;
return a[x]*n;
}
void dfs(int x,int mx){
if(x>K){
if(mx>Mx){
Mx=mx;
for(int i=1;i<=n;i++)ans[i]=a[i];
}
return;
}
for(int i=a[x-1]+1;i<=mx+1;i++){
a[x]=i;
dfs(x+1,DP(x));
}
}
int main(){
scanf("%d%d",&n,&K);
dfs(1,0);
for(int i=1;i<=K;i++)printf("%d ",ans[i]);
printf("\nMAX=%d\n",Mx);
return 0;
}
看起来时间复杂度挺高的,但就是能过
这三道题比较有意思,其他的就是能不能想到剪枝的问题了。
考试的时候还是不怎么敢打搜索,总感觉会有更好的方法,像dp什么的。其实有的时候,搜索加剪枝跑地还是很快的。虽然dp更快
整数分解:
给定正整数 \(n\) 和 \(k\) ,问能否将 \(n\) 分解为 \(k\) 个不同正整数的乘积。
多组测试数据。
\(T<=4000,n<=1e9,k<=17\)
虽然一看就像是搜索,但是考试时的我还是打了个玄学dp,跑的是很快,但是被卡内存了,只有50分。考后看见别人十几行搜索代码AC???,贪心代码水到80分???
代码:
namespace P2{
bool dfs(int n,int nw,int cnt){
if(cnt>=K)return 1;
while(nw*nw<=n&&n%nw)nw++;
if(nw*nw>=n)return cnt+(n>=nw)>=K;
LL Mi=1;
for(int i=0;i<=K-cnt-1;i++)Mi*=(nw+i);
if(n<Mi)return 0;
if(dfs(n/nw,nw+1,cnt+1))return 1;
if(dfs(n,nw+1,cnt))return 1;
return 0;
}
void solve(){
if(dfs(n,2,1))puts("TAK");
else puts("NIE");
}
}

具体就是剪枝的问题。


