给定二维平面整数点集输出“最大点集”算法(今日头条面试题)
引子
最近自己的独立游戏上线了,算是了却了一桩心愿。接下来还是想找一份工作继续干,创业的事有缘再说。
找工作之前,总是要浏览一些实战题目,热热身嘛。通过搜索引擎,搜到了今日头条的一道面试题。
题目
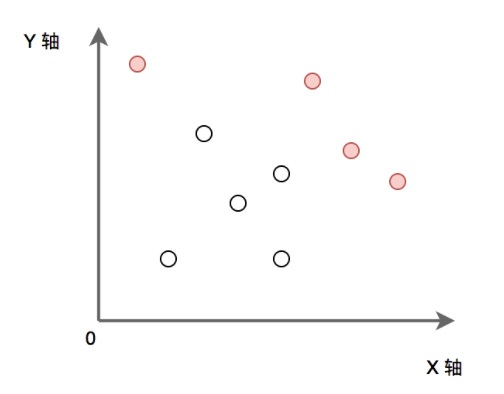
P为给定的二维平面整数点集。定义 P 中某点x,如果x满足 P 中任意点都不在 x 的右上方区域内(横纵坐标都大于x),则称其为“最大的”。求出所有“最大的”点的集合。(所有点的横坐标和纵坐标都不重复, 坐标轴范围在[0, 1e9) 内)
如下图:实心点为满足条件的点的集合。请实现代码找到集合 P 中的所有 ”最大“ 点的集合并输出。
输入描述:
第一行输入点集的个数 N, 接下来 N 行,每行两个数字代表点的 X 轴和 Y 轴。
输出描述:
输出“最大的” 点集合, 按照 X 轴从小到大的方式输出,每行两个数字分别代表点的 X 轴和 Y轴。
输入例子1:
5 1 2 5 3 4 6 7 5 9 0
输出例子1:
4 6 7 5 9 0
思路
1.暴力搜索法
先取一点,然后和其他所有点比较,看看是否有点在其右上方,没有则证明该点是“最大点”。重复检测所有的点。显而易见,算法的复杂度为O(n2)
2.变治法(预排序)
由“最大点”的性质可知,对于每一个“最大点”,若存在其他点的y值大于该点y值,那么其他点x值必然小于该点的x值。
换言之,当某一点确定它的x值高于所有y值大于它的点的x值,那么该点就是“最大点” 。网上给出的答案基本上都是这个套路。
对于y有序的点集,只需要O(n)即可输出“最大点”点集。一般基于比较的排序算法时间复杂度O(nlogn)。那么,显而易见,算法整体复杂度为O(nlogn)。
3.减治法+变治法(过滤+预排序)
过滤很简单,就是在集合中找出一个比较好的点,然后过滤掉其左下角的所有点。然后再采用方法2对过滤后的点集求解。
那么这个集合中比较好的点,怎么找,或者说哪个点是比较好的点。显而易见,越靠近点集右上角的点,左下角的面积就越大,越可以过滤更多的点,故越好。
儿时学过,两个数的和一定,那么两数差越小,乘积越大。简单设计,该点x和y的和减去x和y差的绝对值越大,该点越好。
4.空间分割(优化的四叉树)
因为之前对四叉树有一定的了解,所以对于这个问题也想到能不能有四叉树去处理。如果有同学熟悉KD树思路大致是一样。 为了优化将点集插入到四叉树的时间,笔者使用预先开辟数组来表示四叉树。对于500000个点,大概所需时间如下:
build tree cost: 167ms 105233923 999996852 398502327 999994996 837309014 999994263 899779160 999993102 980746971 999976098 990941053 999881685 991773349 999539486 996437667 999536388 999934209 999456481 999948454 989946068 999951793 933115039 999993165 920862637 999996248 471725091 search tree cost: 106ms
假设点集数量为n,构建n次矩形查询,第i次查询范围为以第i个点为左下角以数据最大范围为右上角的矩形,若该点右上方没有点那么该点为“最大点”。若该点为“最大点”,我们还可以以它为右上角,以0点位左下角构建范围查询,过滤哪些不需要查询的点。通过对比可知,查询时间可以接受,但构建时间确实长了一些。可能导致该方法还没有直接预排序好。总体时间复杂度应该也是O(nlogn)级别,大部分时间都用于构建了,构建时涉及到的内存操作比较多必然消耗更多时间。本来没有使用预排序就可以获取结果,我们的输出结果可以匹配输入顺序,牛客网的答案要求以x从小到大排序,故结果还要重新排序。。。如果结果集非常大,对结果集排序会消耗大量时间。很可惜,四叉树无法通过测试,一是C#的输入输出会占用大量时间,二是我们还需要对结果集重新排序。但实验证明了对于随机500000点,使用四叉树可以和预排序有着差不多的时间复杂度。最后,还有交代一个重要问题:
int x=999999991; float y = 1000000000f; float z = x/y;
请问z值为何?答案是1.0f,因为float的精度不足,无法表示0.999999991,所以变成了1.0f,这个问题一度使我的四叉树以为小概率出现异常。找了半天才揪出来。
附上代码,备忘。
using System.IO; using System; using System.Collections.Generic; using System.Diagnostics; class Program { private static int maxData = 1000000000; private static List<MyPoint> dataPoints = new List<MyPoint>(); private static Random rand = new Random(); static void Main() { float time = 0; Stopwatch watch = new Stopwatch(); watch.Start(); Quadtree quad = new Quadtree(5, new Rectangle(0, 0, maxData, maxData)); int count = int.Parse(Console.ReadLine()); for (int i = 0; i < count; i++) { MyPoint temp; //string[] inputs = Console.ReadLine().Split(new char[] { ' ' }); //temp.x = Convert.ToInt32(inputs[0]); //temp.y = Convert.ToInt32(inputs[1]); temp.x = rand.Next(maxData); temp.y = rand.Next(maxData); dataPoints.Add(temp); quad.Insert(temp); } time = watch.ElapsedMilliseconds - time; Console.WriteLine("build tree cost: " + time + "ms"); List<MyPoint> result = new List<MyPoint>(); Rectangle rect; rect.width = rect.height = maxData + 1; for (int i = 0; i < count; i++) { rect.x = dataPoints[i].x; rect.y = dataPoints[i].y; if (quad.retrieve(rect)) { continue; } result.Add(dataPoints[i]); } //要以x轴y从小到大输出,所以结果集需要排序 result.Sort(); for(int i=0;i< result.Count; i++) { Console.WriteLine( result[i]); } time = watch.ElapsedMilliseconds - time; Console.WriteLine("search tree cost: " + time + "ms"); watch.Stop(); } } public class Quadtree { private class QuadtreeData { public int maxLevel; public double maxWidth; public double maxHeight; public Quadtree[] allNodes; public QuadtreeData(int maxLevel,float maxWidth,float maxHeight) { this.maxLevel = maxLevel; this.maxWidth = maxWidth; this.maxHeight = maxHeight; int maxNodes = 0; for (int i = 0; i <= maxLevel; i++) { maxNodes += (int)Math.Pow(4, i); } allNodes = new Quadtree[maxNodes]; } } private int level; private int parent; private int count; private List<MyPoint> points; private Rectangle bounds; private Quadtree[] nodes; private QuadtreeData data; public Quadtree(int maxLevel,Rectangle bounds) { data = new QuadtreeData(maxLevel,bounds.width,bounds.height); this.bounds = bounds; level = 0; count = 0; parent = -1; nodes = new Quadtree[4]; Init(); } private void Init() { data.allNodes[0] = this; for (int i = 0; i < data.allNodes.Length; i++) { if (data.allNodes[i].level >= data.maxLevel) break; InitChildrenNew(i); } } private void InitChildrenNew(int parentIndex) { Rectangle bounds = data.allNodes[parentIndex].bounds; float subWidth = (bounds.getWidth() / 2); float subHeight = (bounds.getHeight() / 2); float x = bounds.getX(); float y = bounds.getY(); int nextLevel = data.allNodes[parentIndex].level + 1; byte[,] offset =new byte[,]{{0,0},{1,0},{0,1},{1,1}}; for (int i = 0; i < 4; i++) { Rectangle rect = new Rectangle(x,y,subWidth,subHeight); rect.x += offset[i,0]*subWidth; rect.y += offset[i,1]*subHeight; int childIndex = GetPointIndexByLevel(rect.getCenter(), nextLevel); if (childIndex < data.allNodes.Length) { data.allNodes[childIndex] = new Quadtree(nextLevel, rect, data); data.allNodes[childIndex].parent = parentIndex; data.allNodes[parentIndex].nodes[i] = data.allNodes[childIndex]; //Console.WriteLine("p:"+parentIndex+",c:"+childIndex+",size:"+ rect.width); } } } private Quadtree(int pLevel, Rectangle pBounds , QuadtreeData pData) { level = pLevel; bounds = pBounds; nodes = new Quadtree[4]; count = 0; data = pData; } public int GetPointIndexByLevel(MyPoint point, int targetLevel) { int[] indexByLevel={0,1,5,21,85,341,1365,5461,21845}; int startIndex =indexByLevel[targetLevel] ; int cc = (int)Math.Pow(2, targetLevel); //if(point.x >= data.maxWidth || point.y >=data.maxHeight) //{ // Console.WriteLine("error point:"+point); // Console.WriteLine("data:"+data.maxWidth+","+data.maxHeight); //} int locationX = (int)(point.x / data.maxWidth * cc); int locationY = (int)(point.y / data.maxHeight * cc); int idx = startIndex + locationY * cc + locationX; return idx; } /* * Insert the object into the quadtree. If the node * exceeds the capacity, it will split and add all * objects to their corresponding nodes. */ public void Insert(MyPoint point) { int idx = GetPointIndexByLevel(point, data.maxLevel); var nodeToAdd = data.allNodes[idx]; if (nodeToAdd != null) { if (nodeToAdd.points == null) nodeToAdd.points = new List<MyPoint>(); nodeToAdd.points.Add(point); nodeToAdd.AddCount(); } } private void AddCount() { if(parent >=0 ) { var nodeParent = data.allNodes[parent]; nodeParent.AddCount(); } count++; } /* * Return all objects that could collide with the given object */ public bool retrieve(Rectangle pRect) { if(count > 0 && pRect.Contains(bounds)) { return true; } if(count > 0 && bounds.Intersects(pRect)) { if (points != null) { for (int i = 0; i < points.Count; i++) { if (pRect.Contains(points[i])) { return true; } } } else if (level < data.maxLevel) { if (nodes[3] != null && nodes[3].retrieve(pRect)) return true; if (nodes[2] != null && nodes[2].retrieve(pRect)) return true; if (nodes[1] != null && nodes[1].retrieve(pRect)) return true; if (nodes[0] != null && nodes[0].retrieve(pRect)) return true; } } return false; } } public struct MyPoint : IComparable<MyPoint> { public int x; public int y; public MyPoint(int x = 0, int y = 0) { this.x = x; this.y = y; } public override string ToString() { return x + " " + y; } public int CompareTo(MyPoint other) { if(x == other.x) return 0; else if(x > other.x) return 1; else if( x < other.x) return -1; return -1; } } public struct Rectangle { public float x; public float y; public float height; public float width; public Rectangle(float x = 0, float y = 0, float width = 0, float height = 0) { this.x = x; this.y = y; this.width = width; this.height = height; } public float getX() { return x; } public float getY() { return y; } public float getHeight() { return height; } public float getWidth() { return width; } public MyPoint getCenter() { return new MyPoint((int)(x + width / 2), (int)(y + height / 2)); } public bool Intersects(Rectangle Rect) { return (!(y > Rect.y + Rect.height || y + height < Rect.y || x + width < Rect.x || x > Rect.x + Rect.width)); } public bool Contains(MyPoint point) { return (x < point.x && x + width >= point.x && y < point.y && y + height >= point.y); } public bool Contains(Rectangle other) { return Contains(new MyPoint((int)other.x,(int)other.y)) && Contains(new MyPoint((int)(other.x+other.width),(int)(other.y+other.height))); } public override string ToString() { return "Rect:" + x + "," + y + "," + width; } }
过滤与直接预排序对比实现
#include<iostream> #include<algorithm> #include<vector> #include <cstdlib> #include <ctime> using namespace std; struct point{ //定义结构体 int x,y; }; bool cmp(point a,point b){ //自定义排序方法 return a.y==b.y?a.x>b.x:a.y<b.y; //y升序,x降序 } int main(){ clock_t start,finish; double totaltime; std::srand(std::time(nullptr)); // use current time as seed for random generator int count; cout<<"输入点的个数和点:" ; cin>>count;
cout<<"输入总点数为:"<<count<<endl; vector<point> p; //容器用来装平面上的点 for(int i=0;i<count;i++){ point temp; temp.x = std::rand()% 100000000; temp.y = std::rand()% 100000000; p.push_back(temp); //为了方便对比性能,我们随机插入大量点 }
cout<<"------------------过滤后再使用预排序:------------------------------"<<endl; start = clock(); vector<point> filter;//定义过滤容器 vector<point> res; //定义结果容器 int curMaxRank = 0; int curMaxIndex = 0; for(int i=0;i<count;i++){ int temp =p[i].x+p[i].y-std::abs(p[i].x-p[i].y); if(temp > curMaxRank) { curMaxRank = temp; curMaxIndex = i; } } for(int i=0;i<count;i++) { if(p[i].x >= p[curMaxIndex].x || p[i].y>= p[curMaxIndex].y) { filter.push_back(p[i]); } } sort(filter.begin(),filter.end(),cmp); res.push_back(filter[filter.size()-1]); //左上角的那个点,一定符合条件 int maxx=filter[filter.size()-1].x; for(int i=filter.size()-2;i>=0;i--){ //y从大到小,若i点x值大于所有比其y值大的点的x值,那么i点为“最大点”。 if(filter[i].x>maxx){ res.push_back(filter[i]); maxx=filter[i].x; } } finish = clock(); cout<<"过滤后点数量:"<<filter.size()<<endl; cout<<"符合条件的点数量:"<<res.size()<<endl; for(int i=0;i<res.size();i++){ printf("%d %d\n", res[i].x, res[i].y); } totaltime=(double)(finish-start)/CLOCKS_PER_SEC; cout<<"\n此程序的运行时间为"<<totaltime<<"秒!"<<endl; cout<<"------------------直接使用预排序:------------------------------"<<endl; start = clock(); sort(p.begin(),p.end(),cmp); res.clear(); res.push_back(p[p.size()-1]); //左上角的那个点,一定符合条件 int maxX=p[p.size()-1].x; for(int i=p.size()-2;i>=0;i--){ //y从大到小,若i点x值大于所有比其y值大的点的x值,那么i点为“最大点”。 if(p[i].x>maxX){ res.push_back(p[i]); maxX=p[i].x; } } finish = clock(); cout<<"符合条件的点数量:"<<res.size()<<endl; for(int i=0;i<res.size();i++){ printf("%d %d\n", res[i].x, res[i].y); } totaltime=(double)(finish-start)/CLOCKS_PER_SEC; cout<<"\n此程序的运行时间为"<<totaltime<<"秒!"<<endl; return 0; }
输入点的个数和点:......输入总点数为:500000 ------------------过滤后再使用预排序:------------------------------ 过滤后点数量:648 符合条件的点数量:16 15480205 99999697 17427518 99999676 78059606 99999351 80881235 99998746 91608165 99997683 95825638 99996289 99690315 99993155 99874266 99991089 99884382 99978546 99908259 99961095 99942330 99858670 99963997 99157830 99975627 97385053 99996564 95654979 99998236 95378376 99999527 66461920 此程序的运行时间为0.013037秒! ------------------直接使用预排序:------------------------------ 符合条件的点数量:16 15480205 99999697 17427518 99999676 78059606 99999351 80881235 99998746 91608165 99997683 95825638 99996289 99690315 99993155 99874266 99991089 99884382 99978546 99908259 99961095 99942330 99858670 99963997 99157830 99975627 97385053 99996564 95654979 99998236 95378376 99999527 66461920 此程序的运行时间为0.288308秒!
下面的代码可以通过牛客网测试
#include<iostream> #include<algorithm> #include<vector> #include <cstdlib> using namespace std; struct point{ //定义结构体 int x,y; }; bool cmp(point a,point b){ //自定义排序方法 return a.y==b.y?a.x>b.x:a.y<b.y; //y升序,x降序 } point p[500001]; point filter[500001]; int main(){ int count; scanf("%d",&count); for(int i = 0; i < count; i++) { scanf("%d%d", &p[i].x, &p[i].y); } int curMaxRank = 0; int curMaxIndex = 0; for(int i=0;i<count;i++){ int temp =p[i].x+p[i].y-std::abs(p[i].x-p[i].y); if(temp > curMaxRank) { curMaxRank = temp; curMaxIndex = i; } } int fCount =0 ; for(int i=0;i<count;i++) { if(p[i].x >= p[curMaxIndex].x || p[i].y>= p[curMaxIndex].y) { filter[fCount++]=p[i]; } } sort(filter,filter+fCount,cmp); int maxx=-1; for(int i=fCount-1;i>=0;i--){ //y从大到小,若i点x值大于所有比其y值大的点的x值,那么i点为“最大点”。 if(filter[i].x>maxx){ printf("%d %d\n", filter[i].x, filter[i].y); maxx=filter[i].x; } } return 0; }
通过时间再200-300ms左右,和直接预排序的时间几乎相同,那么应该是牛客网的测试用例都比较特别,过滤起不到大的效果或者是输入输出占用了大部分时间,无论怎么优化算法都没办法减少打印时间。。。不过没关系,对于随机用例我们可以肯定该算法会更加优秀。
总结与展望
对于随机点进行大量测试,发现存在笔者给出的过滤方法,平均可以过滤99.9%的点。也就是说过滤后所剩点m的数量为原始点集n数量的千分之一。
使用过滤的额外好处是,我们只需要开辟千分之一的内存,然后就可以不改变原有点集的顺序,也就是说如果题目还有不改变原有点集的要求,依然可以满足 。
过滤付出的时间代价是线性的。那么算法的整体复杂度为O(n+ mlogm),而一般m值为n的千分之一。那么算法的平均复杂度为O(n),空间复杂度O(m)。通过上述代码实际对比,性能提高了大约20倍左右。使用O(m)空间,可以确保不改变原有点集的顺序。 可不可以继续优化,可以可以,优化永无止境,只要别轻易放弃思考。
本文更新了使用四叉树的数据结构来求解问题,对于随机测试点也有不错的性能。
如果对你有所帮助,点个赞呗~ 原创文章,请勿转载,谢谢


