基于可见性图的最短路径规划

 

实现效果；

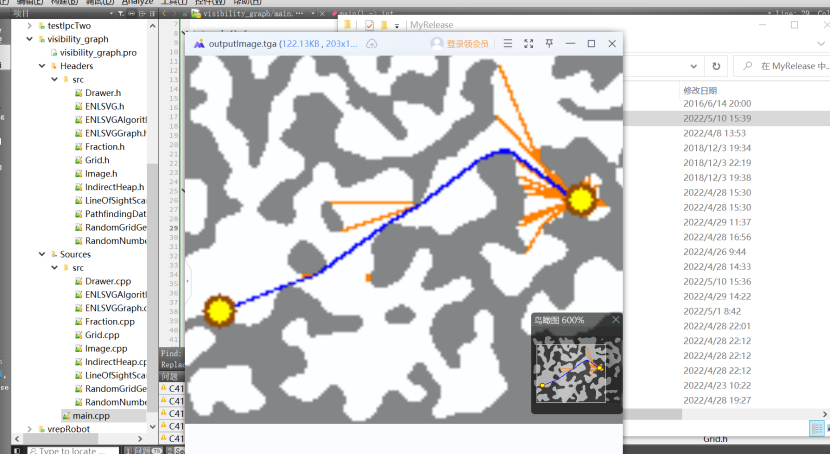
建立地图相关数据结构很耗时，适合离线路径规划

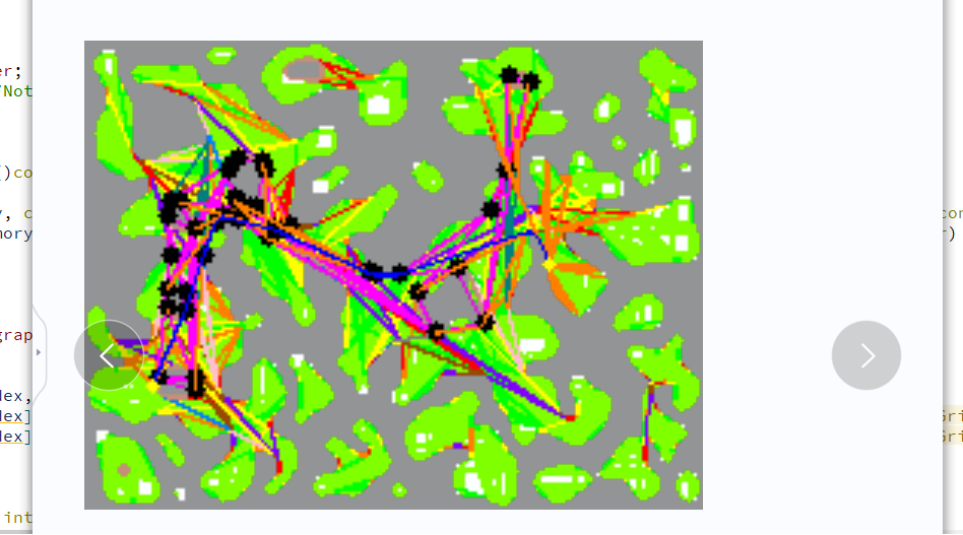
 可见性图的建立会比较复杂，障碍物都会转换为多边形，convex或者concave;

地图转换为多边形考虑使用approxypoly轮廓多边形拟合或者使用ros中的costmap_convertor;

 

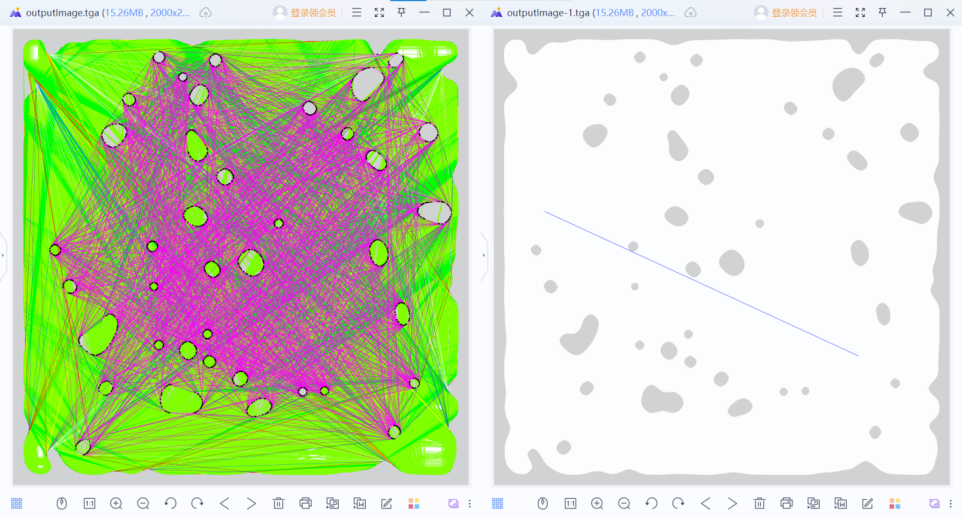
visibility graph原理 

 

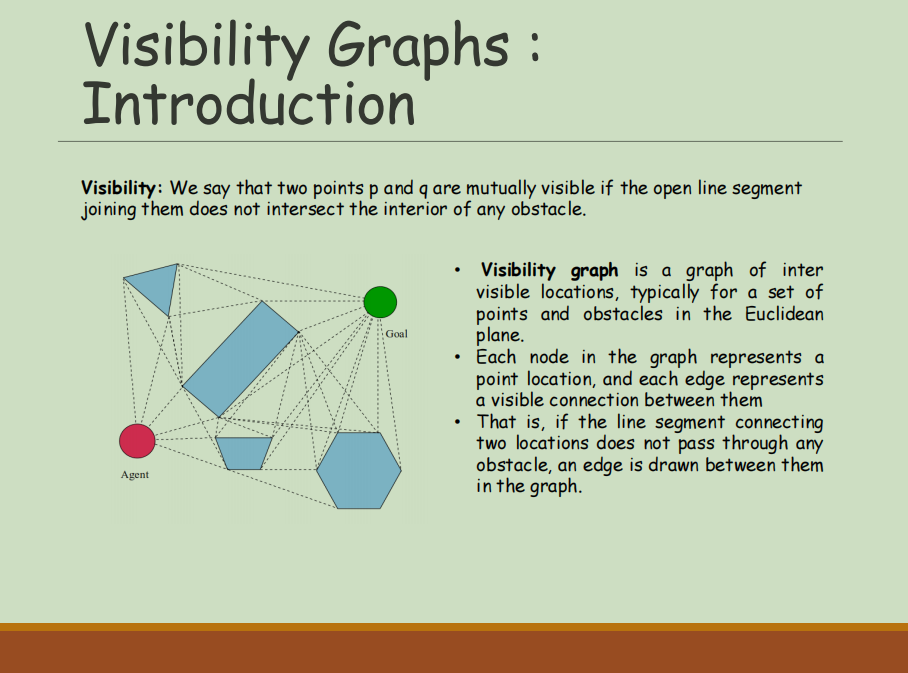
why use visibilty graph?

给定平面上一些多边形障碍物和两个障碍物之外的点，可以据此找到不穿过障碍物的最短路径；

优化处理

 

 

 如上图中，指向凸多边形内部的edge可以直接去掉；因为两边之和大于第三边；这样做可以减少搜索时间；

处理之后称之为reduced visibility graph;

可见性图的应用

最短路径搜索；（把起点和终点和多边形顶点一起建立 visibility graph，然后使用图论最短路径搜索,使用dijkstra）

艺术画廊问题；

 

参考文献

1. https://en.wikipedia.org/wiki/Visibility_graph 

2. http://cs.smith.edu/~streinu/Teaching/Courses/274/Spring98/Proje

cts/Philip/fp/visibility.htm

3. http://www.cs.wustl.edu/~pless/546/lectures/l22.html 

4. Choset, Howie M. Principles of robot motion: theory, algorithms, and

implementation. MIT press, 2005.