线性代数及其应用（最小二乘、PCA、SVD）
第六章 正交性与最小二乘
正交投影（可以用于正交化、解释最小二乘，QR分解用于最小二乘）
最小二乘也是唯一的
正交化方法
使用正交基计算投影（用于最小二乘）
QR分解（使用正交化方法）
最小二乘问题的几何描述（寻找距离最近的投影）
有唯一解的条件
另一种解法
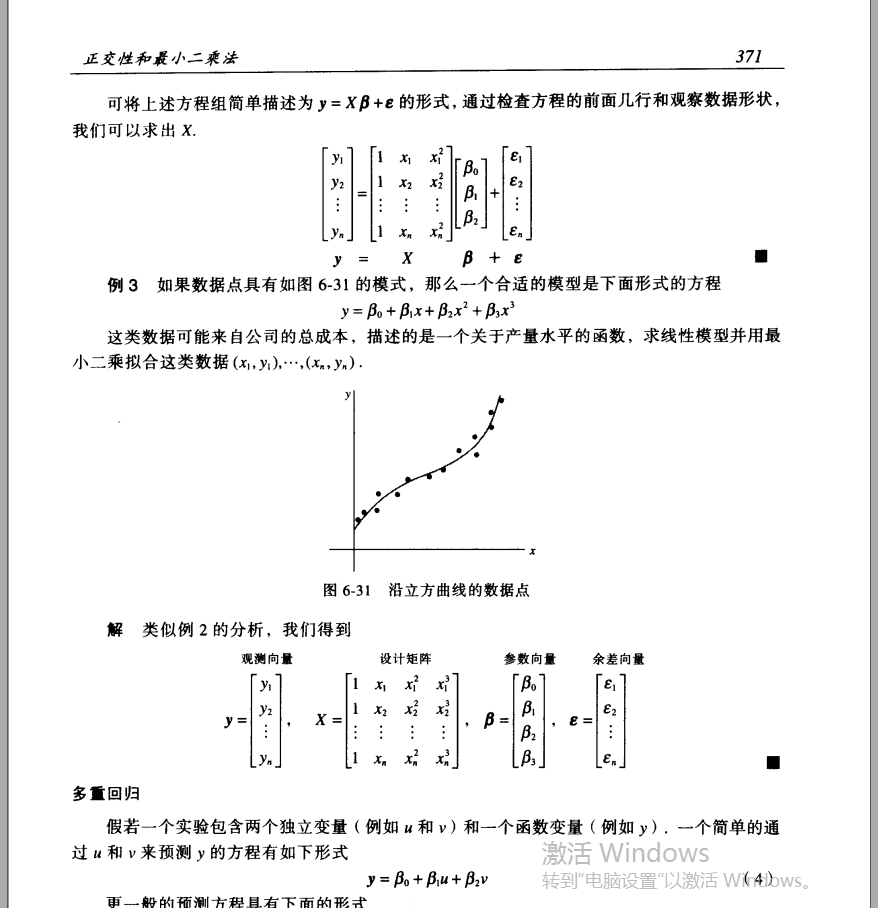
其他曲线的最小二乘拟合
对称矩阵和二次型
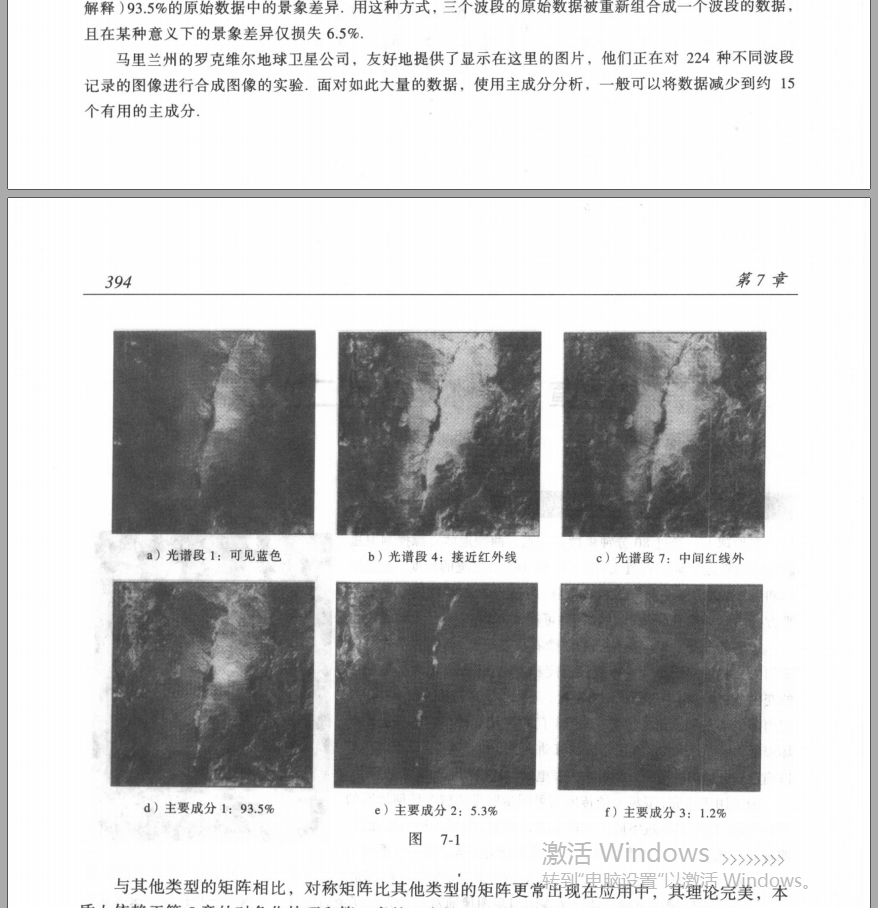
将多种像素重新线性组合，使得合成的图像景象差异更加明显。
对称矩阵的对角化
谱分解(特征值反映了在对应的特征向量的子空间投影的权重，例如A表示将圆映射为椭圆的矩阵，则其特征值反映了长轴和短轴)
特征值分解可以用于数据压缩（只需要大的特征值和对应的特征向量就可以近似原来的矩阵）
主轴定理（去掉二次型的交叉项）
通过特征值求解二次型最大值
有条件限制时求解最大值（单位球上的向量，在第二大特征值特征向量方向取得）
奇异值分解
使用二次型求解最大拉伸方向
注意Av是A的列空间的正交基
注意Av是A的列空间的正交基
奇异值分解的步骤
莫尔逆矩阵：直接得到b在A的列空间的正交投影，直接求解最小二乘x
主成分分析（正交回归）：可以使得不同维度分量组合后的方差最大，或者是得到使得投影后方差最大的方向。计算协方差矩阵的特征值，用对应的特征向量作为权值将原变量线性组合，使得组合后的变量方差最大。
PCA把原先的n个特征用数目更少的m个特征取代，新特征是旧特征的线性组合，这些线性组合最大化样本方差，尽量使新的m个特征互不相关。
计算方法：
1.有m个d-维数据，每个d维数据表示为列向量，将列向量拼成m列。得到d行m列的矩阵。
2.计算协方差矩阵。
3.计算S的特征值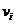
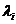
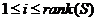
4.选取前k个最大特征根对应的特征向量，得到矩阵
5.AX相乘得到投影矩阵。
PCA把原先的n个特征用数目更少的m个特征取代，新特征是旧特征的线性组合，这些线性组合最大化样本方差，尽量使新的m个特征互不相关。
