求平面散点集的凸包
本文参考自<<算法导论>>章节33.3 寻找凸包
Graham算法主要利用向量的叉积判断点和线段的位置关系,详见 向量叉积,然后从左下角点按逆时针方向寻找最边缘的线段,利用的原理就是从凸包上任意一点逆时针出发,每到一个节点,一定会向左拐.算法复杂度为O(nlg(n))
算法主要实现如下:
1 // 输入:点数组arrInPt,个数nInPtCount,包含所有点 2 // 输出:点数组arrOutPt,个数nOutPtCount,逆时针顺序依次存放凸包上的点 3 static void Graham(Point arrInPt[],const int nInPtCount,Point arrOutPt[],int & nOutPtCount) 4 { 5 // step 1:找到最靠近坐下角的点,放到p[0]位置 6 // 保证p[0]的y值最小,若两点y值相同,取x值较小者 7 int nIndex = 0; 8 for(int i = 1;i < nInPtCount;++i) 9 { 10 if(arrInPt[i].y < arrInPt[nIndex].y || 11 (arrInPt[i].y == arrInPt[nIndex].y && arrInPt[i].x < arrInPt[nIndex].x)) 12 { 13 nIndex = i; 14 } 15 } 16 Point tmp = arrInPt[0]; 17 arrInPt[0] = arrInPt[nIndex]; 18 arrInPt[nIndex] = tmp; 19 20 // step 2:剩下的点p[1]--p[nInPtCount-1],按照与p[0]极角升序排序 21 SortByPolarAngle(arrInPt,nInPtCount); 22 23 // step 3:栈操作 24 nOutPtCount = 0; 25 // 前三个点入栈 26 arrOutPt[nOutPtCount++] = arrInPt[0]; 27 arrOutPt[nOutPtCount++] = arrInPt[1]; 28 arrOutPt[nOutPtCount++] = arrInPt[2]; 29 for(int i = 3;i < nInPtCount;i++) 30 { 31 // 栈中最上面两个点如果不与arrInPt[i]形成左转,就进行出栈操作 32 while(nOutPtCount > 1 && IfTurnLeft(arrOutPt[nOutPtCount-2],arrOutPt[nOutPtCount-1],arrInPt[i]) == false ) 33 { 34 nOutPtCount--; 35 } 36 // arrInPt[i]入栈 37 arrOutPt[nOutPtCount++] = arrInPt[i]; 38 } 39 }
Jarvis算法与Graham算法类似也是从左下角的点开始,依次搜寻与边界点极角最小的点.算法复杂度为O(hn),h为边界点的个数
1 // 输入:点数组arrInPt,个数nInPtCount,包含所有点 2 // 输出:点数组arrOutPt,个数nOutPtCount,逆时针顺序依次存放凸包上的点 3 static void Jarvis(Point arrInPt[],const int nInPtCount,Point arrOutPt[],int & nOutPtCount) 4 { 5 // step 1:找到最靠近坐下角的点,放到p[0]位置 6 // 保证p[0]的y值最小,若两点y值相同,取x值较小者 7 nOutPtCount = 0; 8 int nIndex = 0; 9 for(int i = 1;i < nInPtCount;++i) 10 { 11 if(arrInPt[i].y < arrInPt[nIndex].y || 12 (arrInPt[i].y == arrInPt[nIndex].y && arrInPt[i].x < arrInPt[nIndex].x)) 13 { 14 nIndex = i; 15 } 16 } 17 Point tmp = arrInPt[0]; 18 arrInPt[0] = arrInPt[nIndex]; 19 arrInPt[nIndex] = tmp; 20 // step : 寻找与p[nIndex]极角最小的那个点 21 nIndex = 0; 22 do 23 { 24 arrOutPt[nOutPtCount++] = arrInPt[nIndex]; 25 nIndex = FindMinPolarAngle(arrInPt,nInPtCount,nIndex); 26 } while (arrInPt[0] != arrInPt[nIndex]); 27 }
经测试,两种算法的效率差不多,10W个点以内,1s之内可以搞定,100w个点,Jarvis大约需要5秒多,Graham大约需要6s多,也就是h < log(n)时,Jarvis效率略优.测试机器为i5 3.10GHz
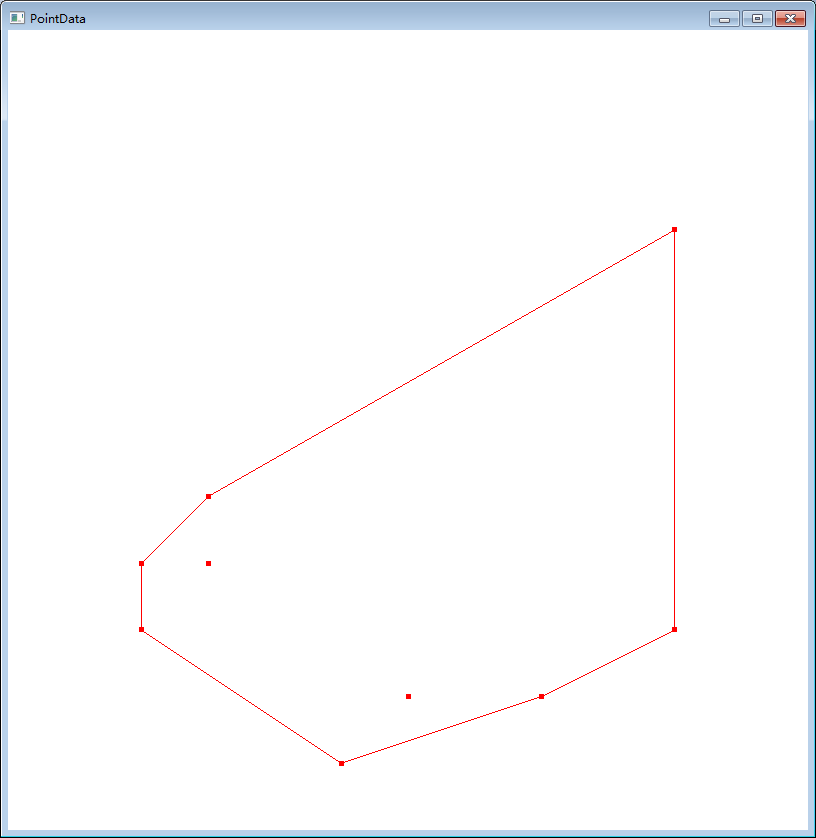
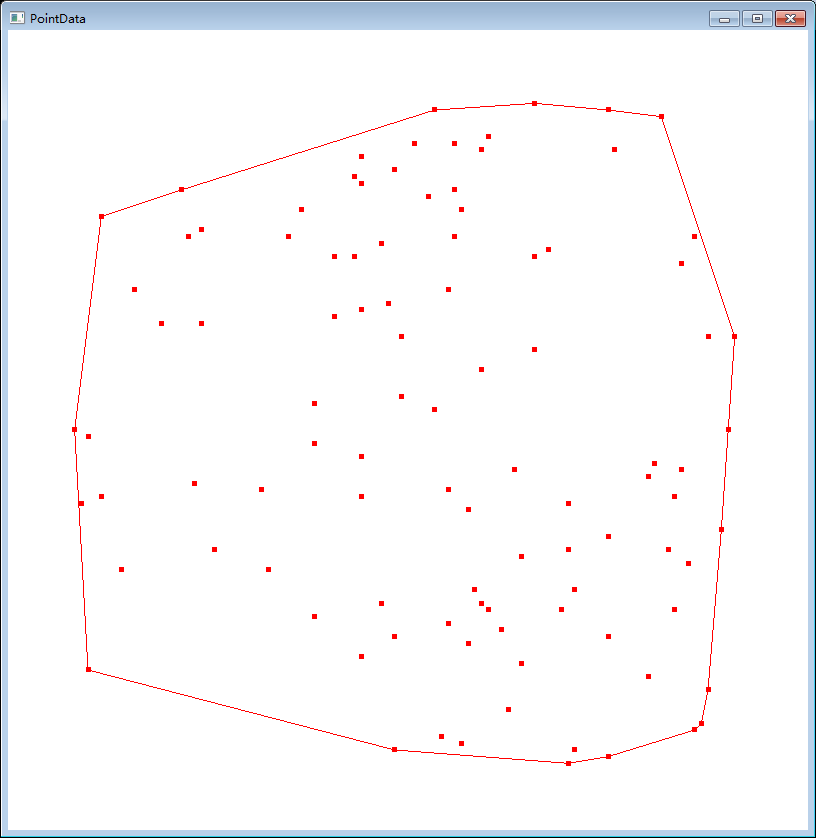

Graham效率:

Jarvis效率: