转:用三段 140 字符以内的代码生成一张 1024×1024 的图片
原文转自 :http://blogread.cn/it/article/6899?f=wb&from=timeline&isappinstalled=1
Kyle McCormick 在 StackExchange 上发起了一个叫做 Tweetable Mathematical Art 的比赛,参赛者需要用三条推这么长的代码来生成一张图片。具体地说,参赛者需要用 C++ 语言编写 RD 、 GR 、 BL 三个函数,每个函数都不能超过 140 个字符。每个函数都会接到 i 和 j 两个整型参数(0 ≤ i, j ≤ 1023),然后需要返回一个 0 到 255 之间的整数,表示位于 (i, j) 的像素点的颜色值。举个例子,如果 RD(0, 0) 和 GR(0, 0) 返回的都是 0 ,但 BL(0, 0) 返回的是 255 ,那么图像的最左上角那个像素就是蓝色。参赛者编写的代码会被插进下面这段程序当中(我做了一些细微的改动),最终会生成一个大小为 1024×1024 的图片。
很多牛人贡献出了自己写的代码,生成了精美的图片,我觉得很有意思,自己试验了下他们的代码,摘录几段如下:

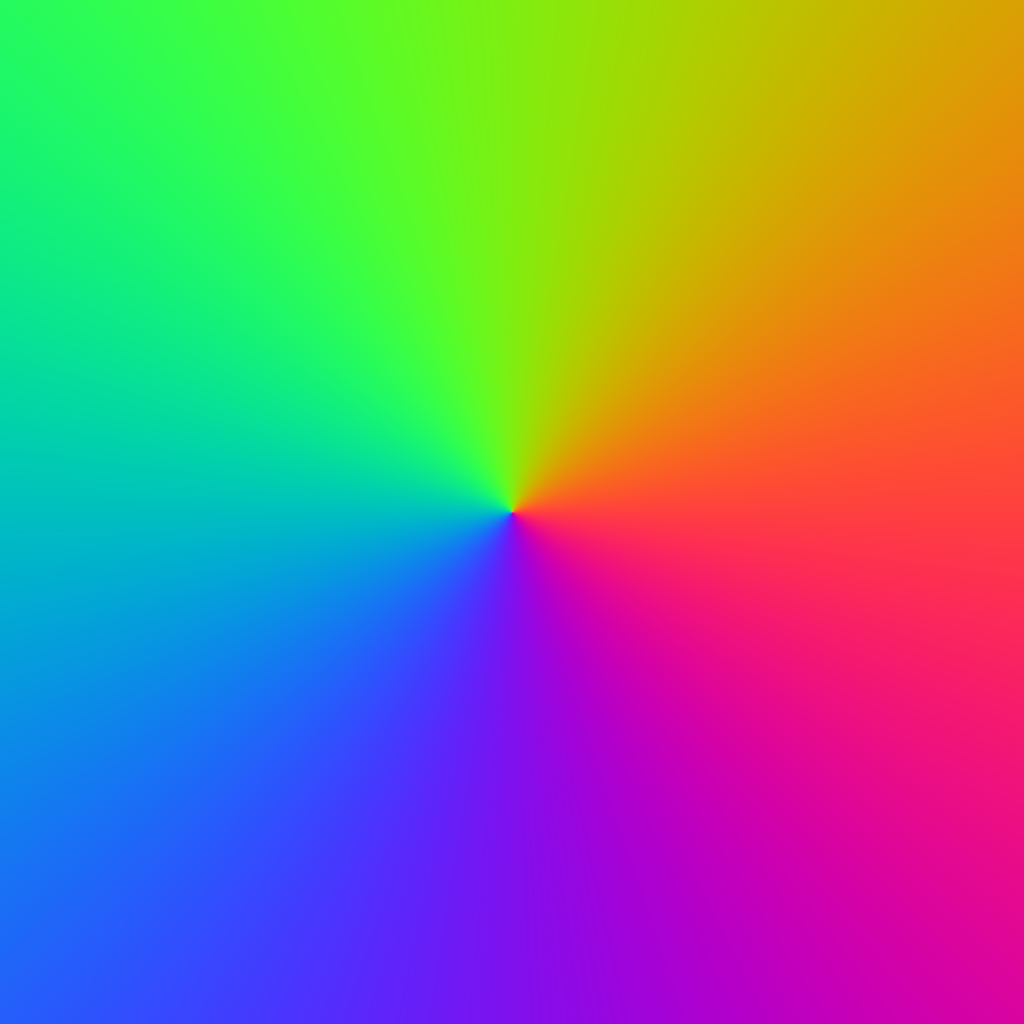
1 #include <iostream> 2 #include <cmath> 3 #include <cstdlib> 4 #include <time.h> 5 using namespace std; 6 7 #define DIM 1024 8 #define NAME_LEN 256 9 #define DM1 (DIM-1) 10 #define _sq(x) ((x)*(x)) // square 11 #define _cb(x) abs((x)*(x)*(x)) // absolute value of cube 12 #define _cr(x) (unsigned char)(pow((x),1.0/3.0)) // cube root 13 14 unsigned char RD(int,int,int); 15 unsigned char GR(int,int,int); 16 unsigned char BL(int,int,int); 17 18 unsigned char RD(int t,int i,int j){ 19 switch(t) 20 { 21 case 0: 22 { 23 return (char)(_sq(cos(atan2(j-512,i-512)/2))*255); 24 } 25 case 1: 26 { 27 #define r(n)(rand()%n) 28 static char c[1024][1024]; 29 return !c[i][j]?c[i][j]=!r(999)?r(256):RD(t,(i+r(2))%1024,(j+r(2))%1024):c[i][j]; 30 } 31 case 2: 32 { 33 float x=0,y=0; 34 int k; 35 for(k=0;k++<256;) 36 { 37 float a=x*x-y*y+(i-768.0)/512;y=2*x*y+(j-512.0)/512; 38 x=a;if(x*x+y*y>4) 39 break; 40 } 41 return log(k)*47; 42 } 43 case 3: 44 { 45 double a=0,b=0,c,d,n=0; 46 while((c=a*a)+(d=b*b)<4&&n++<880) 47 { 48 b=2*a*b+j*8e-9-.645411;a=c-d+i*8e-9+.356888; 49 } 50 return 255*pow((n-80)/800,3.); 51 } 52 case 4: 53 { 54 static double k; 55 k+=rand()/1./RAND_MAX; 56 int l=k; 57 l%=512; 58 return l>255?511-l:l; 59 } 60 case 5: 61 { 62 float s=3./(j+99); 63 float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM)*35)*s; 64 return (int((i+DIM)*s+y)%2+int((DIM*2-i)*s+y)%2)*127; 65 } 66 case 6: 67 { 68 #define D DIM 69 #define M m[(x+D+(d==0)-(d==2))%D][(y+D+(d==1)-(d==3))%D] 70 #define R rand()%D 71 #define B m[x][y] 72 return(i+j)?256-(BL(t,i,j))/2:0; 73 } 74 default: 75 { 76 return 0; 77 } 78 } 79 } 80 unsigned char GR(int t,int i,int j){ 81 switch(t) 82 { 83 case 0: 84 { 85 return (char)(_sq(cos(atan2(j-512,i-512)/2-2*acos(-1)/3))*255); 86 } 87 case 1: 88 { 89 static char c[1024][1024]; 90 return !c[i][j]?c[i][j]=!r(999)?r(256):GR(t,(i+r(2))%1024,(j+r(2))%1024):c[i][j]; 91 } 92 case 2: 93 { 94 float x=0,y=0; 95 int k; 96 for(k=0;k++<256;) 97 { 98 float a=x*x-y*y+(i-768.0)/512; 99 y=2*x*y+(j-512.0)/512; 100 x=a; 101 if(x*x+y*y>4) 102 break; 103 } 104 return log(k)*47; 105 } 106 case 3: 107 { 108 double a=0,b=0,c,d,n=0; 109 while((c=a*a)+(d=b*b)<4&&n++<880) 110 { 111 b=2*a*b+j*8e-9-.645411;a=c-d+i*8e-9+.356888; 112 } 113 return 255*pow((n-80)/800,.7); 114 } 115 case 4: 116 { 117 static double k; 118 k+=rand()/1./RAND_MAX; 119 int l=k; 120 l%=512; 121 return l>255?511-l:l; 122 } 123 case 5: 124 { 125 float s=3./(j+99); 126 float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM)*35)*s; 127 return (int(5*((i+DIM)*s+y))%2+int(5*((DIM*2-i)*s+y))%2)*127; 128 } 129 case 6: 130 { 131 #define A static int m[D][D],e,x,y,d,c[4],f,n;if(i+j<1){for(d=D*D;d;d--){m[d%D][d/D]=d%6?0:rand()%2000?1:255;}for(n=1 132 return RD(t,i,j); 133 } 134 default: 135 { 136 return 0; 137 } 138 } 139 } 140 unsigned char BL(int t,int i,int j){ 141 switch(t) 142 { 143 case 0: 144 { 145 return (char)(_sq(cos(atan2(j-512,i-512)/2+2*acos(-1)/3))*255); 146 } 147 case 1: 148 { 149 static char c[1024][1024]; 150 return !c[i][j]?c[i][j]=!r(999)?r(256):BL(t,(i+r(2))%1024,(j+r(2))%1024):c[i][j]; 151 } 152 case 2: 153 { 154 float x=0,y=0; 155 int k; 156 for(k=0;k++<256;) 157 { 158 float a=x*x-y*y+(i-768.0)/512; 159 y=2*x*y+(j-512.0)/512; 160 x=a; 161 if(x*x+y*y>4) 162 break; 163 } 164 return 128-log(k)*23; 165 } 166 case 3: 167 { 168 double a=0,b=0,c,d,n=0; 169 while((c=a*a)+(d=b*b)<4&&n++<880) 170 { 171 b=2*a*b+j*8e-9-.645411;a=c-d+i*8e-9+.356888; 172 } 173 return 255*pow((n-80)/800,.5); 174 } 175 case 4: 176 { 177 static double k; 178 k+=rand()/1./RAND_MAX; 179 int l=k; 180 l%=512; 181 return l>255?511-l:l; 182 } 183 case 5: 184 { 185 float s=3./(j+99); 186 float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM)*35)*s; 187 return (int(29*((i+DIM)*s+y))%2+int(29*((DIM*2-i)*s+y))%2)*127; 188 } 189 case 6: 190 { 191 A;n;n++){x=R;y=R;if(B==1){f=1;for(d=0;d<4;d++){c[d]=M;f=f<c[d]?c[d]:f;}if(f>2){B=f-1;}else{++e%=4;d=e;if(!c[e]){B=0;M=1;}}}}} 192 return m[i][j]; 193 } 194 default: 195 { 196 return 0; 197 } 198 } 199 } 200 void draw_pic(int); 201 void pixel_write(int,int,int,FILE*); 202 203 int main(){ 204 time_t t1,t2; 205 for(int i = 0;i < 7;i++) 206 { 207 t1 = clock(); 208 draw_pic(i); 209 t2 = clock(); 210 cout<<"use time:"<<t2 - t1<<"(ms)"<<endl; 211 } 212 return 0; 213 } 214 215 void draw_pic(int t) 216 { 217 FILE *fp = NULL; 218 char name[NAME_LEN] = {0}; 219 sprintf(name,"MathPic_%d.ppm",t); 220 cout<<"rendering "<<name<<"..."<<endl; 221 fp = fopen(name,"wb"); 222 if(fp == NULL){ 223 return; 224 } 225 fprintf(fp, "P6\n%d %d\n255\n", DIM, DIM); 226 for(int j=0;j<DIM;j++){ 227 for(int i=0;i<DIM;i++){ 228 pixel_write(t,i,j,fp); 229 } 230 } 231 fclose(fp); 232 cout<<"render "<<name<<" finished"<<endl; 233 } 234 void pixel_write(int t,int i, int j,FILE* fp){ 235 static unsigned char color[3]; 236 color[0] = RD(t,i,j)&255; 237 color[1] = GR(t,i,j)&255; 238 color[2] = BL(t,i,j)&255; 239 fwrite(color, 1, 3, fp); 240 }
图片效果如下