1-数据结构
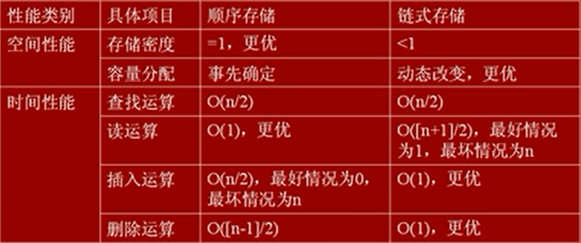

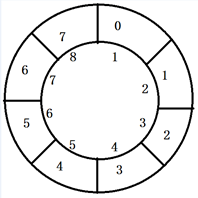
此类题目最好的解决方法就是使用例子
- 首先由题目知道,这是一个循环队列,循环队列中只有mod才能进行有效的数据存储,所以A D被排除
- 由左图知道m是最后一个元素 所以 m = 8
- rear表示队尾的实际位置,7的实际位置时8,因为7是队列的第八个数据,则得出rear = 8
- length = 8
- C B 公式可得 C = 1 B = 0
- 此题目问的是队首元素的实际位置,我们这个队列队首是0,她的实际位置时
- 所以此题选择C
树
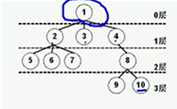
节点的度:就是一个节点下分的子节点的个数
1号节点的度为3
8号节点的度为2
树的度:就是该树中最大的节点度
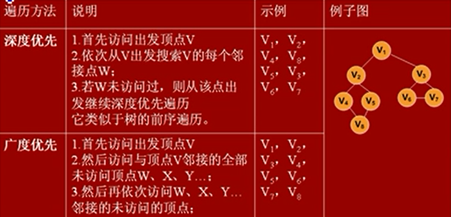
树的遍历(这个我明白)
1. 前序遍历
2. 中序遍历
3. 后序遍历
4. 层次遍历
题目:

关于二叉树的常用公式
n 0= n2+1
也就是说,叶子节点数总是比度为2的节点多一个
解题思路:
n (全部节点个数)= n2+n1+n0
767=n2+n1+n0; 带入上边的公式
(768-n1)/2=n0
我们由完全二叉树知道,其实,完全二叉树中度为1的节点,只要两种可能 0个或1个
当n1=1时,n0为小数,不科学,所以n1=0 n0 = 384
树及其二叉树
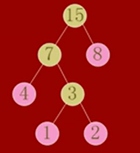
概念:
树的路径长度:将树中所有的路径相加
例:上图中树的路径长度为6
权:就是给一个节点的特殊概念,就是计算机在这个程序中需要访问的次数
例:上图中编号为2的节点,权就是2 也就是计算机在这个程序中访问他两次
带权路径长度:就是到达这个节点的路径*权值
例:上图中编号为2 的节点,带权路径长度为3*2 = 6,
树 的带权路径长度:把所有的节点的带权路径长度相加
最优二叉树(哈夫曼树)
就是树的带权路径长度最小的树



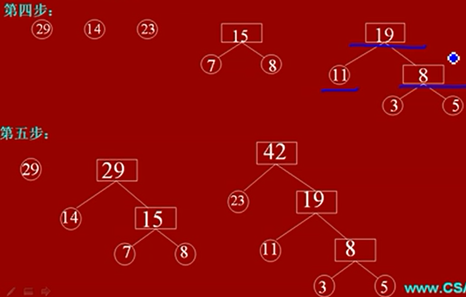
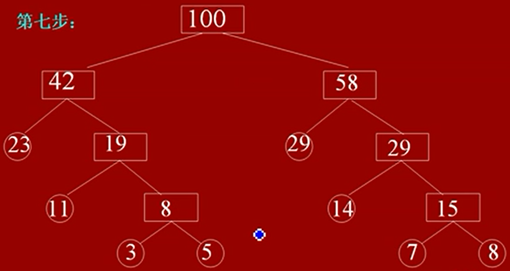
注意:在此树中,树的带权路径是由所有圆圈节点的带权路径相加的,并不包括方框的节点
那是因为,圆圈才是我们的数据,而方框只是用来进行构建树而出现的,
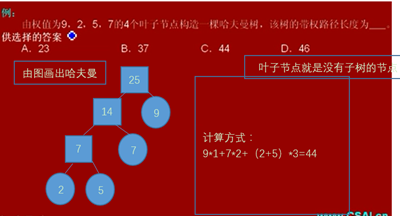

叶子节点就是没有子树的节点,由下图可以得出,为5

查找二叉树,二叉排序树
通俗来讲:就是所有节点由左向右依次权值增加
定义:左树为非空时,左树一定比根节点小
右树为非空时,右树一定比根节点大
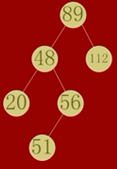
图
图的构成:
G=(V,E)
V:是有限的非空定点集合
E:是边与边之间的集合
图分为有向图和无向图
表示方式:
有向图:<A,B>
无向图:(A,B)
顶点的度:无向图:与顶点与之关联的边
有向图:入度和出度
子图:边和节点都在另一个图中存在。
完全图:在无向图中,若每对顶点之间都有一条边相连成为完全图
有向图:每对顶点之间都有两条有向边相连
路径和回路:
路径:从一个节点到另一个节点所走的边的个数
回路:从一个节点出发,最终回到这个节点
简单回路:除了开始节点和结束节点是相同 的,中间没有相同的节点
连通图和连通分量:
连通图:图中任意两个节点都可以到达,就是连通图
连通分量:就是一个总图中,有一小部分是连通的,则他就是总图的连通分量
网络:
每一个图的节点都有一个权值
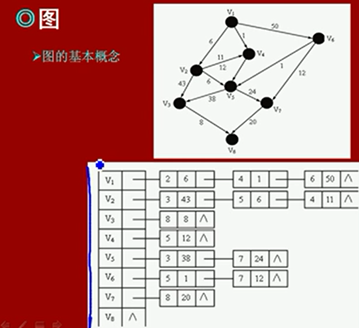
图的遍历
图的最小生成树
普利姆算法:从点着手
克鲁斯卡尔:从边着手
AOV网络:
用有向边表示活动之间开始的先后关系
这种有向图称为AOV网络
拓朴排序:
- 找入度为0的节点
- 将零的出度全部删去
- 再持续以上两步,知道该图全部完成
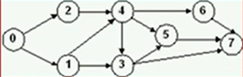
上图的拓扑排序有

关键路径(重点难点)
注意:其实就是最长路径
AOE网络
把AOV网上,每一个边,加上一个权值就成为了AOE
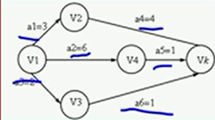
关键路径的几个重要概念:
顶点n的最早发生时间:就是从原点到顶点的最长路径长度,记做Ve(n)
例如:Vk的最早发生时间是7
原因是,Vk若想启动,需要a4,a5,a6,全部完成,虽然a6+a3=3哥个时间
但是,如果a5,和a4没有完成,则Vk也是没法启动的
活动a的最早开始时间:活动a就是边,是从起点到他上一个顶点的完成时间 记做:e(a)
例如:a5的最早开始时间是第六时刻,a6的最早开始时间是2
顶点n的最迟发生时间:在不影响工程的情况下Vk 记做:VI(n)
例如:V3的最迟发生时间是第六时间,因为a6只有1个时间,而且全部工程的最早完成时间是7
即便v3在第六时间完成,他也是可以在vk的最早发生时间完成
活动a的最迟开始时间:记做I(n)
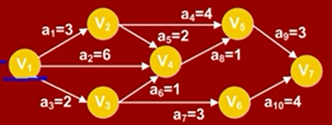
上图中:Ve(7)=10;



