数组中的逆序对
#Problem Description:
#在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。
#输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。
#即输出P%1000000007
看到这题马上就想到用从前往后依次扫描数组,固定第一位,遍历时每遇到小于本身时加一,但是这样的时间复杂度为O(n²),不太可取,讨论组建议采用归并排序,归并排序在最好情况时间复杂度为O(n),最坏时也才O(nlogn)。
stepA 归并排序算法实现
归并排序是经典排序算法之一,其核心是将待排数组不断细分,然后排序最后再合并,这是经典的分治策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之),借用大佬一张图来说明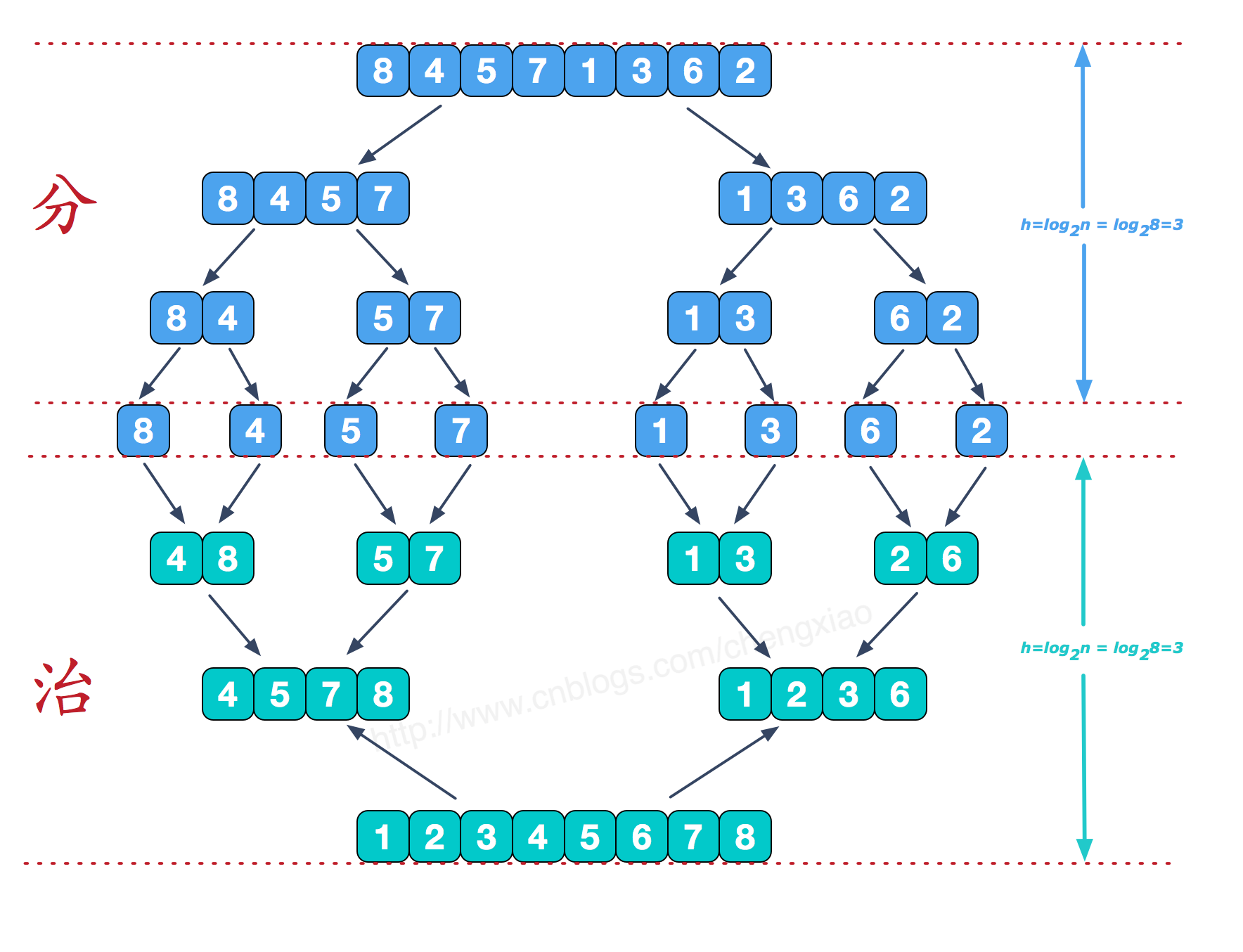
看看分治的代码:
class Solution: tempList = [] def InversePairs(self,data): r = len(data)-1 self.tempList = ['*']*len(data) self.divide(data,0,r) return self.count
#递归从中间位划分为左右两块,当划分为1时进行合并 def divide(self,data,l,r): if l<r: center = (l+r)/2 self.divide(data,l,center) self.divide(data,center+1,r) self.merge(data,l,center,r) def merge(self,data,l,center,r): i = l; j = center+1; t = 0 while i<=center and j<=r:
#左边大于了右边,将右边放入临时数组,右边和临时数组下标都+1 if data[i]>data[j]: self.tempList[t] = data[j] j += 1 t += 1
#反之,则将左边放入临时数组,左边和临时数组下标都+1 else: self.tempList[t] = data[i] i += 1 t += 1
#上述过程完成后,左边仍然小于中间位,证明左边较大,则遍历依次放入临时数组 while i<=center: self.tempList[t] = data[i] t += 1 i += 1
#反之,将右边放入临时数组 while j<=r: self.tempList[t] = data[j] t += 1 j += 1 t=0
#最终,将临时数组拷贝到原数组 while l<=r: data[l] = self.tempList[t] l += 1 t += 1 data = data = [1,2,3,4,5,6,7,0] s = Solution() print(s.InversePair(data))
StepB 逆序对的统计
python定义两个函数,divide()主要实现对数组的二分,采用递归方法,先左再右,merge()函数主要实现对数组的排序,设计两个指针分别指向两个数组第一个位置,比较其大小,将小的放入临时数组中然后指针往后移动一位,最后如果某一个数组位置已经到最大,则将另一个数组的剩余数字依次放入临时数组中,最后再把临时数值拷贝到原数组中,至此,此趟排序完成。
那要统计逆序对要怎么修改呢,一开始的思路是,在i<j &&data[i]>data[j] 的情况下,用center-i+1统计,因为两个数组已经排好序,如果第一个数组中前一个位已经大于后一个数组指针对应的位置,那么第一个数组剩下的位数都将大于后一个数组,然后循环累加的方法,自己做了一些小的数据集测试没有出现问题,但是牛客却通不过验证,所以选择<<剑指offer>>上的将两个指针放在两个数组从后往前扫描,只要前一个数组最后一位比后一个数组最后一位都大,那前一个数组比后一个数组剩余的所有的位都大,j-center 最后做统计输出。完整代码如下:
class Solution2: count = 0 def InversePairs(self,data): r = len(data)-1 tempList = ['*']*len(data) self.divide(data,0,r,tempList) return self.count%1000000007 def divide(self,data,l,r,tempList): if l<r: center = (l+r)/2 self.divide(data,l,center,tempList) self.divide(data,center+1,r,tempList) self.merge(data,l,center,r,tempList) def merge(self,data,l,center,r,tempList): i = center j = r t = r while i>=l and j>center: if data[i]>data[j]: tempList[t] = data[i] i -= 1 t -= 1 #逆序对核心代码 self.count += j-center else: tempList[t] = data[j] j -= 1 t -= 1 while i>=l and t>=0: tempList[t] = data[i] t -= 1 i -= 1 while j>center and t>=0: tempList[t] = data[j] t -= 1 j -= 1 while r>=l: data[r] = tempList[r] r -= 1 data = [1,2,3,4,5,6,7,0] s = Solution2() print(s.InversePair(data))
提交之后发现还是出问题了:

case通过率75%,看它的测试集数量才知道有2*10^5那么多,估计运行时间太长了,时间复杂度还是太高。

看到讨论组又有人提出了另外一种思路叫做树状数组,赶紧研究去。
StepC 树状数组的实现
先看下树状数组的逻辑结构图,A是我们的普通数组,C就是树状数组了,可以看出,树状数组下标为奇数的节点的值就等于原数组下标对应的值,但偶数时就出现变化了,这种变化就是树状数组的特性,区间的和存储在偶数位上,而我们要求区间的和不用遍历整个数组,而是通过定义一个lowbit()函数就能知道该偶数位的和通过哪几个数就能计算出来。
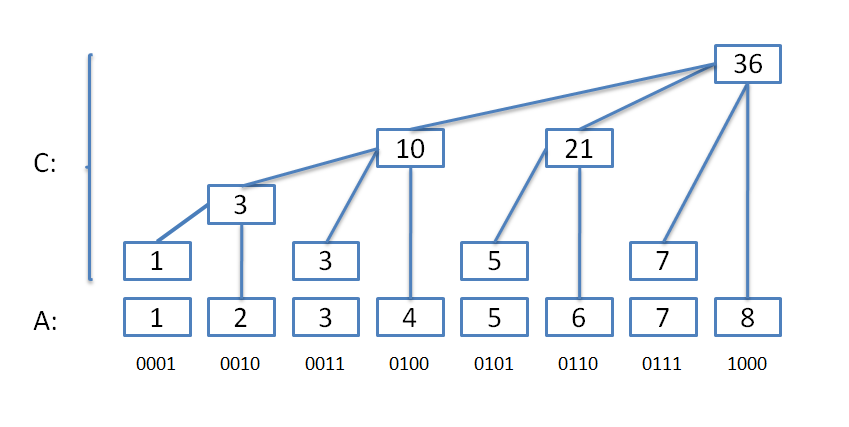
lowbit()函数就是求二进制中最低一位1,比如 5转换为二进制位0101,最低位1为0001,所以lowbit(5)=1,lowbit(7)=1。求lowbit的两种方法:
#从右向左找到第一个1(这个1就是我们要求的结果,但是现在表示不出来,后来的操作就是让这个1能表示出来),
#这个1不要动和这个1右边的二进制不变,左边的二进制依次取反,这样就求出的一个数的补码
def lowbit(self,x): return x&-x
#先消掉最后一位1,然后再用原数减去消掉最后一位1后的数
def lowbit(self,x):
return x - (x & (x - 1))
求出lowbit()之后,当前位的和就等于从当前位开始向左求lowbit()个数的和,比如:
C1 = A1
C2 = A2+C1
C3 = A3
C4 = A4+C3+C2
C5 = A5
C6 = A6+C5
C7 = A7
C8 = A8+C7+C6+C4
运用上面的思路,写出树状数组区间求和函数:
def getSum(self,n): cSum = 0 while n>0: cSum += self.c[n] n -= self.lowbit(n) return cSum
同时树状数组插入新的数时,则是将上述函数逆过程:
def update(self,i,n): while i<n: self.c[i] += 1 i += self.lowbit(i)
现在函数都定义好了,怎么用树状数组求逆序数呢?
StepD 树状数组求逆序对
定义一个数组数组c[],先将c中数值全部设为0,原始数据为data[], i 为遍历data的变量值,每当从data中取出值放入c中,先更新c中下标为data[i]的数值为1,即 c[ data[i] ]=1, 然后调用getsum()函数计算c中比data[i]小的值的个数,最后用 i-getsum(data[i])+1求出该数的逆序数。最后将所有数都插入c后统计逆序数总数。
举个例子:
data = [5,2,1,4,3]
c = [0,0,0,0,0]
1,输入5,调用update(5, 1),把第5位设置为1
1 2 3 4 5 0 0 0 0 1 计算1-5上比5小的数字存在么? 这里用到了树状数组的getSum(5) = 1操作,现在用输入的下标1 - getSum(5) = 0 就可以得到对于5的逆序数为0。 2. 输入2,调用update(2, 1),把第2位设置为1 1 2 3 4 5 0 1 0 0 1 计算1-2上比2小的数字存在么? 这里用到了树状数组的getSum(2) = 1操作,现在用输入的下标2 - getSum(2) = 1 就可以得到对于2的逆序数为1。 3. 输入1,调用update(1, 1),把第1位设置为1 1 2 3 4 5 1 1 0 0 1 计算1-1上比1小的数字存在么? 这里用到了树状数组的getSum(1) = 1操作,现在用输入的下标 3 - getSum(1) = 2 就可以得到对于1的逆序数为2。 4. 输入4,调用update(4, 1),把第5位设置为1 1 2 3 4 5 1 1 0 1 1 计算1-4上比4小的数字存在么? 这里用到了树状数组的getSum(4) = 3操作,现在用输入的下标4 - getSum(4) = 1 就可以得到对于4的逆序数为1。 5. 输入3,调用update(3, 1),把第3位设置为1 1 2 3 4 5 1 1 1 1 1 计算1-3上比3小的数字存在么? 这里用到了树状数组的getSum(3) = 3操作,现在用输入的下标5 - getSum(3) = 2 就可以得到对于3的逆序数为2。
6. 0+1+2+1+2 = 6 这就是最后的逆序数
最后给出完整python解决方法:
class Solution3: aa = [] c = [] count = 0 nMax = 0 n = 0 def lowbit(self,x): return x&-x def getSum(self,n): cSum = 0 while n>0: cSum += self.c[n] n -= self.lowbit(n)
#加入0位判断 if self.c[0]==1: cSum += 1 return cSum def update(self,i,n):
#加入0位判断
if i==0: self.c[i] = 1 return while i<n: self.c[i] += 1 i += self.lowbit(i)def findMaxNumber(self,data): maxNumber = data[0] for i in range(1,len(data)): if maxNumber<data[i]: maxNumber = data[i] return maxNumber def InversePairs(self,data): dataLen = len(data) self.nMax = self.findMaxNumber(data) n = self.nMax+1 self.aa = data self.c = [0]*n for i in range(dataLen): self.update(self.aa[i],n) self.count += i+1-self.getSum(self.aa[i]) return self.count
完成提交后发现:

通过率才50%,分析原因才知道,树状数组中如果最大值远远大于数组的长度,就会造成很多空间的浪费,而当插入时调用update方法会依次去更新这些值,所以造成了空间的浪费,比如 需要排序的数的范围0-999999999,但是数组中只有1000个数字,这时候就需要对数据进行离散化,让数据靠的更近一下,比如 900 10 0 50 40 ------- 离散后aa数组就是 5 2 1 4 3
class Solution3:
aa = []
c = []
count = 0
nMax = 0
n = 0
def lowbit(self,x):
return x&-x
def getSum(self,n):
cSum = 0
while n>0:
cSum += self.c[n]
n -= self.lowbit(n)
if self.c[0]==1:
cSum += 1
return cSum
def update(self,i,n):
if i==0:
self.c[i] = 1
return
while i<n:
self.c[i] += 1
i += self.lowbit(i)
#离散化函数
def discretization(self,data):
b = sorted(data)
for i in range(len(data)):
self.aa[i] = b.index(data[i])
print(sys.getsizeof(b))
def findMaxNumber(self,data):
maxNumber = data[0]
for i in range(1,len(data)):
if maxNumber<data[i]:
maxNumber = data[i]
return maxNumber
def InversePairs(self,data):
dataLen = len(data)
self.nMax = self.findMaxNumber(data)
n = self.nMax+1
self.aa = data
self.c = [0]*n
for i in range(dataLen):
self.update(self.aa[i],n)
self.count += i+1-self.getSum(self.aa[i])
return self.count
这样,原本以为就万事大吉了,可没想到case通过率还是只有50% Σ(⊙▽⊙"a
STEP E 关于时间和空间复杂度的分析


 浙公网安备 33010602011771号
浙公网安备 33010602011771号