线性代数--矩阵 特征值特征向量
本章基调: A是n阶方阵
λ可以为0,特征向量不能为0
结论:
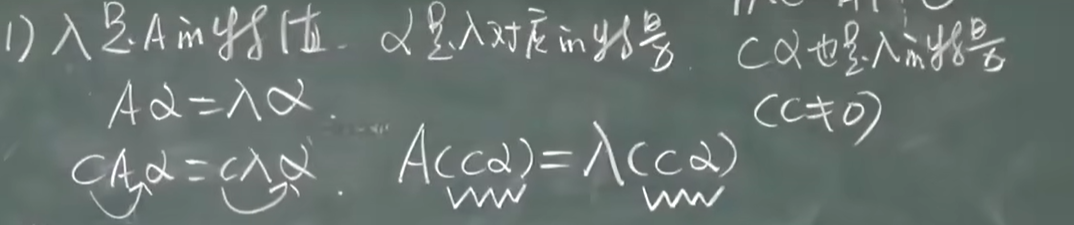
对应λ的特征向量不是唯一的
但是一个特征向量α只能对应一个特征值
2.
性质
- 主对角元素相加叫做迹tr(A)
A可逆的充要条件- A的行列式不等于0
- A的秩等于n 行秩列秩等于n 行向量列向量线性无关
- A的所有特征根都不等于0
- Ax = 0只有零解
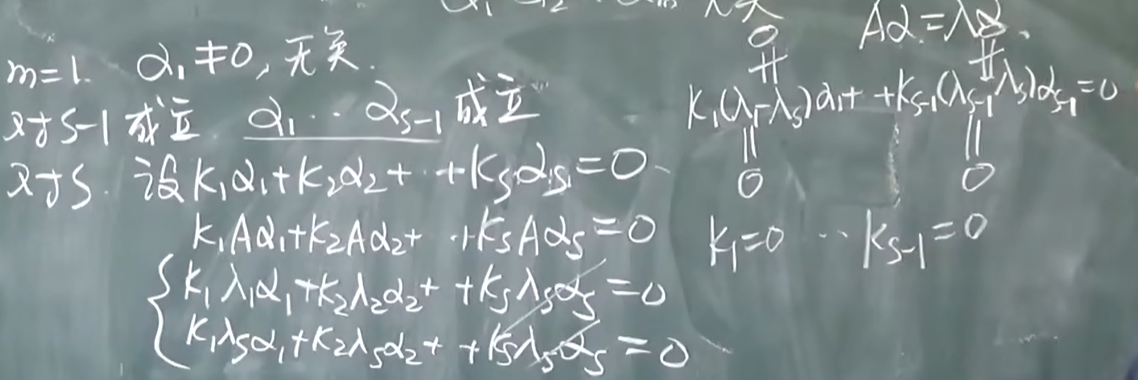
带入原式: 特征向量不能等于0
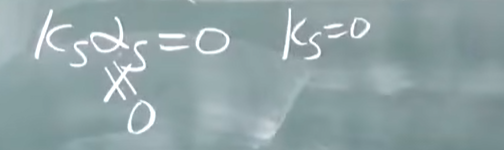
和上面性质的区别:一个特征值找一个特征向量 和 一个特征值对应于多个特征向量
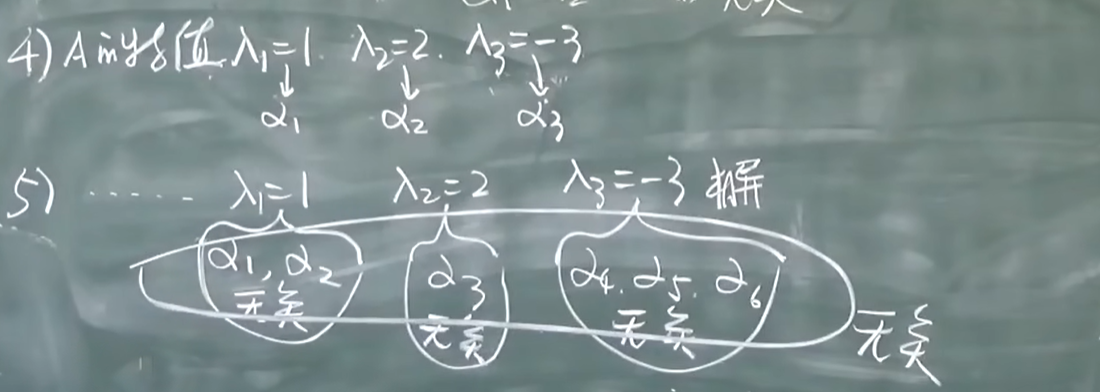
- k重特征根对应的线性无关的特征向量的个数小于等于k
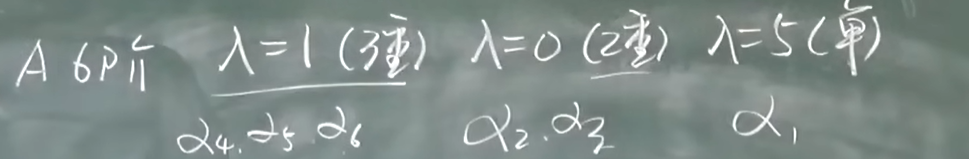
n阶矩阵A所有线性相关的向量的个数最多为n个
其他性质:
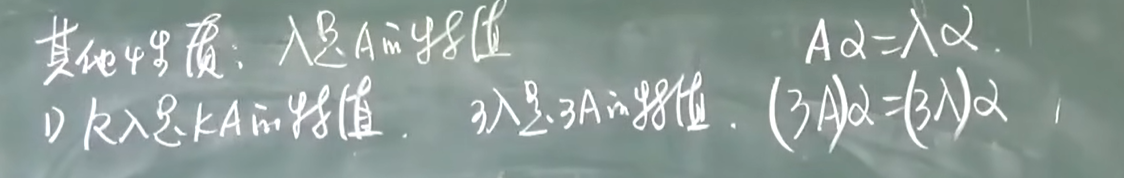
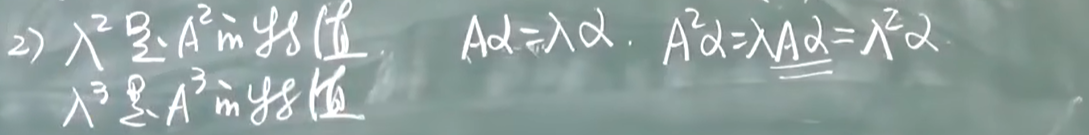
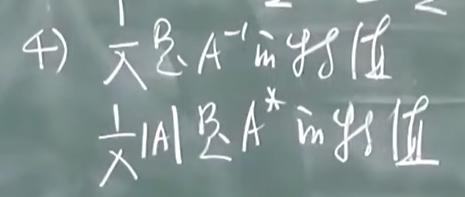
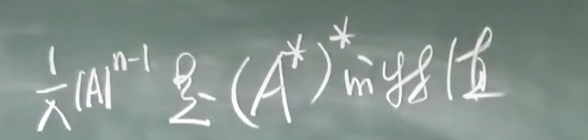
相似矩阵 可对角化条件
相似: AB是两个n阶方阵,存在n阶可逆矩阵p,使得
则A相似B
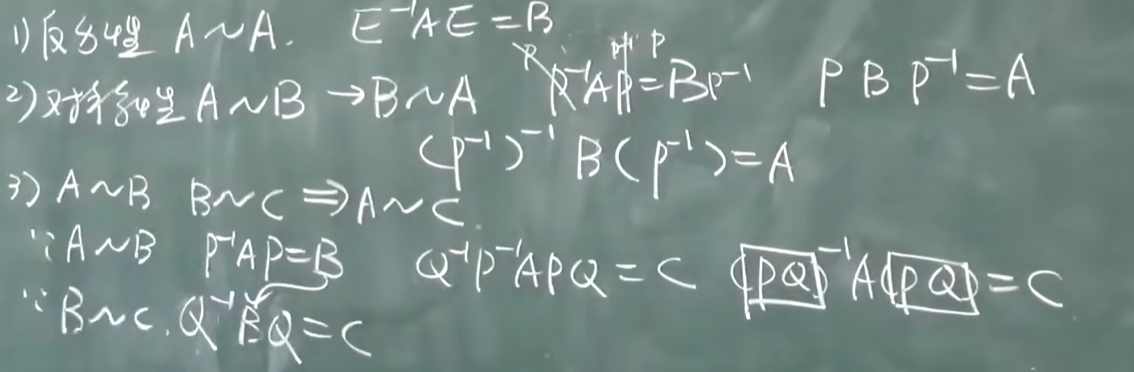
有相同的特征值 不一定 相似
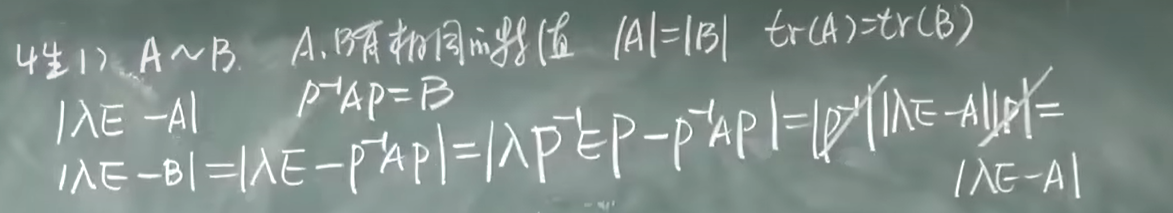

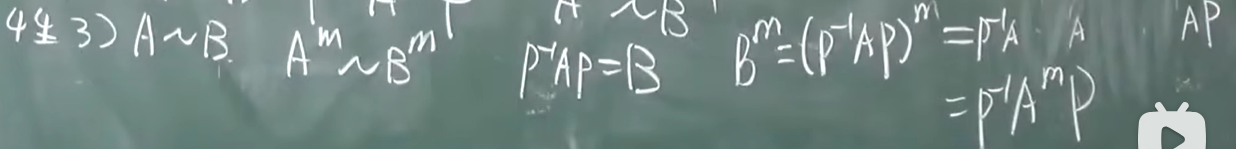
矩阵与对角型矩阵相似的条件
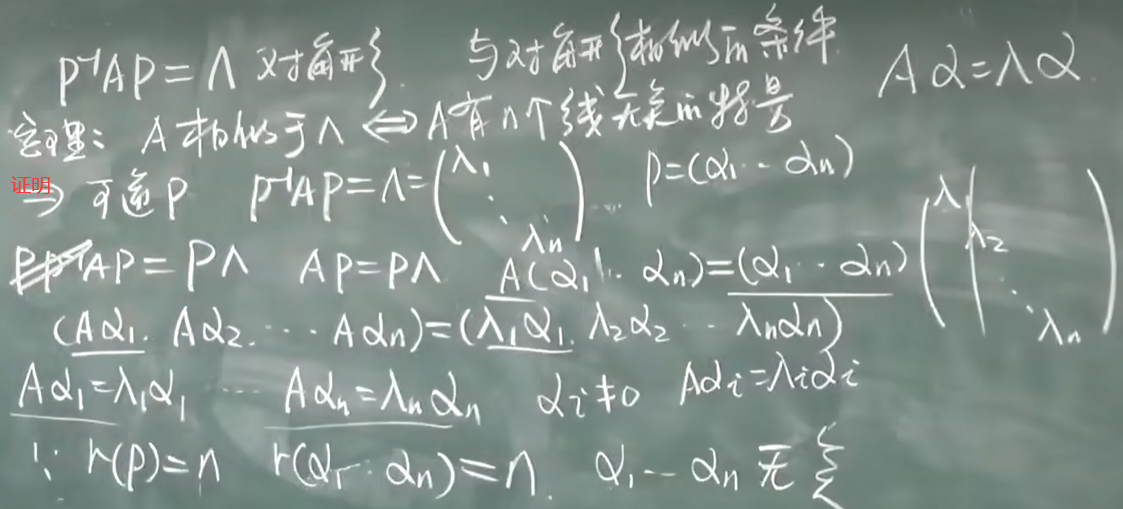
A有n个互异的特征根
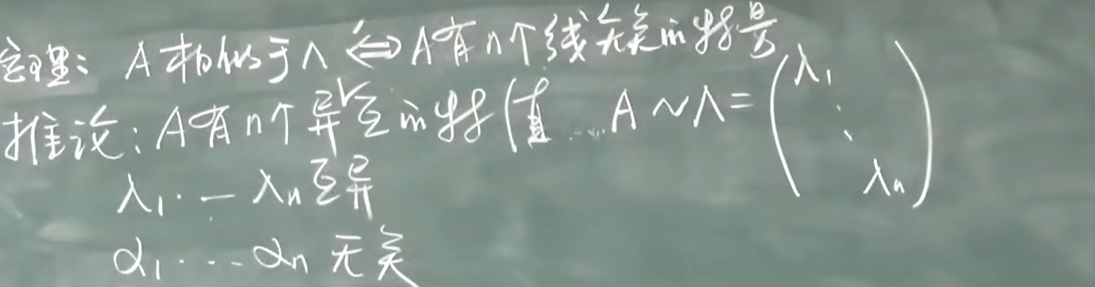
A的特征值都是单根: 一定相似于对角型
有重根:找重根的特征向量的个数 = 重数 才能相似于对角型
求相似解题步骤:
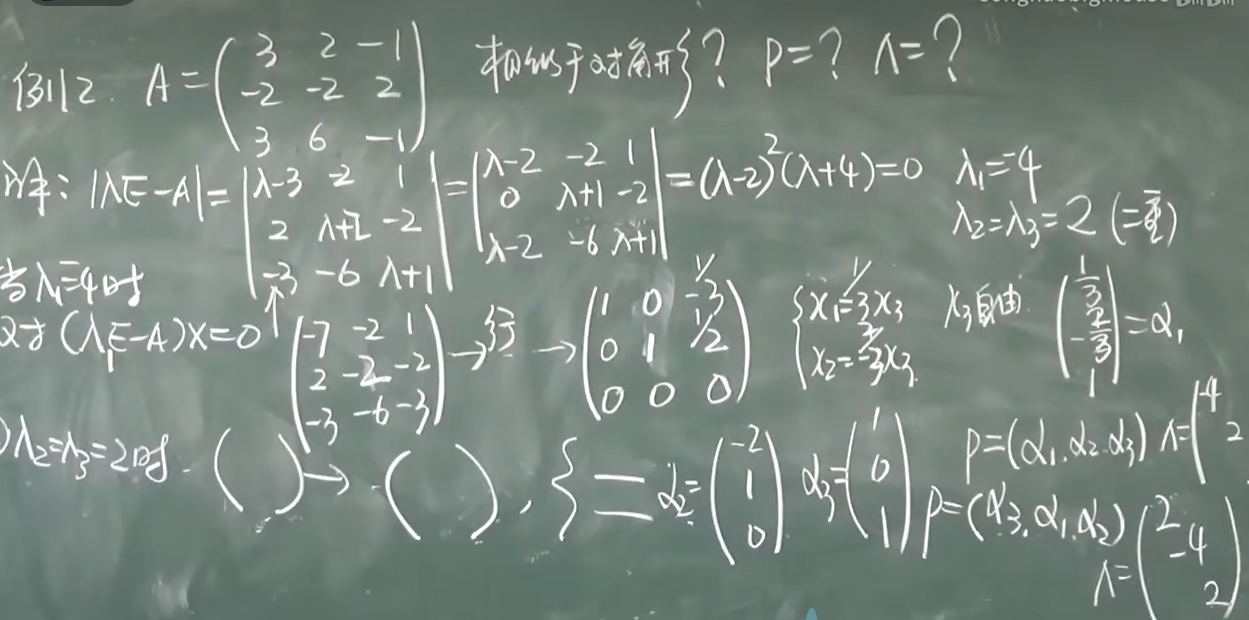
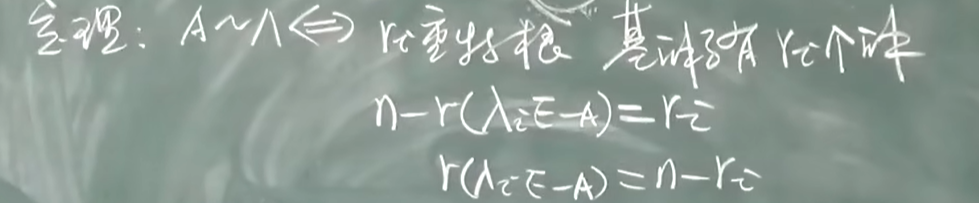
求高次方很方便
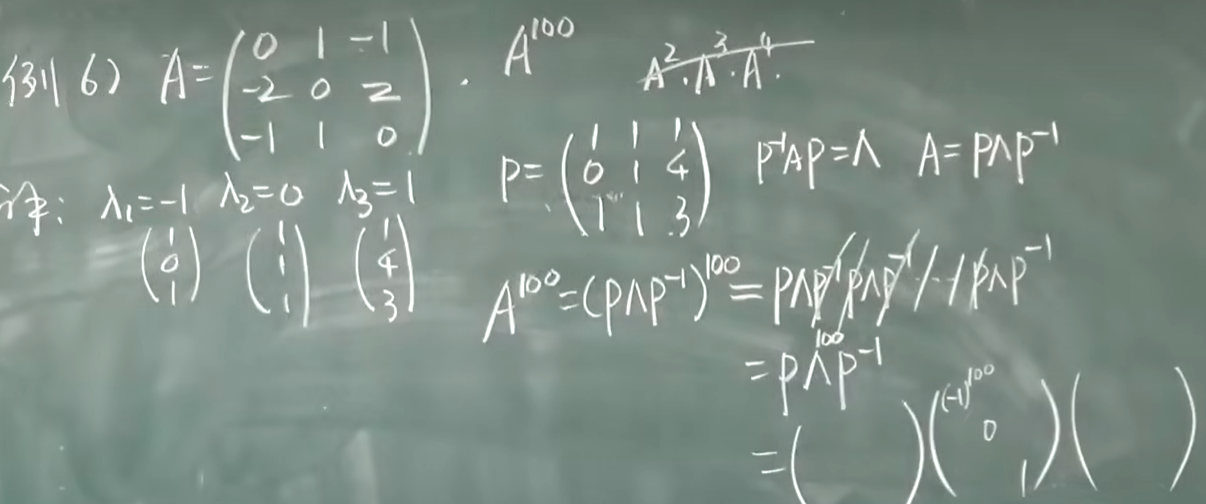
实对称矩阵的对角化
所有的实对称矩阵都能对角化
- 定理:
- 实对称A的不同特征值对应的特征向量一定正交
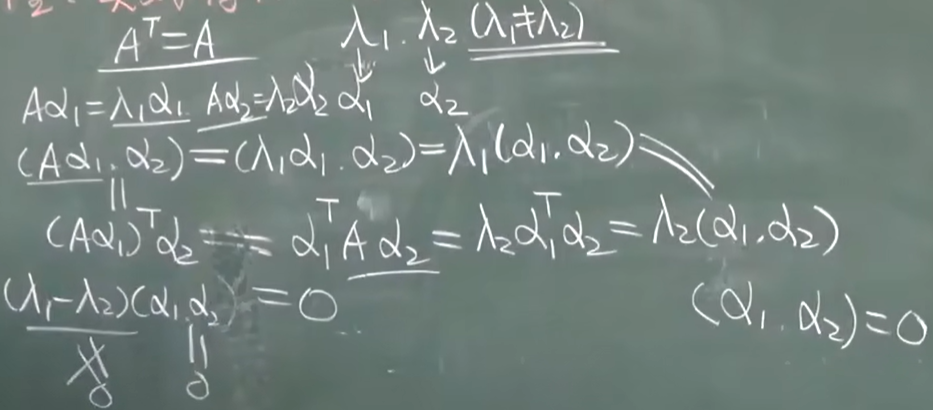
内积
向量分量相乘再相加,内积是个数
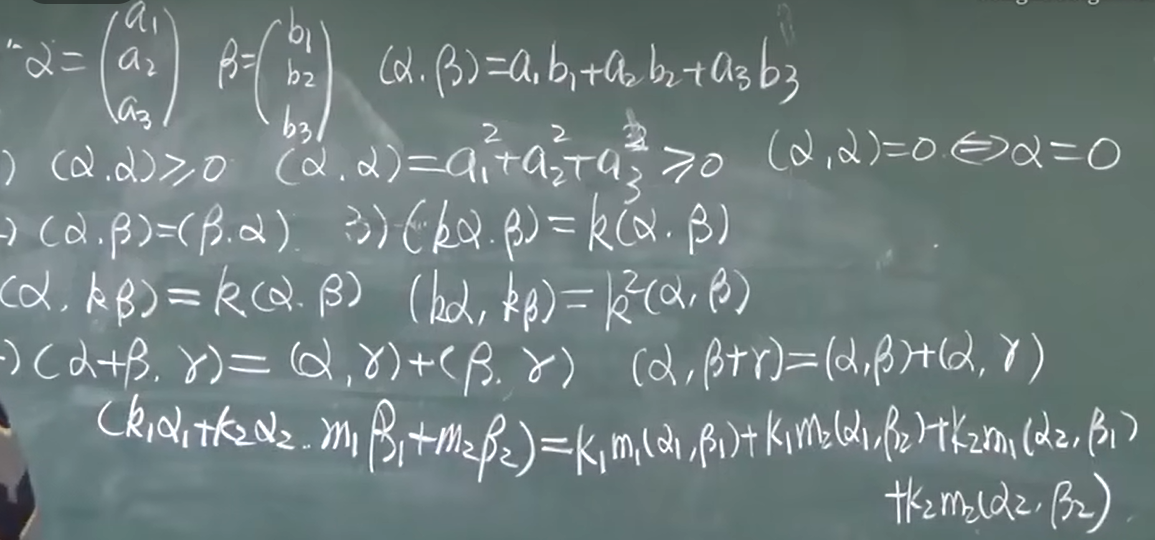
向量的长度(范数, 模)
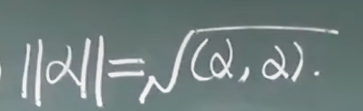
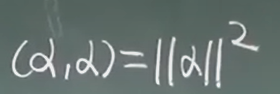
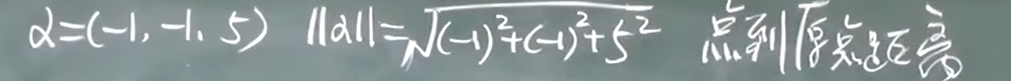
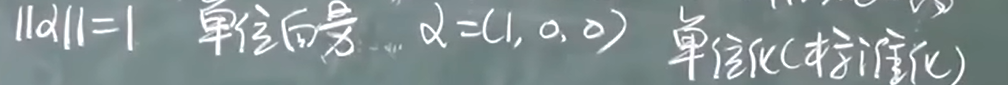
- 长度的性质:
- 三角形公式:
正交(垂直)
两个向量做内积等于0 记为:
- 显然零向量与任何向量都正交
- 和自身正交的向量只能是零向量
正交向量组(不含零向量的向量组)
一组向量两两都正交
每个向量长度都是1, 叫做标准正交向量组
定理:
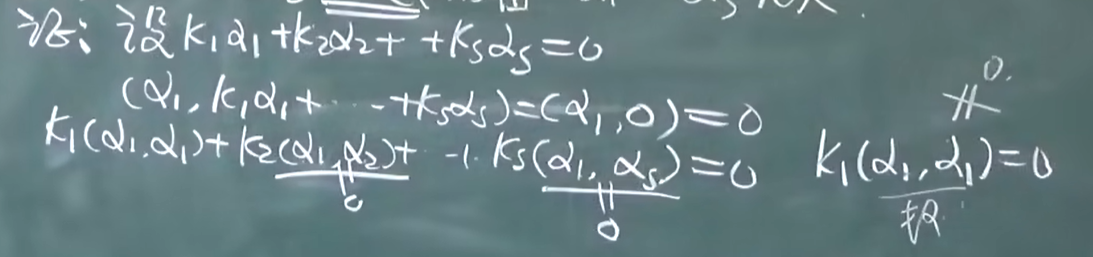
施密特正交化
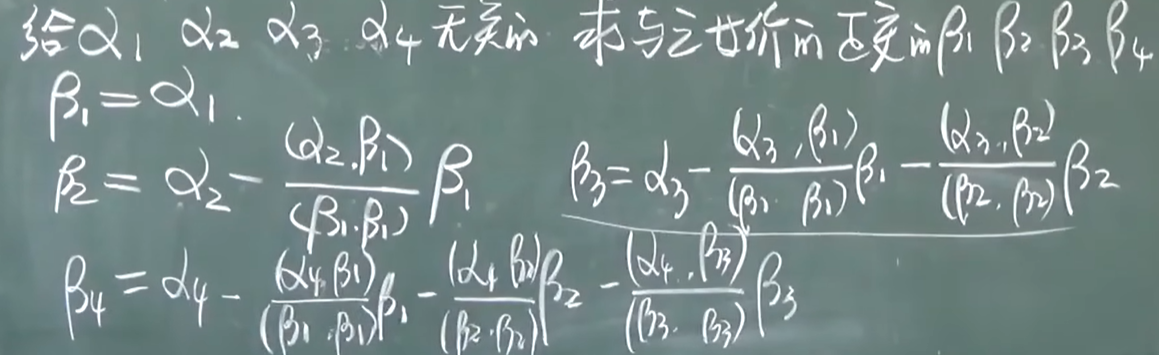
单位化:
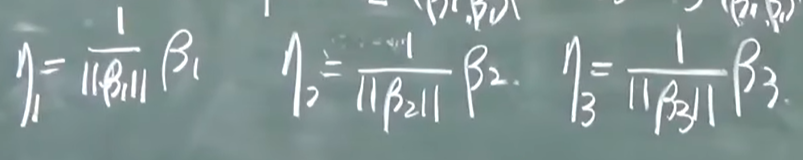
正交矩阵
A是n阶方阵,
- 性质:
-
如果A是正交矩阵,A的行列式=-1 or 1
-
如果A是正交矩阵,A逆=A转置,且A逆和A转置均为正交矩阵
-
如果A,B都是n阶正交矩阵那么AB也正交
- 定理
正交相似一定相似
AB是同阶方阵,存在正交矩阵P,使得
A实对称矩阵,一定存在正交矩阵Q,使得
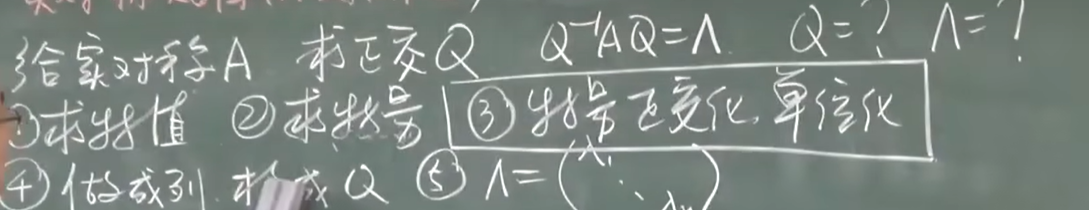


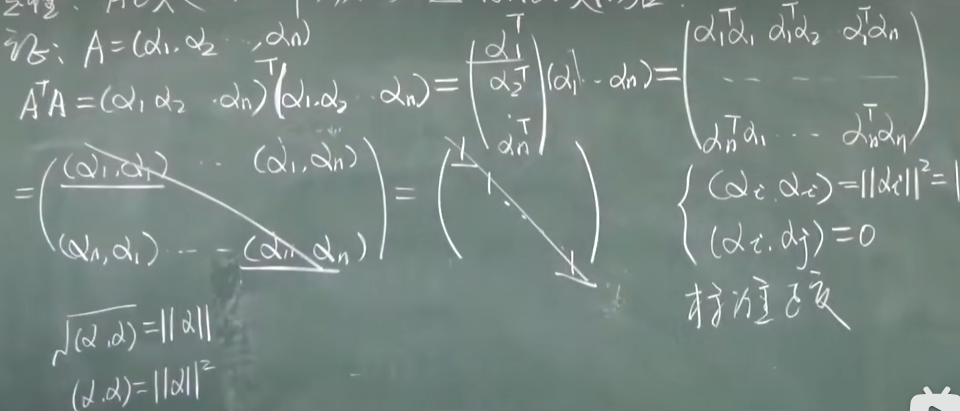


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通
2023-10-25 闭包