线性代数--向量
向量
n个数a1 a2 ...... an组成的有序数组(a1 a2 ... ... an) a1..又称为分量 维数
- 行向量
- 列向量
只是形式不同 - 零向量
分量全是0 - 负向量
相反数 - 两个向量相等
同维向量 - 向量相加减
k是数 另一个是向量
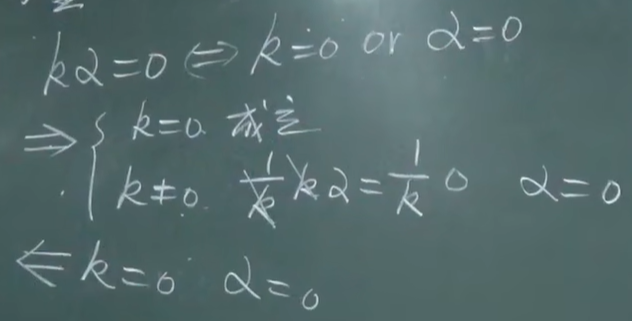
向量间的线性关系
线性关系:用某些向量能表示一个向量
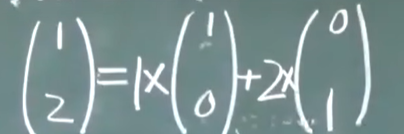
线性组合:
线性组合转化成方程组是否有解? 能不能找到一组系数满足上式

- 零向量可由任意向量组来表示
- 向量组中的任意向量可有向量组表示
- 任意向量都可由
来表示 又称n维单位向量组
向量组等价
两个向量组是同维的,可以相互表示
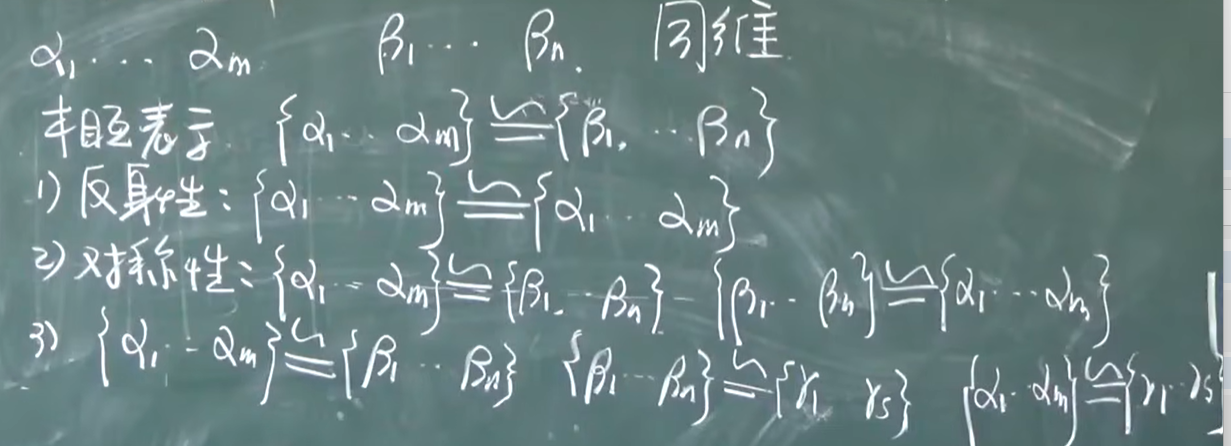
线性相关与线性无关

无关:
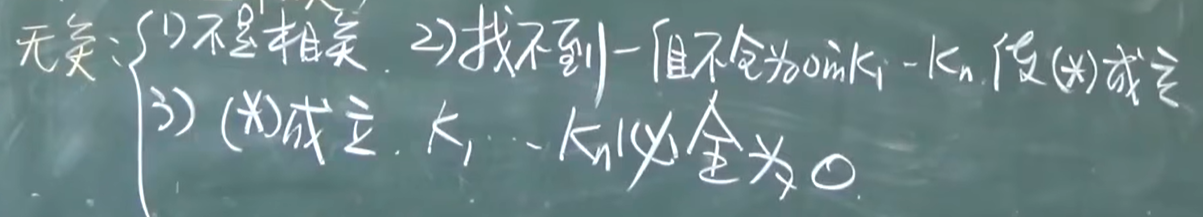
-
向量组中两向量成比例 相关
-
含有零向量的任意向量组 相关
-
一个零向量必线性相关
-
任意一个非零向量必线性无关
-

-

部分组线性相关,整体组也线性相关
逆否命题:
整体组线性无关推出部分组线性无关 -
线性无关的向量组,接长向量组也线性无关
线性相关的向量组,截短向量组也线性相关

-
向量的个数等于向量的维数才能用
n个n维向量
D不等于0的充要条件线性无关
D等于0的充要条件线性相关 -
n维单位向量组 线性无关
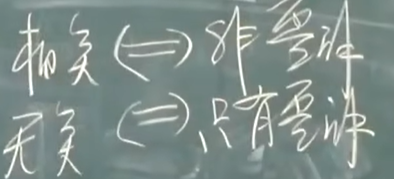

- 线性组合和线性相关定理
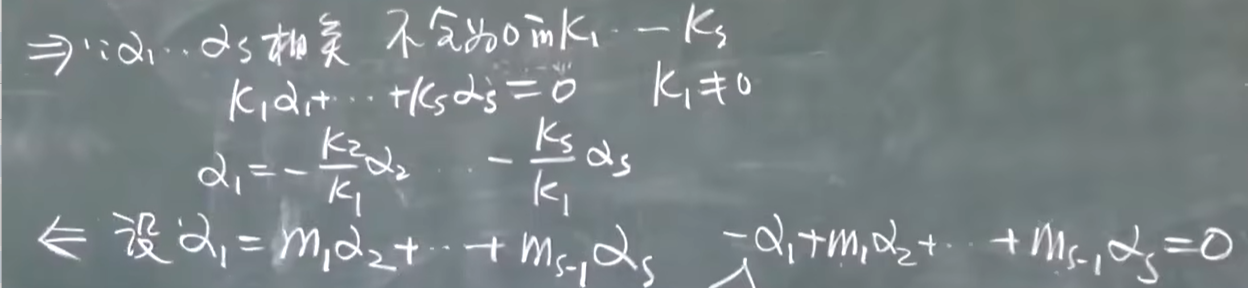
证明可表示:
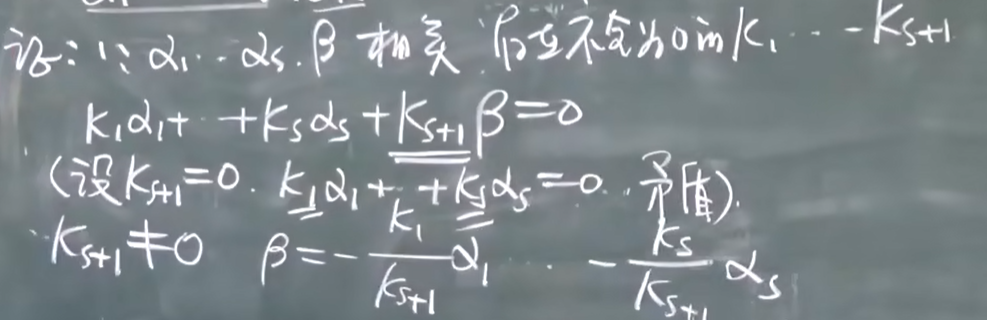
证明唯一性:
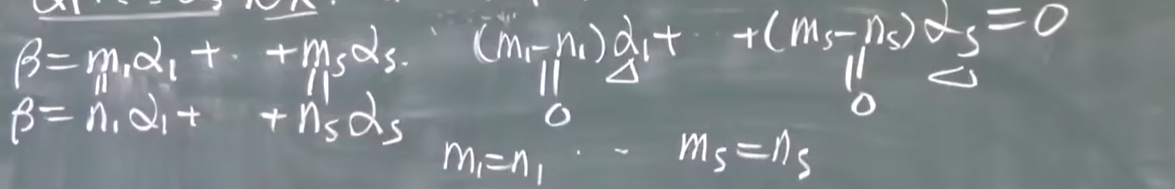
- 替换
逆否命题:
- m > n,m个n维向量相关 向量个数>向量维数时, 一定是线性相关
n+1个n维向量线性相关
推论: 两个等价的线性无关组,含向量个数时相同的
向量组的秩
极大线性无关组含有向量的个数
- 极大线性无关组:可以不唯一,但是含有向量的个数一样多
定理:

- 向量组α1,α2线性无关
- 极大:找线性无关的向量组的向量个数是最大的
性质
- 向量组α1,α2线性无关
- 任意r+1个变量都是线性相关的
全是零向量:秩=0
注:n+1个n维向量线性无关
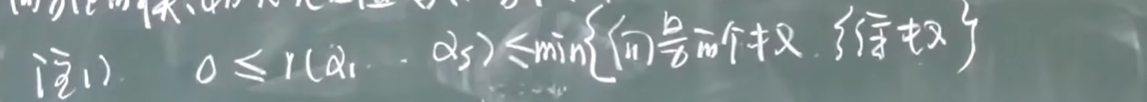
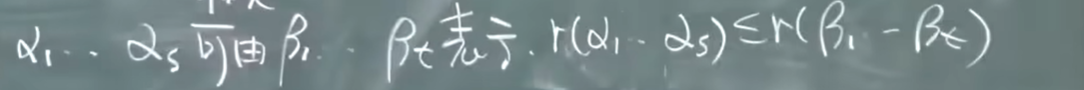
- 若两个向量组等价, 秩相等
矩阵的行秩和列秩
- 定理:
- 矩阵的行秩 === 列秩 === 矩阵的秩
- r(AB) <= min
- 对矩阵A仅作初等行变换,化成矩阵B,那么矩阵A的列向量组同矩阵B的列向量组有完全相同的线性关系
简述--初等行变换不改变矩阵列向量的线性关系
线性关系:线性无关,相关,线性表示


