线性代数--矩阵
矩阵
- 代表一张树表
- m*n 行数不一定等于列数
- 同型矩阵 有前提:AB行数相等 列数相等
- 矩阵相等 同型矩阵并且对应的元素相等
- 零矩阵 所有元素均为0
两个零矩阵一定相等是错误的:矩阵相等的前提是同型矩阵
特殊矩阵
- 方阵: 行数===列数 也有主对角线和副对角线
一行一列: - 负矩阵 方阵
所有元素都取相反数 - 上三角形矩阵,不能这样写。方阵
![image]()
- 下三角形矩阵 方阵
- 对角型矩阵 方阵
- 数量矩阵 方阵
主对角元素全是一样,特殊的对角型矩阵 - 单位阵 方阵
主对角元素全是1
矩阵的加减法
- 对应的元素相加减,有前提条件,必须要为同型矩阵
- 运算规律:
- A + B = B + A
- (A + B) + C = A + (B + C)
- A + 0 = A 0为零矩阵 必须为同型矩阵
- A +(-A)= 0
- A - B = A +(-B)
- A + B = C A = C - B
矩阵的数乘
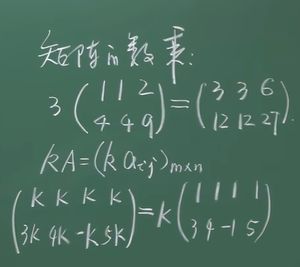
- 矩阵提公因子:矩阵的所有元素均有公因子k,k向外提一次
- 行列式提公因子:
- 行列式的某一行有公因子k,k向外提一次
- 行列式的所有元素均有公因子k,k往外提n次
- 运算规律 K,L是数
- K(A + B) =KA + KB
- (K + L) A = KA + LA
- (kL)A = k(LA) = L(kA)
- 1 * A = A
- -1 * A = -A
矩阵的乘法
"中间相等,取两头"
- 两个矩阵做乘法的前提条件
第一个矩阵的列数=第二个矩阵的行数 - 结果矩阵的形状
结果矩阵的行数=第一个矩阵的行数
结果矩阵的列数=第二个矩阵的列数 - 乘法不满足
- 不满足交换律 AB
一般 不等于 BA,AB有意义时,BA不一定有意义
![image]()
- 不满足消去律 AB = AC 且A不等于0 推不出B===C
![image]()
- AB = 0 推不出 A=0 或 B=0
- 左乘右乘,不能搞反,有问题
![image]()
- 矩阵乘法满足
- 结合律 (AB)C = A(BC)
- 分配律 A(B+C)= AB + AC (B+C)A= BA + CA
- k(AB) = (kA)B = A(kB)
- AE = EA = A
- AO = OA = O O是零矩阵
- 对角型
矩阵可交换的 AB= BA
- AB是同阶方阵
- 不是同阶方阵 一定不可交换
- AB BA不相等 不可交换
- E任何同阶方阵均可交换 EA = AE = A
- 同阶的对角阵也可交换
方阵的幂 只有方阵才能求
- 性质
- 公式
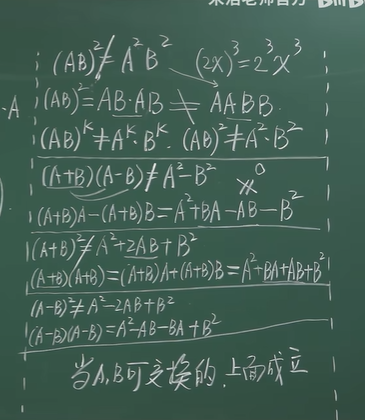
2. 二次公式
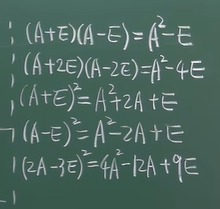
3. 三次公式
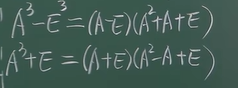
4. 十字
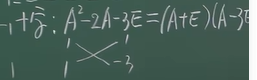
例1:
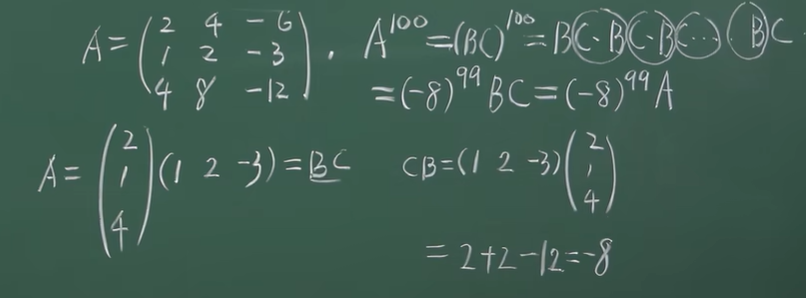
矩阵的转置
- 性质
对称矩阵和反对称矩阵
奇数阶反对称行列式等于0
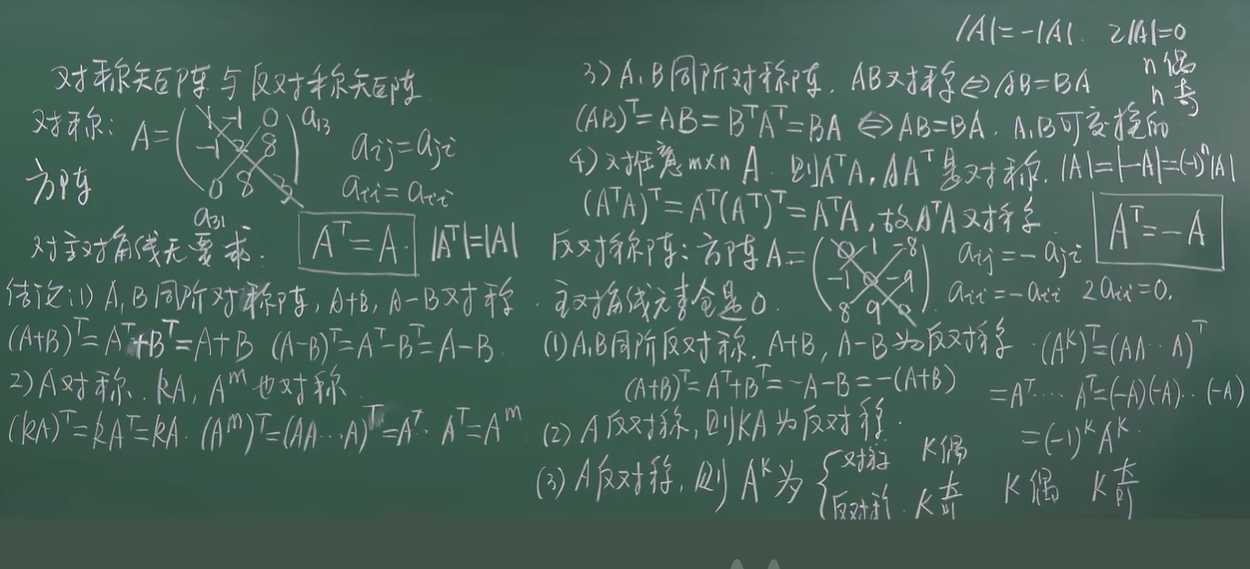
方阵的行列式 只有方阵才有行列式
- 性质:
伴随矩阵 只有方阵才能求伴随矩阵
按行求的代数余子式按列放
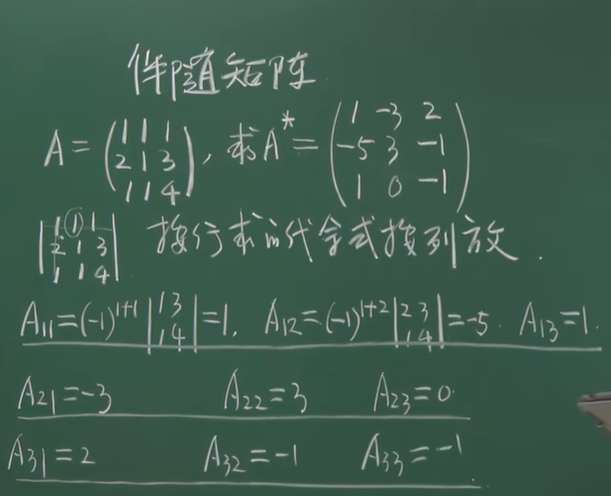
- 性质
-
任何时候都成立
![image]()
-
![image]()
![image]()
-
![image]()
-
![image]()
逆矩阵
设A为n阶方阵,若存在n阶方阵B,使AB = BA = E
A是可逆阵,
- 只有方阵,有资格讨论可逆,不可逆
- 若A可逆,逆阵是唯一的
- 未必所有方阵都可逆
- 非奇异-可逆-满秩-非退化
奇异-不可逆-降秩-退化
![image]()
- 怎么判断A可逆不可逆?
- A可逆,逆矩阵怎么求?
![image]()
- 推论:
A B是n阶方阵,若AB=E(或BA=E)
则A可逆且 - 性质
![image]()
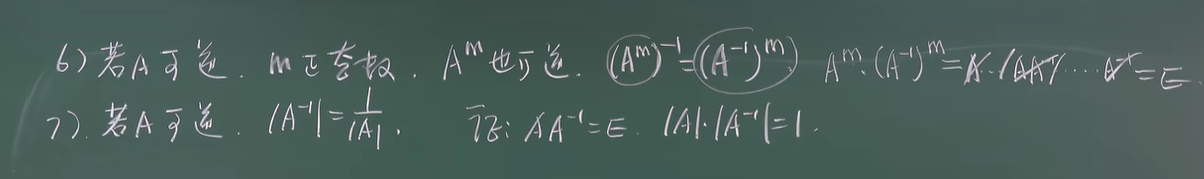
矩阵方程
初等变换
- 行/列, 用箭头连接
- 交换两行/列
- 非零数乘以某一行/列
- 某一行/列的L倍加到另一行/列上去
标准型
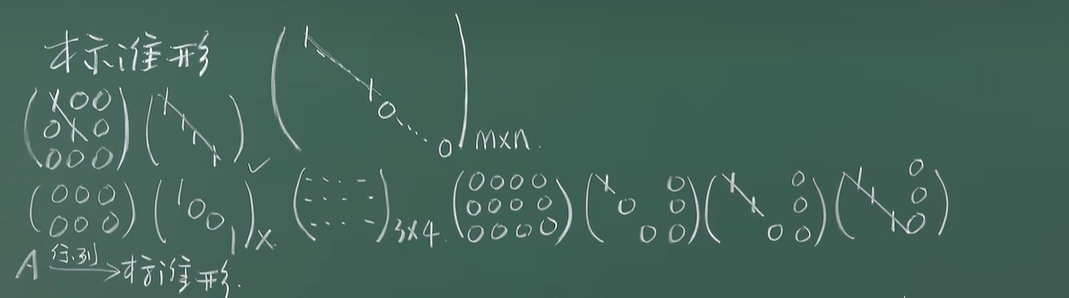
行阶梯型矩阵
- 如果有0行, 0行都在非零行的下面
- 非0行的首非0元的左下方的元素(若有的话)全是0
![image]()
画的要点: 竖线只过一个数,横线可过多个数
行简化阶梯型
- 必须先是阶梯型
- 非0行的首非零元必须都是1
- 非0行的首非零元所在的列,除了它自己,其他元素必须都是0
![image]()
任何的矩阵A都可以经过初等变换化成阶梯型,然后做初等行变换变为行简化阶梯型
- 阶梯型不唯一
- 如果只做初等行变化,行简化阶梯型是唯一的
初等矩阵 方阵
- 由单位阵E做一次初等变换(行,列)得到的矩阵,三种变换
性质:
- 初等矩阵的行列式不为0
- 初阵的转置阵仍是同类型的初阵
- 初等矩阵均可逆,其逆矩阵也是同种类型的初等矩阵
![image]()
![image]()
- A做一次行变换,相当于同种的初等矩阵左乘A
A做一次列变换,相当于同种的初等矩阵右乘A - 推论: A,B等价的充要条件存在可逆PQ PAQ = B
等价:矩阵A通过初等变换得B
A可逆的充要条件A的标准型为E
A可逆的充要条件表示为初等矩阵的乘积
求逆矩阵的方法:初等行变换法 (只做行变换)
![image]()
注:不管是否可逆,如左边化不成E,说明原来A不可逆
矩阵的秩
- 秩: 非零子式的最高阶数
![image]()
- 求秩
充要条件: r(A) = 0 有一个r阶子式不为0,而所有的r+1阶全为0
- 阶梯型矩阵的秩:非零元行的行数
- 初等变换(行列)不改变矩阵的秩
- 性质
![image]()

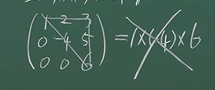
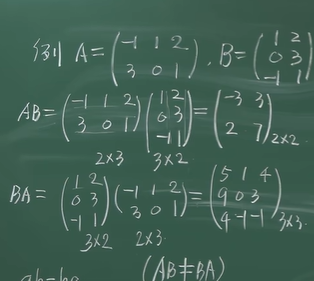
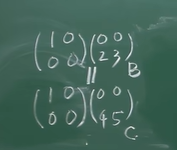

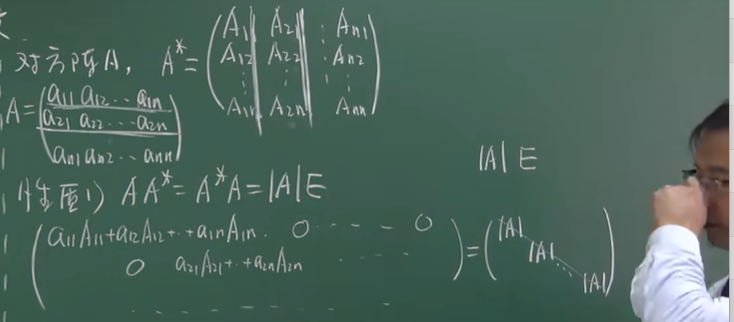

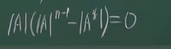
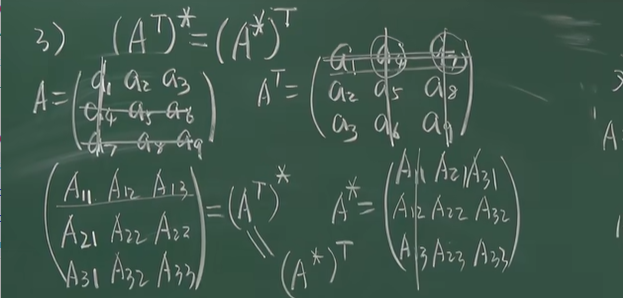
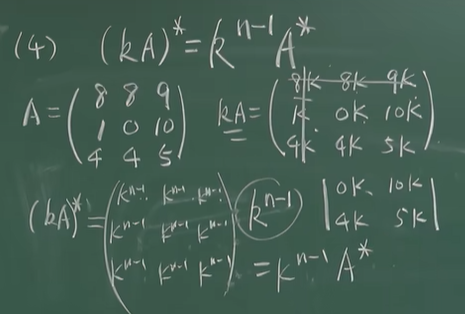

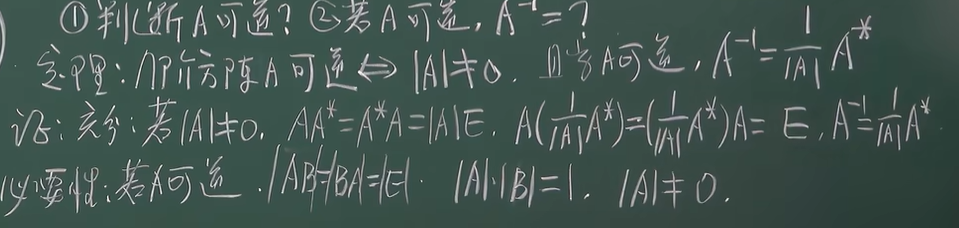
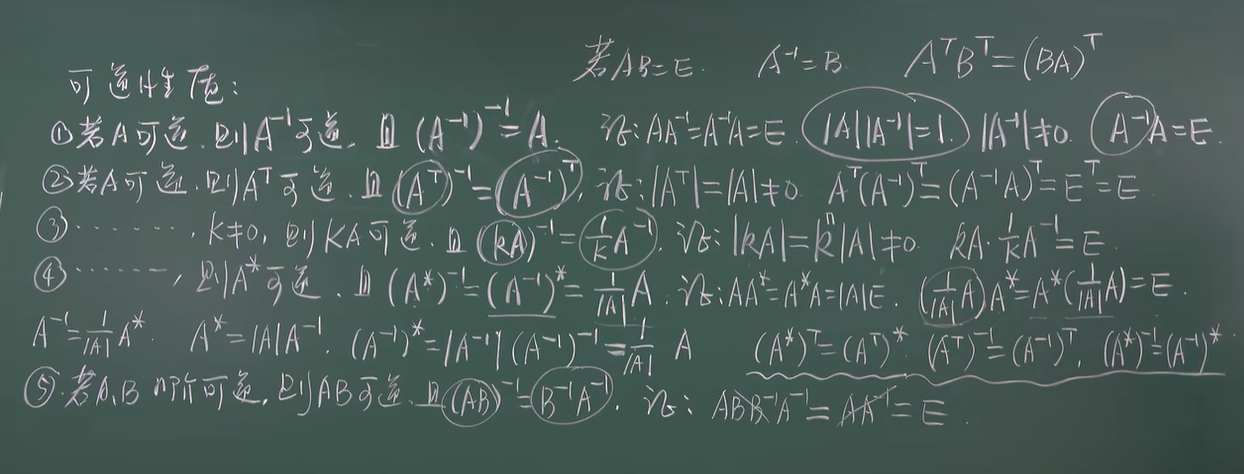

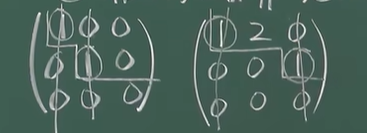
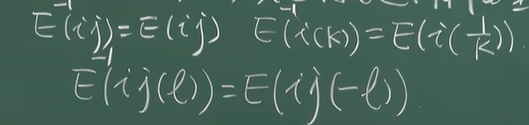
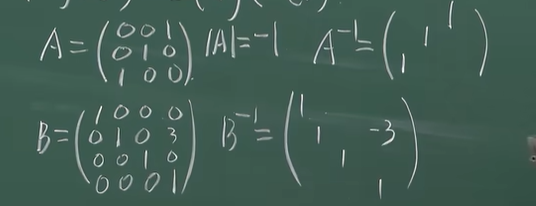


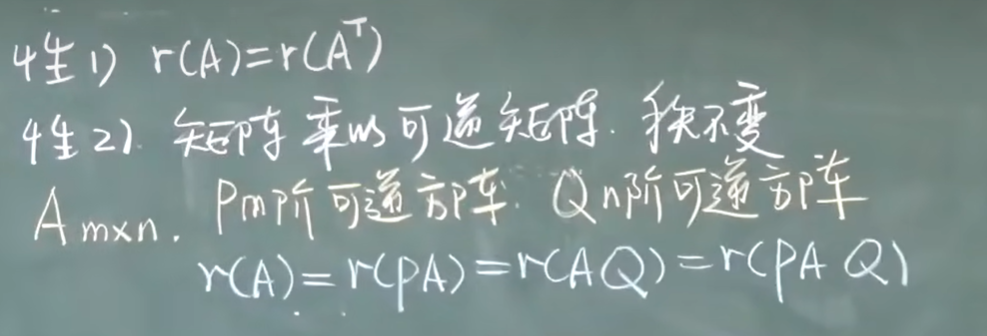

 浙公网安备 33010602011771号
浙公网安备 33010602011771号