转载https://www.luogu.org/problemnew/solution/P1665，http://bailian.openjudge.cn/practice/2002/的新解法

不知道为什么O(n^4)O(n4)的玄学方法能过，正解显然是O(n^2)O(n2)的，枚举对角线，然后算出另外两点判断存不存在。

关键就在怎么通过对角线算出另外两点的坐标。

先贴公式。

int midx = (x[i] + x[j]) / 2;
int midy = (y[i] + y[j]) / 2;            
int x1 = midx - (midy - y[i]), y1 = midy + (midx - x[i]);
int x2 = midx + (midy - y[i]), y2 = midy - (midx - x[i]);

(x[i],y[i]),(x[j],y[j])(x[i],y[i]),(x[j],y[j])是对角线的两个点，

(x1,y1),(x2,y2)(x1,y1),(x2,y2)是我们算出来的另两个点的坐标。

怎么来的呢？

如图，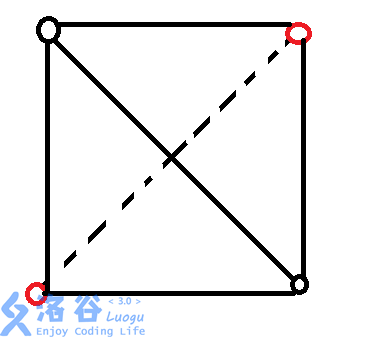 

黑点是我们枚举的对角线，红点就是我们要算的另外两点。

我们算出对角线的重点(midx,midy)(midx,midy)。

然后做几条辅助线，如图：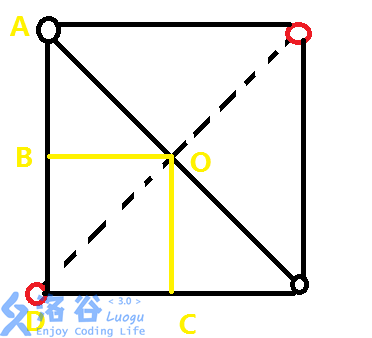 

图中的OCOC,OBOB是垂直于xx轴和yy轴，并不一定垂直于正方形的边。

易得△ABOABO ≌ △DCODCO，于是，这两个三角形以ABAB,CDCD为底的高也相等，现在是不是就能理解这个公式了。

贴代码O(n^2)O(n2)常数小

#include <cstdio>
#define Open(s) freopen(s".in","r",stdin);freopen(s".out","w",stdout);
#define Close fclose(stdin);fclose(stdout);
int n, ans;
int x[60000], y[60000], vis[1100][1100], xs[1100][1100];
int main(){
    Open("count");
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i){
        scanf("%d%d", &x[i], &y[i]);
        x[i] = (x[i] + 51) << 1; //防止负数和小数
        y[i] = (y[i] + 51) << 1;
        vis[x[i]][y[i]] = 1;
    }
    for(int i = 1; i < n; ++i)
        for(int j = i + 1; j <= n; ++j){
            int midx = (x[i] + x[j]) / 2;
            int midy = (y[i] + y[j]) / 2;            
            int x1 = midx - (midy - y[i]), y1 = midy + (midx - x[i]);
            int x2 = midx + (midy - y[i]), y2 = midy - (midx - x[i]);
            if(x1 <= 0) continue; if(x2 <= 0) continue;
            if(y1 <= 0) continue; if(y2 <= 0) continue; 
            if(vis[x1][y1] && vis[x2][y2]) ++ans;
        }
    printf("%d\n", ans >> 1);
    return 0;
}