POJ-2142 The Balance 扩展欧几里德（+绝对值和最小化）

题目链接：https://cn.vjudge.net/problem/POJ-2142

题意

自己看题吧，懒得解释

思路

第一部分就是扩展欧几里德
接下来是根据 $ x=x_0+kb', y=y_0-ka' $
其中 $ a'=\frac{a}{gcd(a, b)}, b'=\frac{b}{gcd(a, b)} \( 来最下化这两个式子： \) |x|+|y| \( \) |ax|+|by| $

那么回想高中不等式的学习，我们可以通过画图来解决这个最小化问题

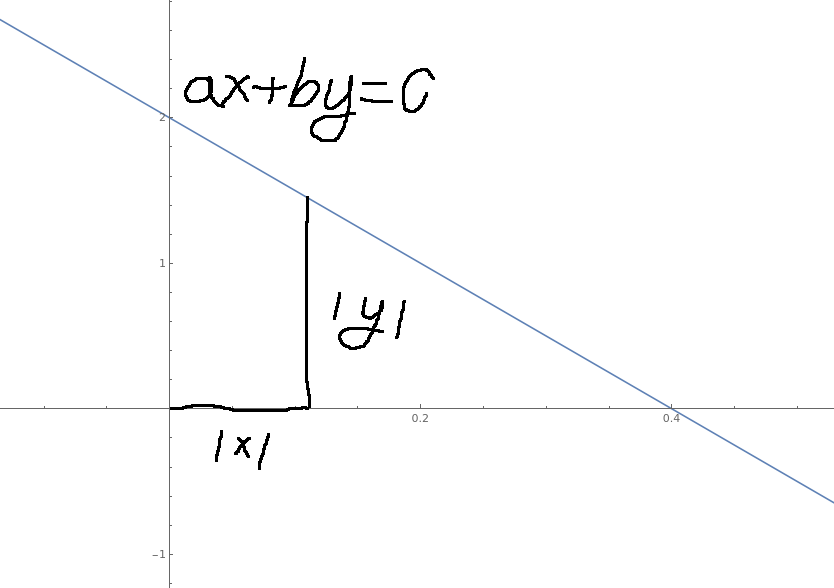
可以发现在$ x<0 $或 $ y<0 $的情况下，曼哈顿距离递增，那么绝对值和的最小值就存在与轴的附近

代码

#include <cstdio>
#define abs(x) (((x)>0)?(x):(-x))
void exgcd(int a, int b, int &d, int &x, int &y){
    if (b==0) {d=a; x=1; y=0;}
    else {exgcd(b, a%b, d, y, x); y-=x*(a/b);}
}

int main(void){
    int a, b, c;

    while (scanf("%d%d%d", &a, &b, &c)==3 && a){
        int x, y, d;
        exgcd(a, b, d, x, y);
        a/=d; b/=d; c/=d;
        x*=c; y*=c;
        
        int ax, ay, bx, by;
        ax=(x%b+b)%b;
        ay=(c-a*ax)/b;
        by=(y%a+a)%a;
        bx=(c-b*by)/a;
        // printf("%d %d||%d %d||%d %d\n", x, y, ax, ay, bx, by);

        if (abs(ax)+abs(ay)<abs(by)+abs(bx))
            printf("%d %d\n", abs(ax), abs(ay));
        else if (abs(ax)+abs(ay)>abs(by)+abs(bx))
            printf("%d %d\n", abs(bx), abs(by));
        else if (a*abs(ax)+b*abs(ay)>b*abs(by)+a*abs(bx))
            printf("%d %d\n", abs(bx), abs(by));
        else printf("%d %d\n", abs(ax), abs(ay));
    }

    return 0;
}

Time	Memory	Length	Lang	Submitted
None	132kB	930	C++	2018-05-12 23:56:52