动态规划-01 背包问题

题目

一共有N件物品，第i（i从1开始）件物品的重量为w[i]，价值为v[i]。在总重量不超过背包承载上限W的情况下，能够装入背包的最大价值是多少

方法

动态规划公式

dp[i][j] = max(dp[i−1][j], dp[i−1][j−w[i]]+v[i])

该公式主要是讲问题分解为一个个的小问题 然后求出最优解

样例

苹果价值1元，重1kg，桃子价值2元，重2kg，西瓜价值5元，重4kg，求可容纳6kg背包可拥有的最大价值

解法

构建矩阵

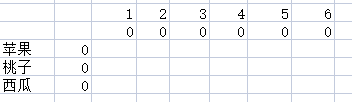
列 代表背包的价值
行 代表可容纳的物品，每一行可以拥有上一行的物品

0 只是为了方便计算

公式解析

dp[i−1][j] 代表不含有此物品时拥有的最大价值

dp[i−1][j−w[i]]+v[i] 代表拥有此物品时的最大价值，v[i]代表当前物品的价值，j−w[i]代表装了当前物品后剩余的容量

取这两者的最大值

01 背包问题的变种

王强决定把年终奖用于购物，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：
主件 附件
电脑 打印机，扫描仪
书柜 图书
书桌 台灯，文具
工作椅 无
如果要买归类为附件的物品，必须先买该附件所属的主件，且每件物品只能购买一次。
每个主件可以有 0 个、 1 个或 2 个附件。附件不再有从属于自己的附件。

请你帮助王强计算可获得的最大的满意度

解法

与背包问题类似，唯一不同点 是 当遇到物品是附件是 取dp[i−1][j]，当时主件时，取 dp[i−1][j] ， 不含附件，含有附件 的最大值