MNIST手写数字识别:分类应用入门(理论篇)
慕课:《深度学习应用开发-TensorFlow实践》
章节:第七讲 MNIST手写数字识别:分类应用入门
TensorFlow版本为2.3
MNIST手写数字识别数据集介绍及获取
MNIST 数据集来自美国国家标准与技术研究所, National Institute of Standards and Technology (NIST)。数据集由来自 250 个不同人手写的数字构成, 其中 50% 是高中学生, 50% 来自人口
普查局 (the Census Bureau) 的工作人员。
这一份数据集共有训练集60000个,测试集10000个,下面这张图展示了一小部分

数据集的获取可以直接去网站下:https://s3.amazonaws.com/img-datasets/mnist.npz
当然也可以通过TensorFlow的代码去获取数据集,不过值得注意的是,TensorFlow1.*和TensorFlow2.*的数据集获取方式并不相同,下面只提供TensorFlow2.*的获取代码
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
tf.__version__
#加载数据集
mnist=tf.keras.datasets.mnist
(train_images,train_labels),(test_images,test_labels)=mnist.load_data()
然后他就会去对应的网站上下载对应的数据集,不过有个问题,他的下载地址是对应谷歌的一个地址,因此有可能会出现下载错误或者下载失败或者下载比较的慢,还是建议去上面提供的那个链接下,当然如果有某些方式,那随意哈
如果你选择手动下载,那么请把下载的数据集mnist.npz存放在用户目录的“.keras/dataset”子目录下(Windows 下用户目录为 C:\Users\用户名 ,Linux 下用户目录为 /home/用户名 )。如果是第一次运行(在用户目录下没有找到数据文件),则会自动先从网络下载后再加载。如果用户目录下已经存在数据文件,则直接加载。
可以来看一下这一个数据集的一些信息
print(f"Train image shape:{train_images.shape} Train label shape:{train_labels.shape}");
print(f"Test image shape:{test_images.shape} Test label shape:{test_labels.shape}");

可以看到,他是28*28的一个黑白图片,也就是一张图片会有784个像素点。
可以用matplotlib.pyplot来看一下他的一个图像
def plot_image(image):
plt.imshow(image.reshape(28,28),cmap='binary')
plt.show()
plot_image(train_images[0])
去第一张图片看一下就长上面这个样子
逻辑回归
许多问题的预测结果是一个在连续空间的数值,比如房价预测问题,可以用线性模型来描述: 𝑌 = 𝑥1 ∗ 𝑤1 + 𝑥2 ∗ 𝑤2 + ⋯ + 𝑥𝑛 ∗ 𝑤𝑛 + 𝑏
但也有很多场景需要输出的是概率估算值,例如:
- 根据邮件内容判断是垃圾邮件的可能性
- 根据医学影像判断肿瘤是恶性的可能性
- 手写数字分别是 0、1、2、3、4、5、6、7、8、9的可能性(概率)
这时需要将预测输出值控制在 [0,1]区间内,二元分类问题的目标是正确预测两个可能的标签中的一个,逻辑回归(Logistic Regression) 可以用于处理这类问题。下图展示了逻辑回归的基本模型

在这个过程中,我们要确保输出值始终落在0和1直接,这里我们就需要用到Sigmoid函数
Sigmoid函数
Sigmoid函数(S型函数)其定义如下:
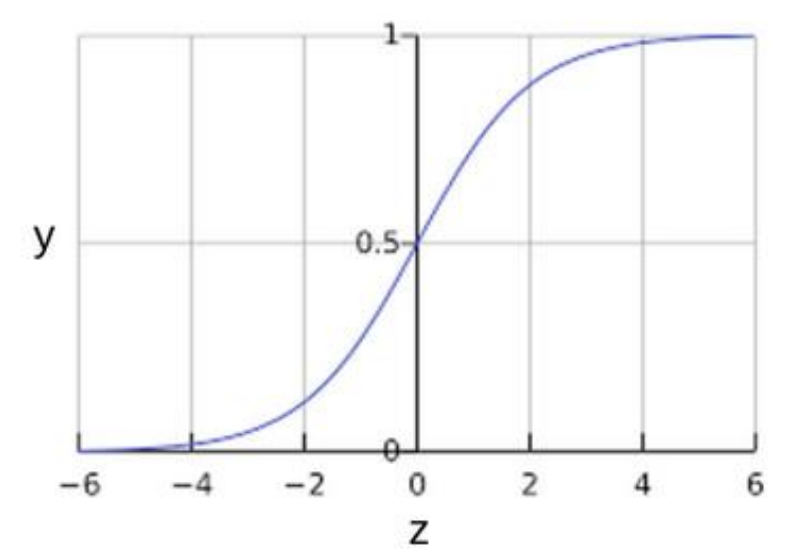
定义域为全体实数,值域在[0,1]之间,\(z\)值在0点对应的结果为\(0.5\),且sigmoid函数连续可微分。他的图像如下
损失函数
前面线性回归的损失函数是平方损失,如果逻辑回归的损失函数也定义为平方损失,那么:
这其中:𝑖表示第𝑖个样本点,\(𝑧_𝑖\) = \(𝑥_𝑖\) ∗ 𝑤 + 𝑏 ,𝜑\((𝑧_𝑖)\) 表示对𝑖个样本的预测值,\(𝑦_𝑖\)表示第𝑖个样本的标签值
那么将Sigmoid函数带入上述函数就会得到下面这张图像
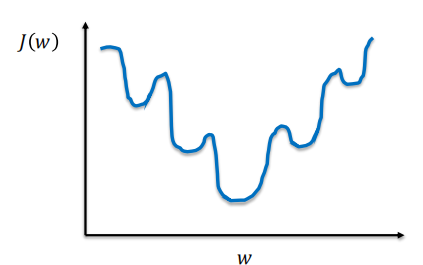
有个很明显的问题,这个函数是非凸函数,有多个极小值,如果采用梯度下降法,会容易导致陷入局部最优解中
在二元逻辑回归的损失函数一般采用对数损失函数,定义如下:
其中:(𝑥, 𝑦) ∈ 𝐷是有标签样本 (𝑥, 𝑦) 的数据集,𝑦是有标签样本中的标签,取值必须是 0 或 1,𝑦′是对于特征集𝑥的预测值(介于 0 和 1 之间)
它的图像就长下面这样
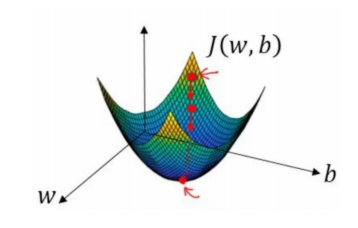
它就很明显是个凸函数了
多元分类
多元分类的基本模型如下
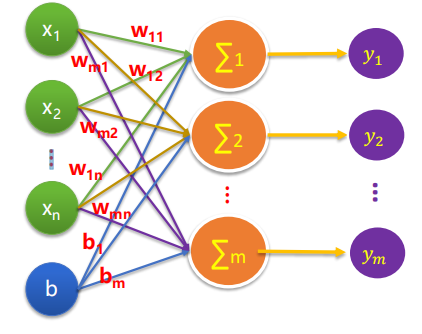
而我们要在这个基本模型上给他加一个softmax层
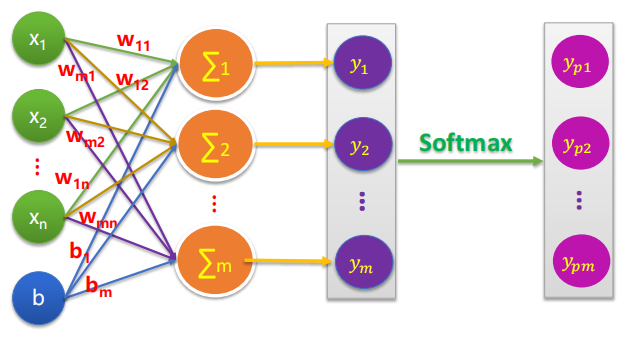
就长这个样子,这里有一个Softmax思想
逻辑回归可生成介于 0 和 1.0 之间的小数。例如,某电子邮件分类器的逻辑回归输出值为 0.8,表明电子邮件是垃圾邮件的概率为80%,不是垃圾邮件的概率为 20%。很明显,一封电子邮件是垃圾邮件或非垃圾邮件的概率之和为 1.0。
Softmax 将这一想法延伸到多类别领域。在多类别问题中,Softmax 会为每个类别分配一个用小数表示的概率。这些用小数表示的概率相加之和必须是 1.0。
可以举个例子
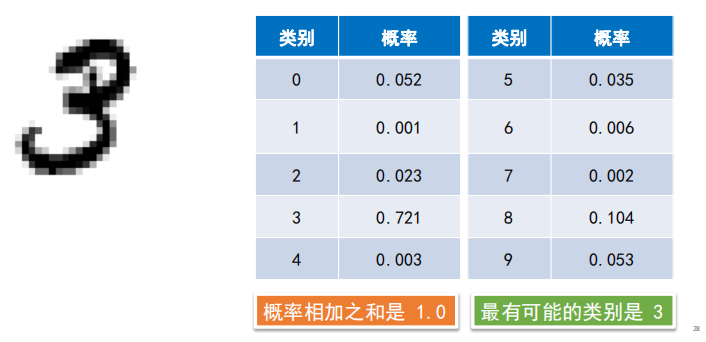
通俗的说就是那个概率大就选哪个,就和买彩票一样,实质上就是猜。
这里我们使用到的Softmax 方程式如下
这个公式本质上是将逻辑回归公式延伸到了多类别。
多分类问题中的标签数据与独热编码
在机器学习中特征之间距离的计算或相似度的常用计算方法都是基于欧式空间的,那么有时候就会产生一些问题,比如举个例子,对于下面这种编码方式,能说 1 比 8 更相似于 3 吗?

很显然,不可以!那怎么办呢,我们可以使用独热编码
独热编码 (one hot encoding)
一种稀疏向量,其中:
- 一个元素设为 1
- 所有其他元素均设为 0
独热编码常用于表示拥有有限个可能值的字符串或标识符。
那么为什么要用独热编码?
- 将离散特征的取值扩展到了欧式空间,离散特征的某个取值就对应欧式空间的某个点
- 机器学习算法中,特征之间距离的计算或相似度的常用计算方法都是基于欧式空间的
- 将离散型特征使用one-hot编码,会让特征之间的距离计算更加合理
同样上面这个例子,如果我们使用独热编码
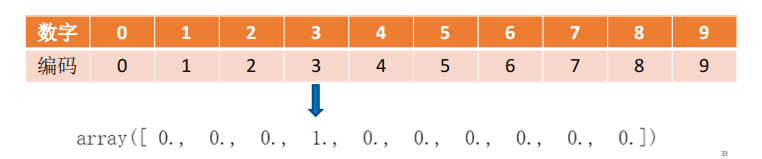
是不是很明显就合理了许多!
独热编码的一些操作
创建独热编码
import tensorflow as tf
x=[3,4]
tf.one_hot(x,depth=10)

这样我们就得到了3和4的独热编码
独热编码取值
独热编码的取值其实很简单,你只要找到值为1的那个下标就可以了,也就是找到最大值的下标,argmax()方法就可以完成这个操作,同样举几个例子
一维数组
>>>A=tf.constant([1,2,3])
>>>tf.argmax(A).numpy()
2
二维数组
二维数组我们可以通过axis参数来指定行列,axis=0为行,axis=1为列
B=tf.constant([[1,2,3],[4,5,6],[7,8,9]])
tf.math.argmax(B,axis=0).numpy()
Out[5]: array([2, 2, 2], dtype=int64)
tf.math.argmax(B,axis=1).numpy()
Out[6]: array([2, 2, 2], dtype=int64)
此外,万能的Numpy库也同样提供了这个方法
import numpy as np
C=np.array([[1,2,3],[4,5,6],[7,8,9]])
np.argmax(C,axis=1)
Out[10]: array([2, 2, 2], dtype=int64)
np.argmax(C,axis=0)
Out[11]: array([2, 2, 2], dtype=int64)
交叉熵损失
在这个实验中,我们所使用的是交叉熵(shang)损失
交叉熵是一个信息论中的概念,它原来是用来估算平均编码长度的。给定两个概率分布p和q,通过q来表示p的交叉熵为
交叉熵刻画的是两个概率分布之间的距离,p代表正确答案,q代表的是预测值,交叉熵越小,两个概率的分布约接近
举个例子
假设有一个3分类问题,某个样例的正确答案是(1,0,0)
甲模型经过softmax回归之后的预测答案是(0.5,0.2,0.3)
乙模型经过softmax回归之后的预测答案是(0.7,0.1,0.2)
那么
𝑯 ((1, 𝟎, 𝟎) , (𝟎. 𝟓, 𝟎. 𝟐, 𝟎. 𝟑)) = -log𝟎.𝟓 ≈ 0.301
𝑯 ((1, 𝟎, 𝟎) , (𝟎. 𝟕, 𝟎. 𝟏, 𝟎. 𝟐))= -log𝟎.𝟕 ≈ 0.155
交叉熵损失函数定义为:
理论篇到此为止,实战篇请看:
MNIST手写数字识别:分类应用入门(实践篇)
学习笔记,仅供参考,如有错误,敬请指正!

