单变量线性回归:TensorFlow 实战(实战篇)
导语
慕课:《深度学习应用开发-TensorFlow实践》
章节:第五讲 单变量线性回归:TensorFlow 实战
这一讲理论部分请看https://www.cnblogs.com/tangkc/p/15371331.html,TensorFlow版本为2.3
我们所要实现的是一个单变量的线性方程,这个方程可以表示为y=w*x+b。本案例通过生成人工数据集,随机生成一个近似采样随机分布,使得w=2.0,b=1,并加入一个噪声,噪声的最大振幅为0.4
导入库并生成数据集
导入库
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
#在jupyter中使用matplotlib显示图像需要设置为inline模式,否则不会在网页中显示图像
%matplotlib inline
tf.__version__
output:
2.3.0
生成数据集
首先生成输入数据,构造满足这个函数的x和y,同时加入一些不满足方程的噪声
#直接采用np生成等差数列的方法,生成100个点,取值在[-1,1]
x_data=np.linspace(-1,1,100)
np.random.seed(5)#设置随机数种子
#产生对应的y=2x+1的值,同时加入噪声
y_data=2*x_data+1.0+np.random.randn(*x_data.shape)*0.4
np.random.randn是从标准正态分布中返回一个或多个样本值,举个简单的例子
而源代码中的np.random.randn(*x_data.shape)效果和np.random.randn(100)是一样的
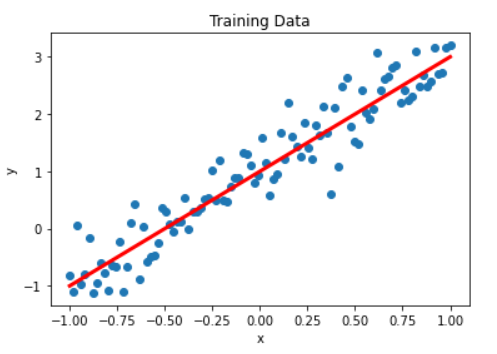
下面我们画一下生成的x和y的图像
plt.scatter(x_data,y_data)
plt.xlabel('x')
plt.ylabel('y')
plt.title("Training Data")
# 画出我们想要得到的目标函数y=2x+1
plt.plot(x_data,1.0+2*x_data,'r',linewidth=3)
构建模型
建模
这个模型还是比较的简单的
def model(x,w,b):
return tf.multiply(x,w)+b
创建待优化变量
w=tf.Variable(np.random.randn(),tf.float32)# 斜率
b=tf.Variable(0.0,tf.float32)#截距
定义损失函数
损失函数用于描述预测值和真实值之间的误差,从而指导模型收敛方向,常用的有均方差(MSE)和交叉熵
这里我们用的是均方差
#定义均方差损失函数
def loss(x,y,w,b):
err=model(x,w,b)-y#计算预测值和真实值之间的差异
squarred_err=tf.square(err)#求平方,得出方差
return tf.reduce_mean(squarred_err)#求均值,得出均方差
训练模型
设置训练超参数
epochs=10#迭代次数
lr=0.01#学习率
定义计算梯度函数
def grad(x,y,w,b):
with tf.GradientTape() as tape:
loss_=loss(x,y,w,b)
return tape.gradient(loss_,[w,b])# 返回梯度向量
这里有一个TF1和TF2不同的地方,在 TensorFlow 2 中,使用 tf.GradientTape() 这一上下文管理器封装需要求导的计算步骤,并使用其 gradient() 方法求导。
执行训练(SGD)
step=0# 记录训练步数
loss_list=[]# 保存loss值的列表
display_step=10# 控制训练过程数据数据显示频率,不是超参数
for epoch in range(epochs):
for xs,ys in zip(x_data,y_data):
loss_=loss(xs,ys,w,b)# 计算loss
loss_list.append(loss_)
delta_w,delta_b=grad(xs,ys,w,b)#计算梯度
change_w=delta_w*lr#计算w需要调整的量
change_b=delta_b*lr#计算b需要调整的量
w.assign_sub(change_w)
b.assign_sub(change_b)#将w,b变更为减去对应变化量后的值
step=step+1
if step%display_step==0:#显示训练过程
print(f'Training Epoch:{epoch+1} Step:{step} Loss:{loss_}')
plt.plot(x_data,w.numpy()*x_data+b.numpy())
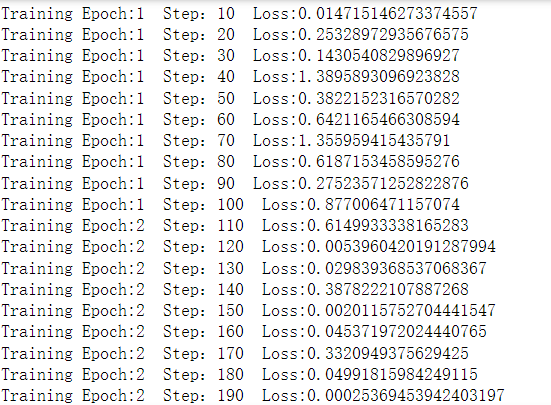
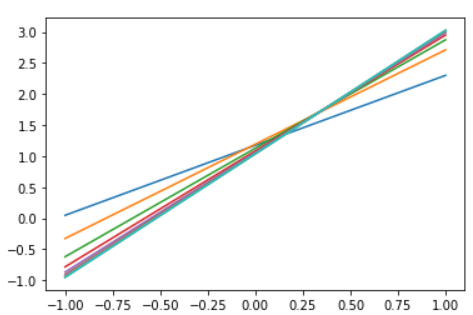
这里就展示一部分的运行结果
本案例所拟合的模型较简单,训练5轮之后已经接近收敛,对于复杂模型,需要更多次训练才能收敛
显示训练结果并可视化
print(f'w:{w.numpy()}, b:{b.numpy()}')

plt.scatter(x_data,y_data,label='Original data')
plt.plot(x_data,x_data*2.0+1.0,label="Object line",color='g',linewidth=3)
plt.plot(x_data,x_data*w.numpy()+b.numpy(),label="Fitted line",color='r',linewidth=3)
plt.legend(loc=2)#设置图例位置
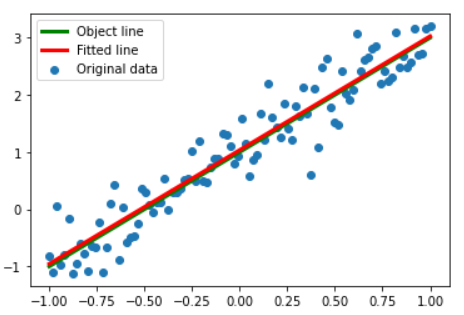
查看损失变化情况
plt.plot(loss_list)
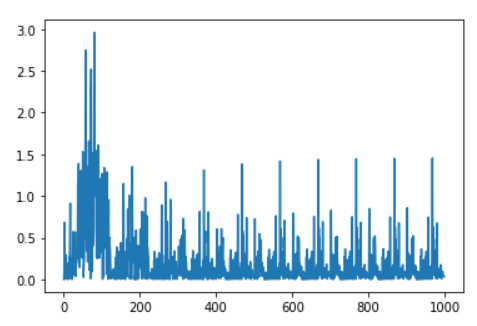
进行预测
x_test=3.21
predict=model(x_test,w.numpy(),b.numpy())
target=2*x_test+1.0
print(f'预测值:{predict}, 目标值:{target}')
输出
预测值:7.426405906677246, 目标值:7.42
批量梯度下降BGD模型训练
随机梯度下降法 (SGD) 每次迭代只使用一个样本(批量大小为 1),如果进行足够的迭代,SGD 也可以发挥作用。“随机”这一术语表示构成各个批量的一个样本都是随机选择的。
在梯度下降法中,批量指的是用于在单次迭代中计算梯度的样本总数。
假定批量是指整个数据集,数据集通常包含很大样本(数万甚至数千亿),此外,数据集通常包含多个特征。因此,一个批量可能相当巨大。如果是超大批量,则单次迭代就可能要花费很长时间进行计算。
小批量随机梯度下降法(小批量 SGD) 是介于全批量迭代与 SGD 之间的折衷方案。小批量通常包含 10-1000 个随机选择的样本。小批量 SGD 可以减少 SGD 中的杂乱样本数量,但仍然比全批量更高效。
那么,接下来是实现,我们只需要修改一下上面的一部分代码就好了。
修改训练超参数
epochs=100#迭代次数
lr=0.05#学习率
训练周期和学习率需要做一些调整。训练周期暂设为100,意味着所有样本要参与100次训练。学习率设置为0.05,比SGD版本的要大。
修改模型训练过程
loss_list=[]# 保存loss值的列表
for epoch in range(epochs):
loss_=loss(x_data,y_data,w,b)# 计算loss
loss_list.append(loss_)
delta_w,delta_b=grad(x_data,y_data,w,b)#计算梯度
change_w=delta_w*lr#计算w需要调整的量
change_b=delta_b*lr#计算b需要调整的量
w.assign_sub(change_w)
b.assign_sub(change_b)#将w,b变更为减去对应变化量后的值
print(f'Training Epoch:{epoch+1} Loss={loss_}')
plt.plot(x_data,w.numpy()*x_data+b.numpy())
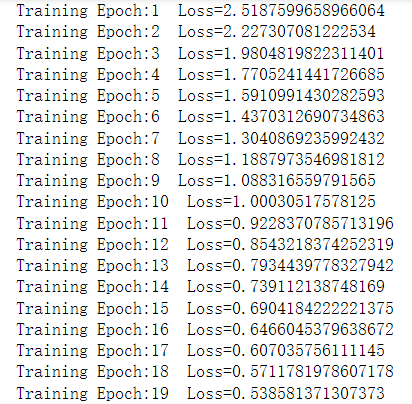
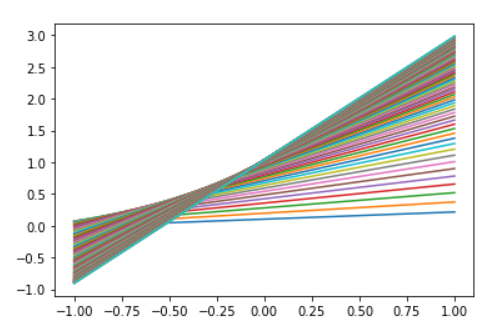
显示训练结果并可视化
print(f'w:{w.numpy()}, b:{b.numpy()}')
plt.scatter(x_data,y_data,label='Original data')
plt.plot(x_data,x_data*2.0+1.0,label="Object line",color='g',linewidth=3)
plt.plot(x_data,x_data*w.numpy()+b.numpy(),label="Fitted line",color='r',linewidth=3)
plt.legend(loc=2)#设置图例位置
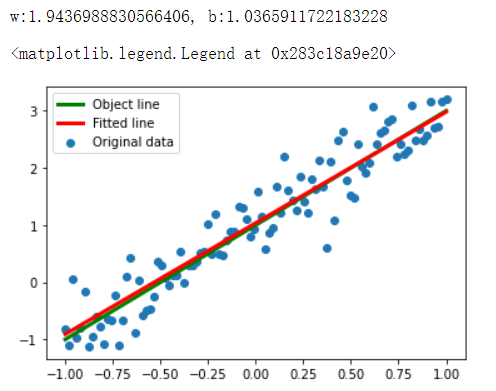
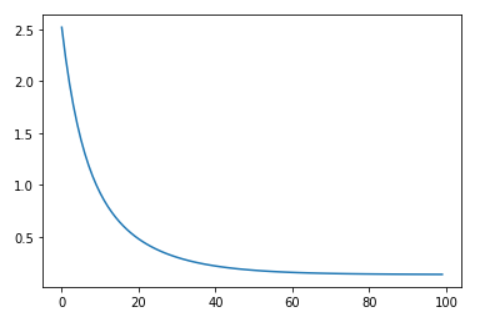
损失值可视化
plt.plot(loss_list)
完整代码
点击查看代码
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
#在jupyter中使用matplotlib显示图像需要设置为inline模式,否则不会在网页中显示图像
%matplotlib inline
#直接采用np生成等差数列的方法,生成100个点,取值在[-1,1]
x_data=np.linspace(-1,1,100)
np.random.seed(5)#设置随机数种子
#产生对应的y=2x+1的值,同时加入噪声
y_data=2*x_data+1.0+np.random.randn(*x_data.shape)*0.4
# np.random.randn是从标准正态分布中返回一个或多个样本值,
np.random.randn(10)
plt.scatter(x_data,y_data)
plt.xlabel('x')
plt.ylabel('y')
plt.title("Training Data")
# 画出我们想要得到的目标函数y=2x+1
plt.plot(x_data,1.0+2*x_data,'r',linewidth=3)
def model(x,w,b):
return tf.multiply(x,w)+b
w=tf.Variable(np.random.randn(),tf.float32)# 斜率
b=tf.Variable(0.0,tf.float32)#截距
#定义均方差损失函数
def loss(x,y,w,b):
err=model(x,w,b)-y#计算预测值和真实值之间的差异
squarred_err=tf.square(err)#求平方,得出方差
return tf.reduce_mean(squarred_err)#求均值,得出均方差
def grad(x,y,w,b):
with tf.GradientTape() as tape:
loss_=loss(x,y,w,b)
return tape.gradient(loss_,[w,b])# 返回梯度向量
epochs=100#迭代次数
lr=0.05#学习率
loss_list=[]# 保存loss值的列表
for epoch in range(epochs):
loss_=loss(x_data,y_data,w,b)# 计算loss
loss_list.append(loss_)
delta_w,delta_b=grad(x_data,y_data,w,b)#计算梯度
change_w=delta_w*lr#计算w需要调整的量
change_b=delta_b*lr#计算b需要调整的量
w.assign_sub(change_w)
b.assign_sub(change_b)#将w,b变更为减去对应变化量后的值
print(f'Training Epoch:{epoch+1} Loss={loss_}')
plt.plot(x_data,w.numpy()*x_data+b.numpy())
print(f'w:{w.numpy()}, b:{b.numpy()}')
plt.scatter(x_data,y_data,label='Original data')
plt.plot(x_data,x_data*2.0+1.0,label="Object line",color='g',linewidth=3)
plt.plot(x_data,x_data*w.numpy()+b.numpy(),label="Fitted line",color='r',linewidth=3)
plt.legend(loc=2)#设置图例位置
plt.plot(loss_list)
梯度下降算法总结
批量梯度下降每次迭代都考虑了全部的样本,做的是全局优化,但花费的计算资源较大,如果训练数据非常大,还无法实现全部样本同步参与。
随机梯度下降每次迭代只取一条样本数据, 由于单个样本的训练可能会带来很多噪声,使得SGD并不是每次迭代都向着整体最优化方向,因此在刚开始训练时可能收敛得很快,但是训练一段时间后就会变得很慢。
在SGD和BGD中间,还有一个集合了两种梯度下降法的优点的方法:小批量梯度下降(MBGD,Mini-batch gradient descent),每次迭代从训练样本中随机抽取一小批进行训练,这个一小批的数量取值也是一个超参数。
小结
通过一个简单的例子介绍了利用Tensorflow实现机器学习的思路,重点讲解了下述步骤:
- 生成人工数据集及其可视化
- 构建线性模型
- 定义损失函数
- (梯度下降) 优化过程
- 训练结果的可视化
- 利用学习到的模型进行预测
学习笔记,仅供参考,如有错误,敬请指正!
同时发布在CSDN中:https://blog.csdn.net/tangkcc/article/details/120624865



 浙公网安备 33010602011771号
浙公网安备 33010602011771号