LeetCode|1411. 给 N x 3 网格图涂色的方案数
你有一个 n x 3 的网格图 grid ,你需要用 红,黄,绿 三种颜色之一给每一个格子上色,且确保相邻格子颜色不同(也就是有相同水平边或者垂直边的格子颜色不同)。
给你网格图的行数 n 。
请你返回给 grid 涂色的方案数。由于答案可能会非常大,请你返回答案对 10^9 + 7 取余的结果。
示例 1:
输入:n = 1
输出:12
解释:总共有 12 种可行的方法: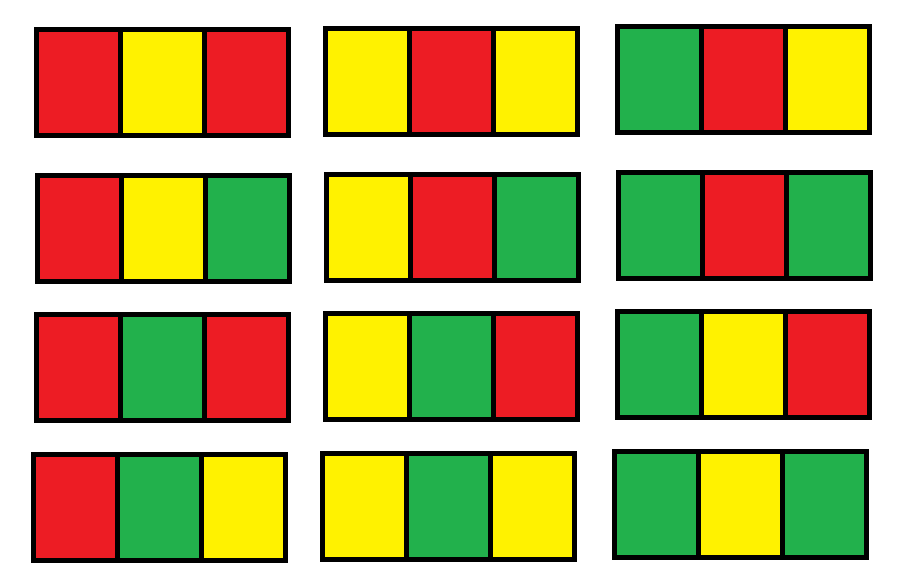
示例 2:
输入:n = 2
输出:54
示例 3:
输入:n = 3
输出:246
示例 4:
输入:n = 7
输出:106494
示例 5:
输入:n = 5000
输出:30228214
提示:
-
n == grid.length
-
grid[i].length == 3
-
1 <= n <= 5000
解题思路
题目分析
这里本来是要用动态规划的,而且比较麻烦,但是其实这题是可以找规律的,用数学方法解决会比较简单
观察LeetCode给的N=1示例,可以抽象区分为2种类型,ABA和ABC,也即涂两种颜色和三种颜色都涂。
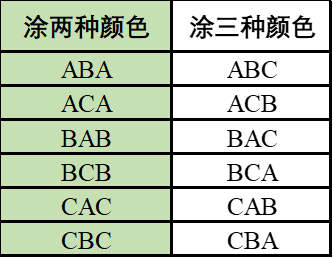
分情况讨论,可知,在下方增加1行时,有9种情况,又可以分为ABA和ABC两个大类

本层的结果 \(=A B A\) 类的个数 \(m+A B C\) 类的个数 \(n\)
本层的每个 \(ABA\) 类 \(=>\) 下层演化 3 个 \(A B A+2\) 个 \(A B C\)
本层的每个 \(A B C\) 类 \(=>\) 下层演化 2 个 \(A B A+2\) 个 \(A B C\)
下层的结果 \(=A B A\) 类的个数 \(+A B C\) 类的个数 \(=(3 m+2 n)+(2 m+2 n)\)
Python代码实现
class Solution:
def numOfWays(self, n: int) -> int:
mod = 10**9 +7
if n == 1:
return 12
repeat = 6
unrepeat = 6
for i in range(n-1):
new_repeat = repeat * 3 + unrepeat *2
new_unrepeat = repeat * 2 + unrepeat *2
repeat = new_repeat
unrepeat = new_unrepeat
return (repeat + unrepeat) % mod

