基于无人机平台的三维校园建模

研究区域模型建立

数据导入与配置

打开Pix4Dmapper软件，选择“新项目”，并配置项目对应名称与路径。

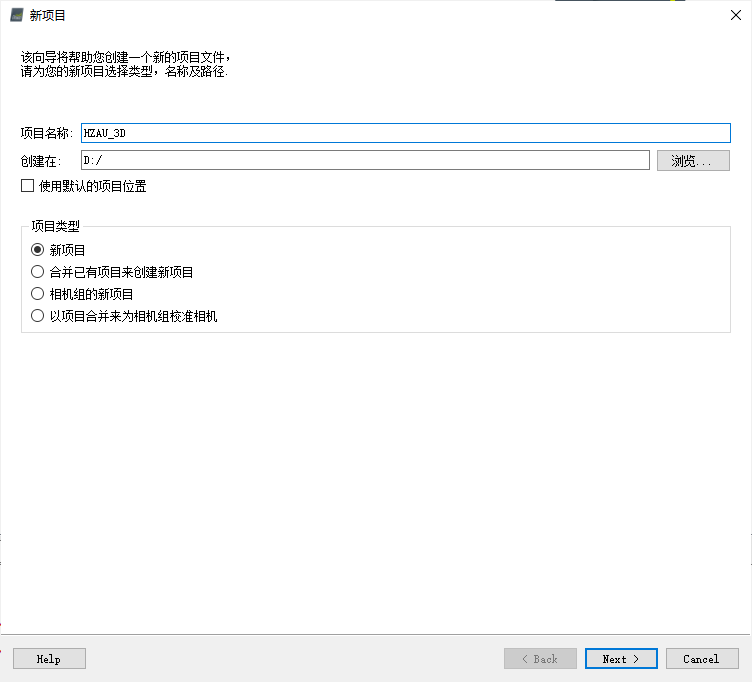
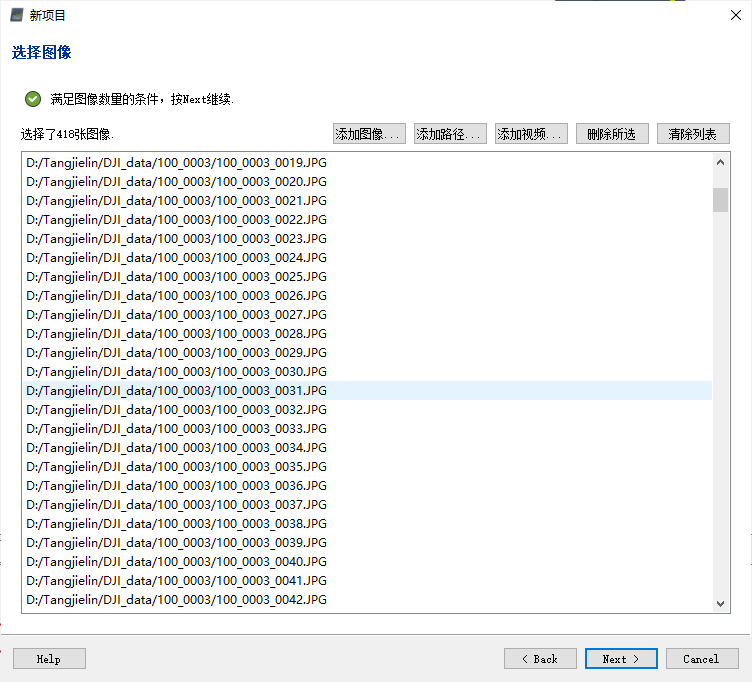
随后，将前述下载好的图像文件导入项目中。其中，可以将全部整理好的图像放置于同一文件夹下，并通过“添加路径…”的方式将多张图像批量导入新项目中，“选择图像”过程如下图所示。

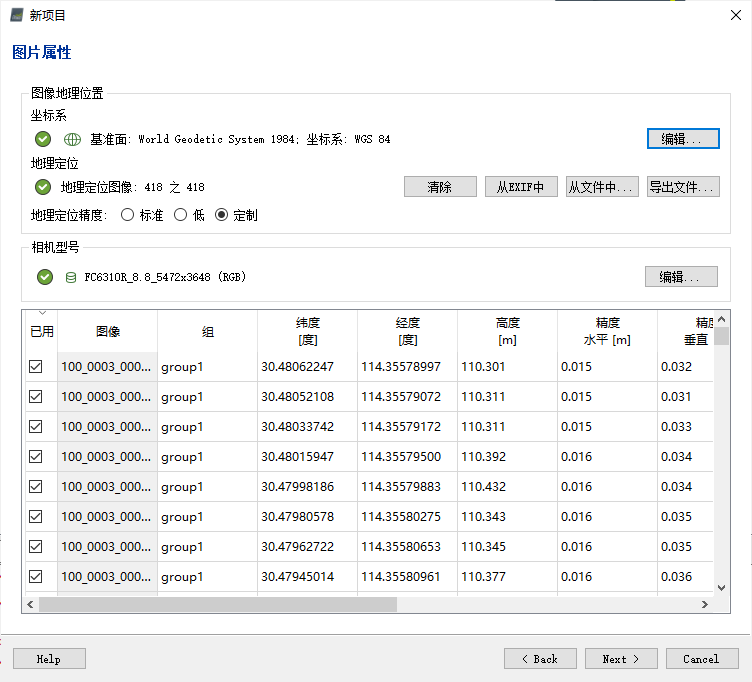
随后，对图像坐标系、相机属性等参数加以配置，其中程序亦会给出默认参数；这些参数需要根据图像拍摄时无人机摄像机所处的状态、所选用的坐标系决定。同时还可浏览各图像对应经纬度、高度、位置精度、方向角度等信息，如下图所示。

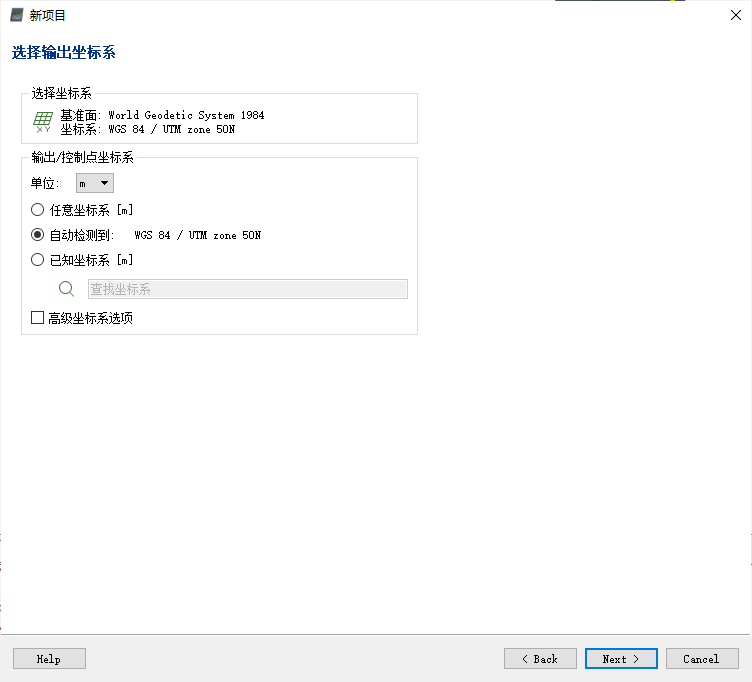
随后，对输出结果与地面控制点（Ground Control Point，GCP）坐标系加以配置。默认条件下，二者对应坐标系一致，以此使得建模结果与GCP同处于同一坐标系中；如二者不一致，而若其对应坐标系分别均存在于软件坐标系数据库中，软件亦将自动实现两种坐标系的转换。
此外，还可对坐标系单位（默认为米）等加以调整。其中，若图像自身含有空间位置信息，则可选择自动检测。

随后，对处理选项模板加以配置。在左侧选择“标准”→“3D Maps”，软件将自动以“3D地图”模板进行应用处理。

打开“处理选项”，需要选中三个选项，并配置相关属性，如下图所示。

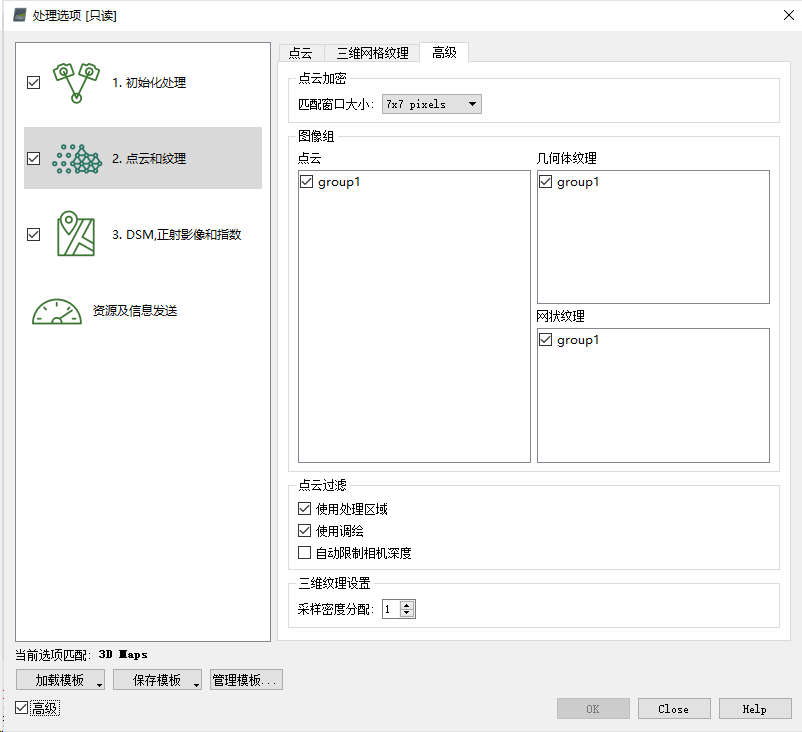
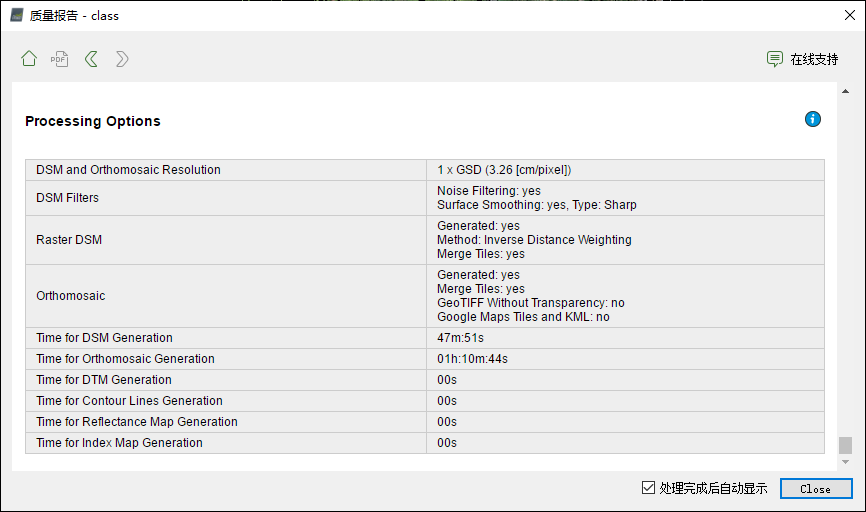
可以看到，在程序运行一段时间后（约20分钟左右），即可自动弹出质量报告界面。如下图所示。由此可知，此时程序已完成部分工作：

在质量报告中可以查看初始化处理后的和DSM如下：

所得到研究区域的初步模型如下图所示：

尽管已弹出质量报告，但程序依然在运行，且报告中内容会逐步添加。

模型外观检查与调整

运行完成后，得到最终版质量报告，如下图所示：

得到空间三维模型如下图所示：

随后，对所得研究区域空间三维模型加以细致浏览，发现所得模型除部分地物侧面形状具有偏差、部分建筑物纹理出现混乱外，并无其它明显问题；模型在整体地势、建筑物位置与大致形状等方面均整体较为良好。

其中，可能会出现一些与模型其他位置相独立等错误的点云，我们可以将其删除。选择“Edit Densified Point Cloud”选项，用鼠标左键将其圈画，如下图所示。

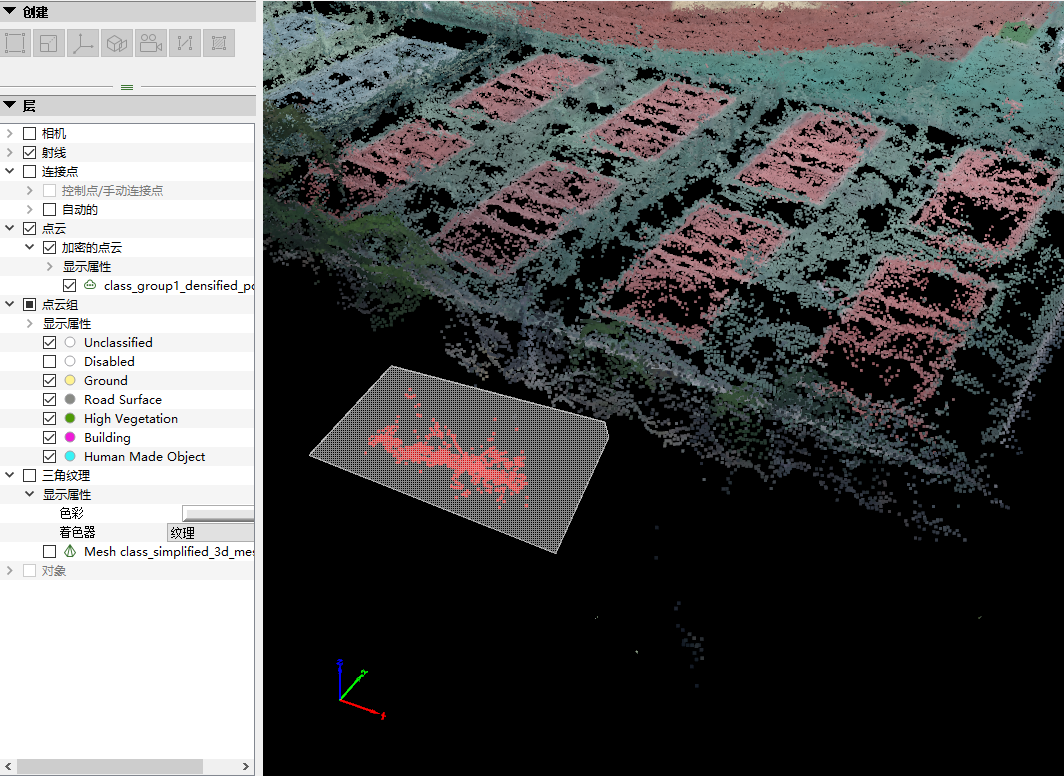
完毕后，点击鼠标右键，即可实现对圈画区域内点的选取。所选中的点呈现红色，如下图所示。

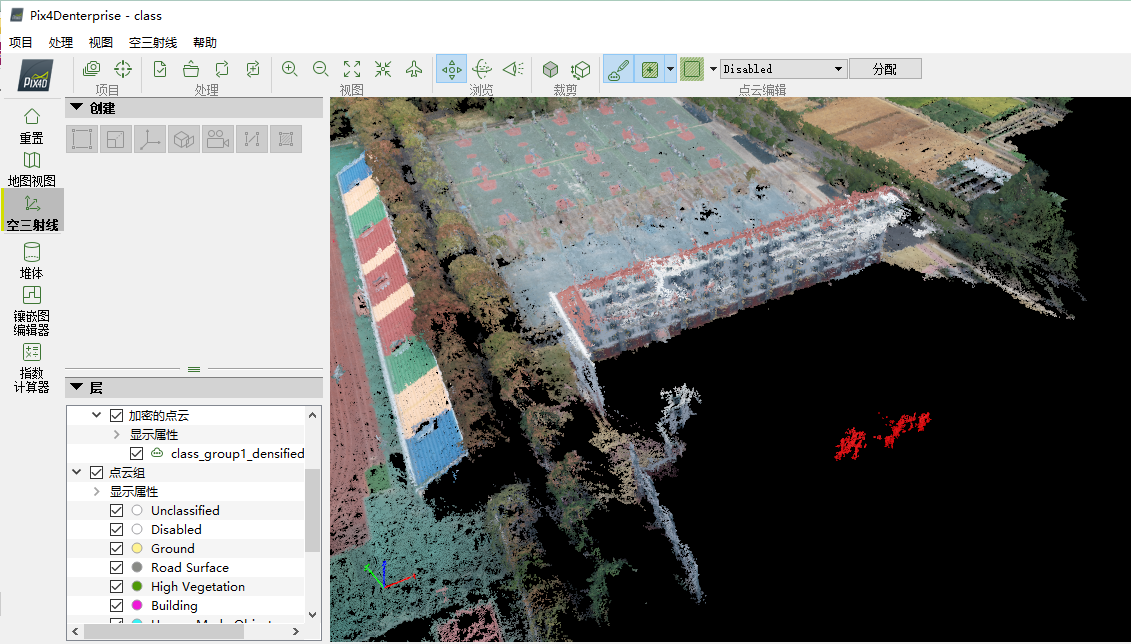
随后，将其归类为“Disabled”，点击“分配”，所选择的点即可消除，如下图所示

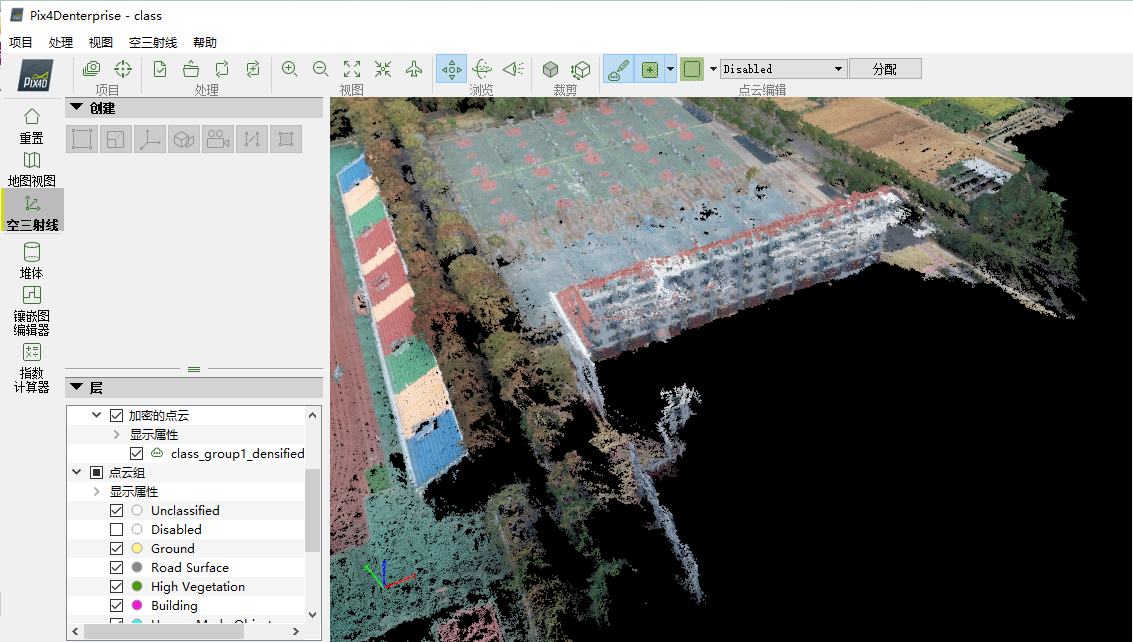
通过上述步骤，即可将所得空间三维模型中效果较差的点或点云加以选择与去除。完成后，退出编辑状态，重新生成纹理，如下图所示。

模型量测分析

得到模型后，可以对模型中具有代表性的地物加以量测。可量测的指标包括地物长度、面积、体积等；通过量测，可以对模型加以定量角度的检验，同时可由模型中获取更多信息。具体测量方法为利用“New Surface”功能将其基部包围，从而得到其底面周长（二维与三维）以及占地面积（二维与三维）。

肉类科学研究所的周长与占地面积量测

量测对象	地形三维长度(m)	投射二维长度(m)	封闭的三维面积(m2)	投射二维面积(m2)
肉类科学研究所	145.31	118.33	752.51	571.76

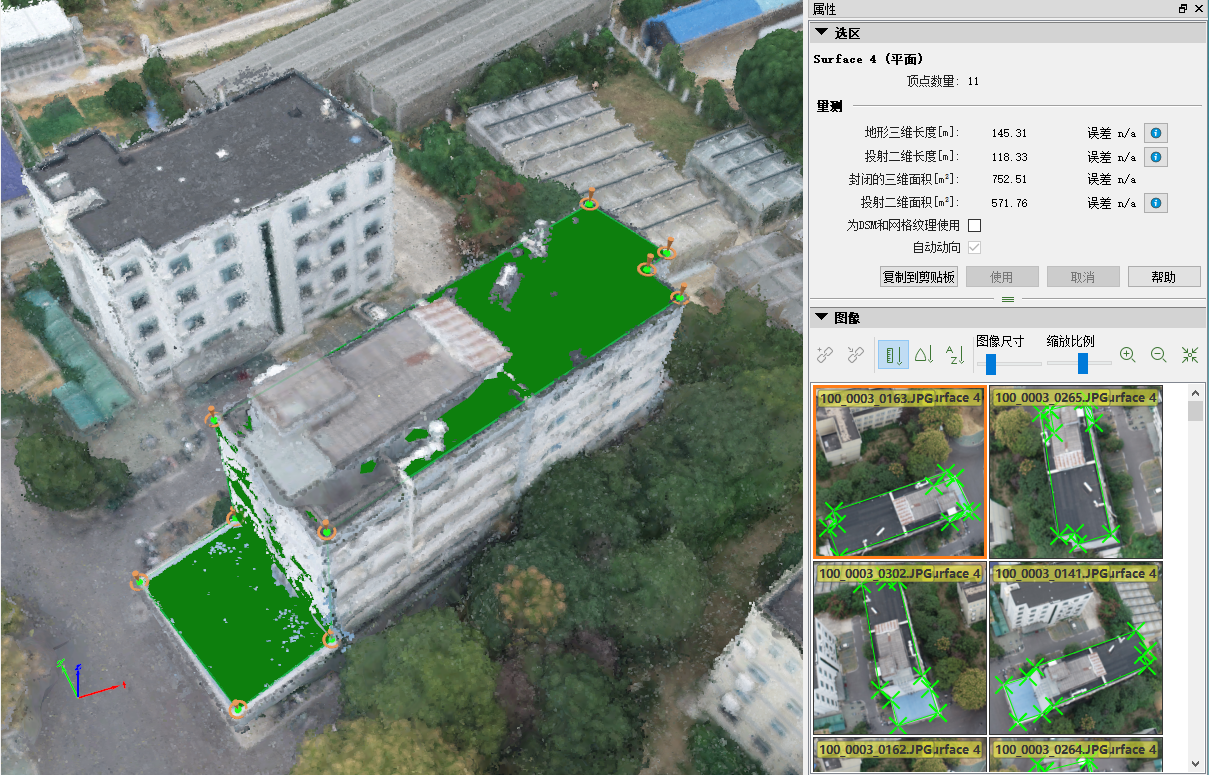
博园宿舍1栋的周长与占地面积量测

量测对象	地形三维长度(m)	投射二维长度(m)	封闭的三维面积(m2)	投射二维面积(m2)
博园宿舍1栋	169.12	156.03	515.17	485.52

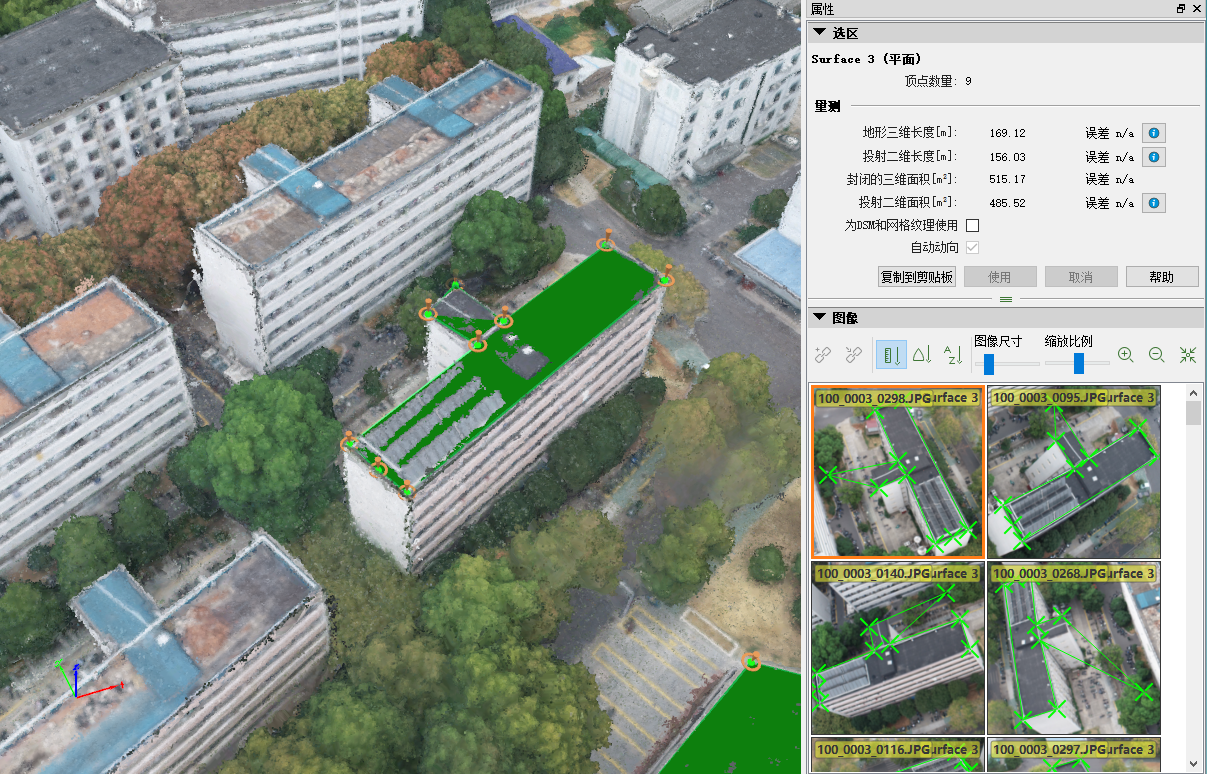
博园宿舍3栋的周长与占地面积量测

量测对象	地形三维长度(m)	投射二维长度(m)	封闭的三维面积(m2)	投射二维面积(m2)
博园宿舍3栋	286.13	281.65	1638.47	1538.63

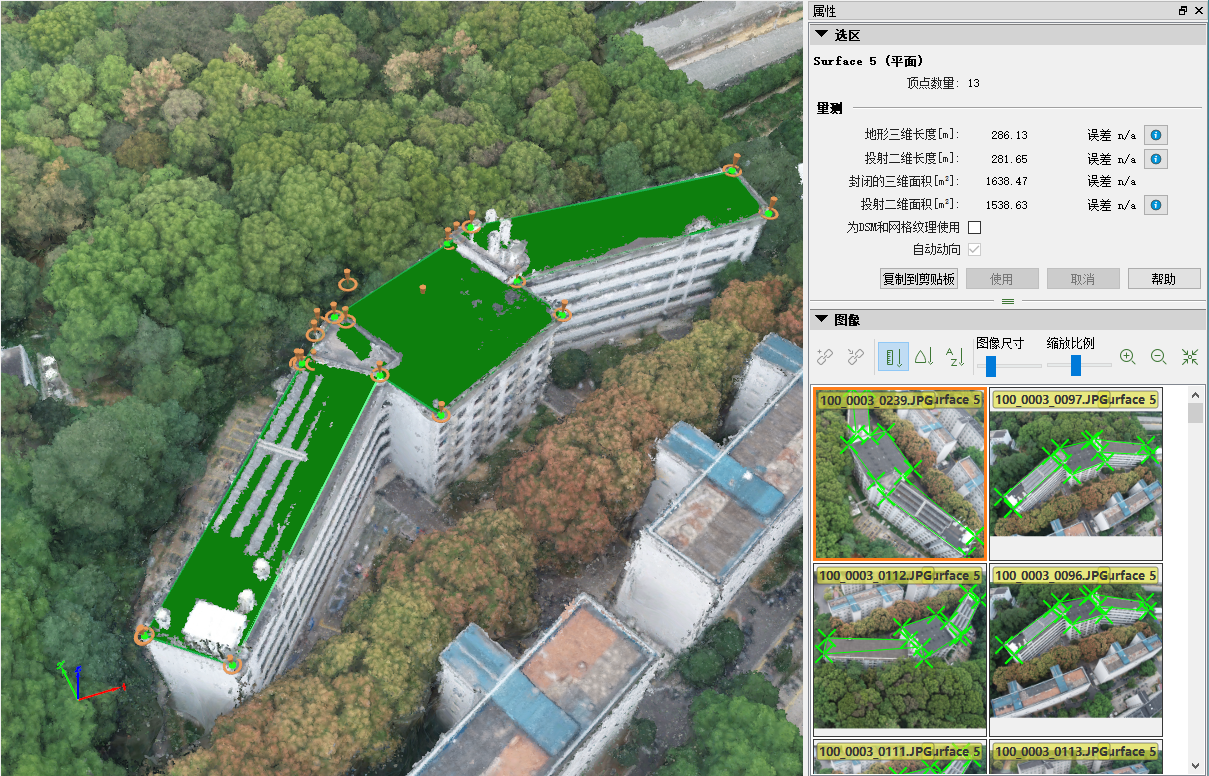
橘园食堂的周长与占地面积量测：

量测对象	地形三维长度(m)	投射二维长度(m)	封闭的三维面积(m2)	投射二维面积(m2)
橘园	157.43	156.04	1537.93	1518.14

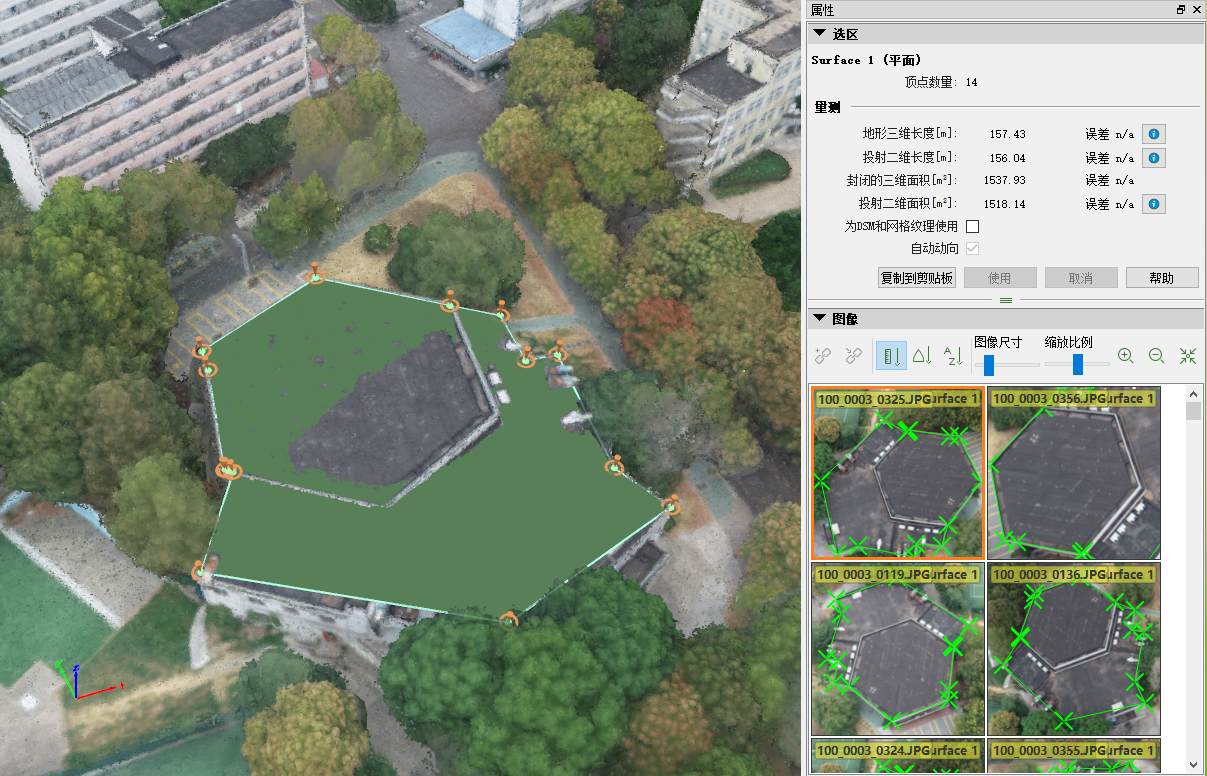
第二运动场足球场的周长与占地面积量测

量测对象	地形三维长度(m)	投射二维长度(m)	封闭的三维面积(m2)	投射二维面积(m2)
第二运动场足球场	350.46	350.42	7499.03	7497.84

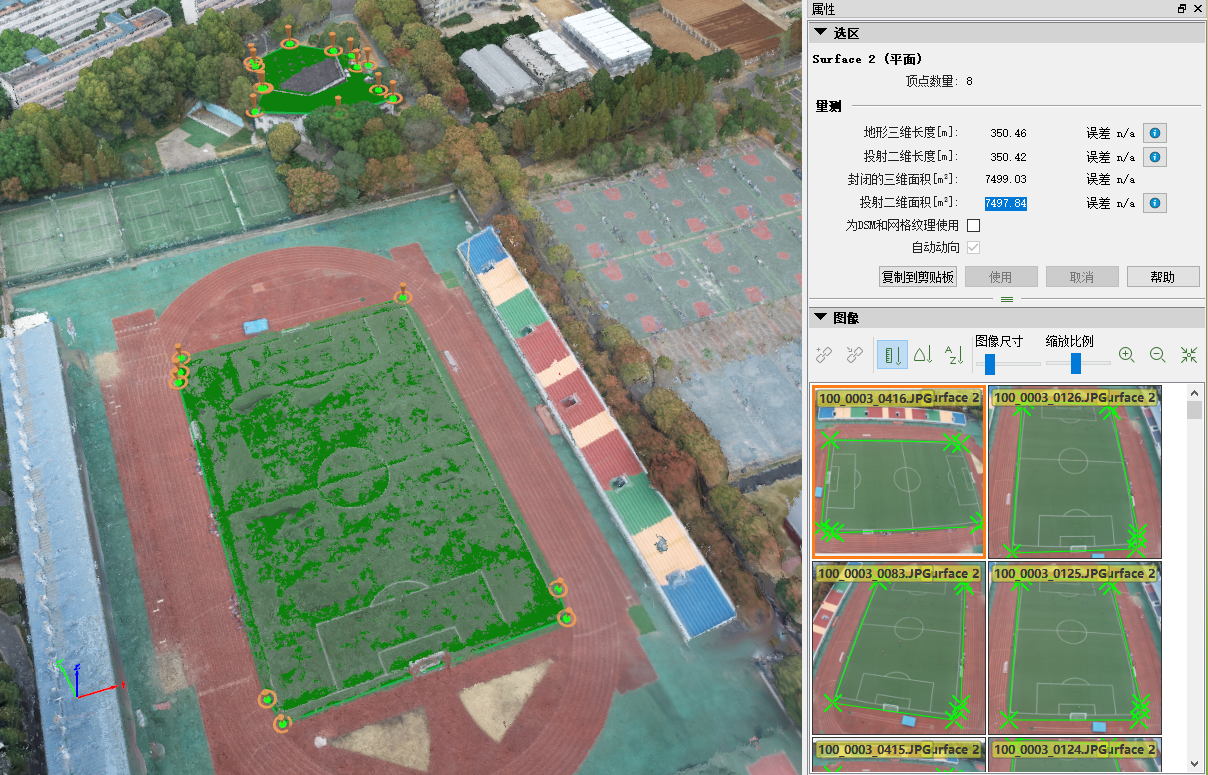
三维空间分析

坡度与坡向分析

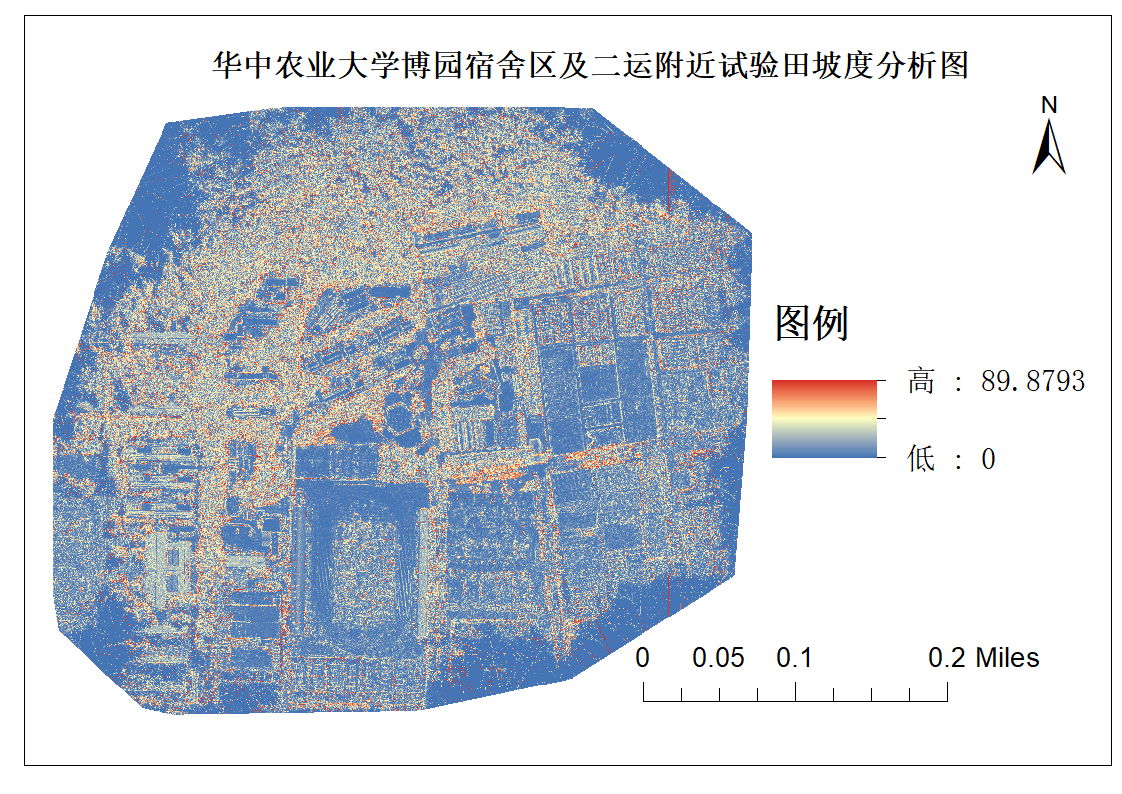
利用三维建模所得部分校园区域DSM数据，求取其坡度和坡向信息，如下图所示。

可以发现，狮子山上的博园宿舍区坡度较大，试验田处坡度较小，同时由于使用DSM建模，建筑轮廓被清晰的勾选出来。

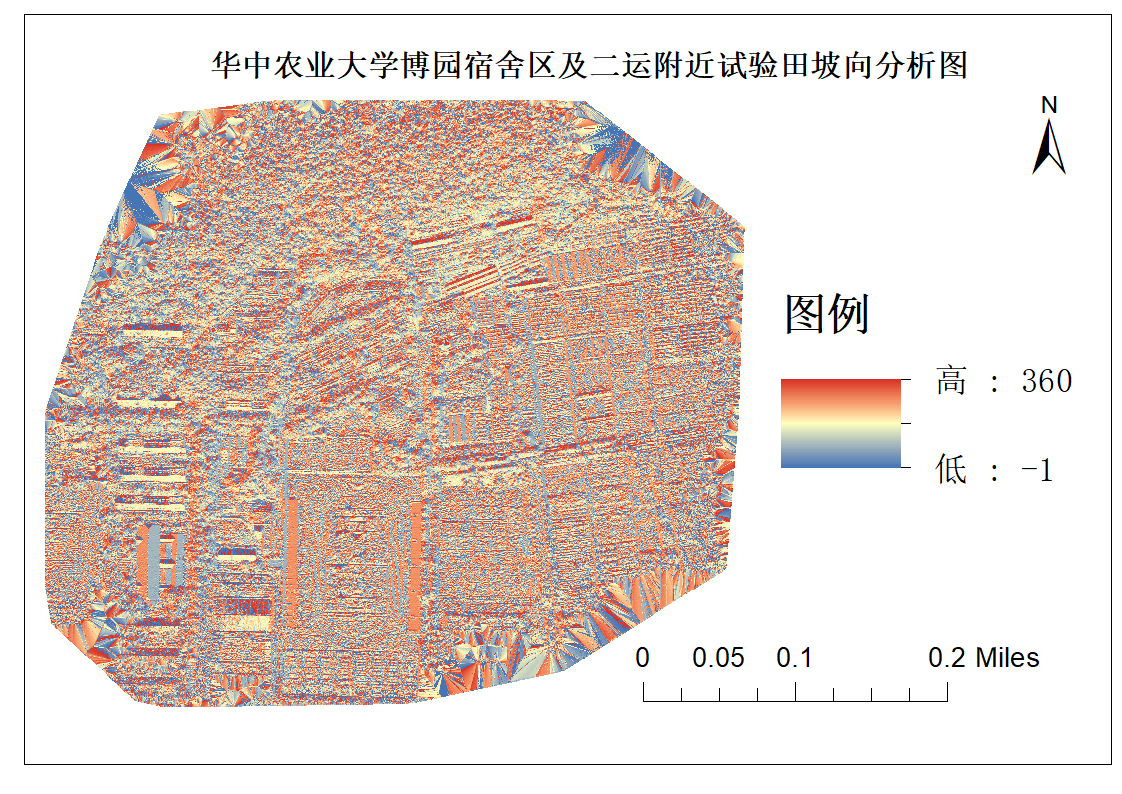
可以发现，大部分建筑的南北向的墙的坡向值在360附近，证明我们学校的建筑大致还是沿正南正北方向修建的，同样由于使用DSM建模，建筑轮廓被清晰的勾选出来，南北向的墙的坡向值在360附近，东西向的墙的坡向值在180附近。

水淹分析

考虑到该所学校所在城市整体地势，以及过去一段时间曾在该城市发生过的洪涝灾害实例。首先，选择以m水位为阈值，对区域整体防洪能力加以区分。其中，防洪能力较高区域即指8m水位无法淹没区域。所得结果如下图所示。

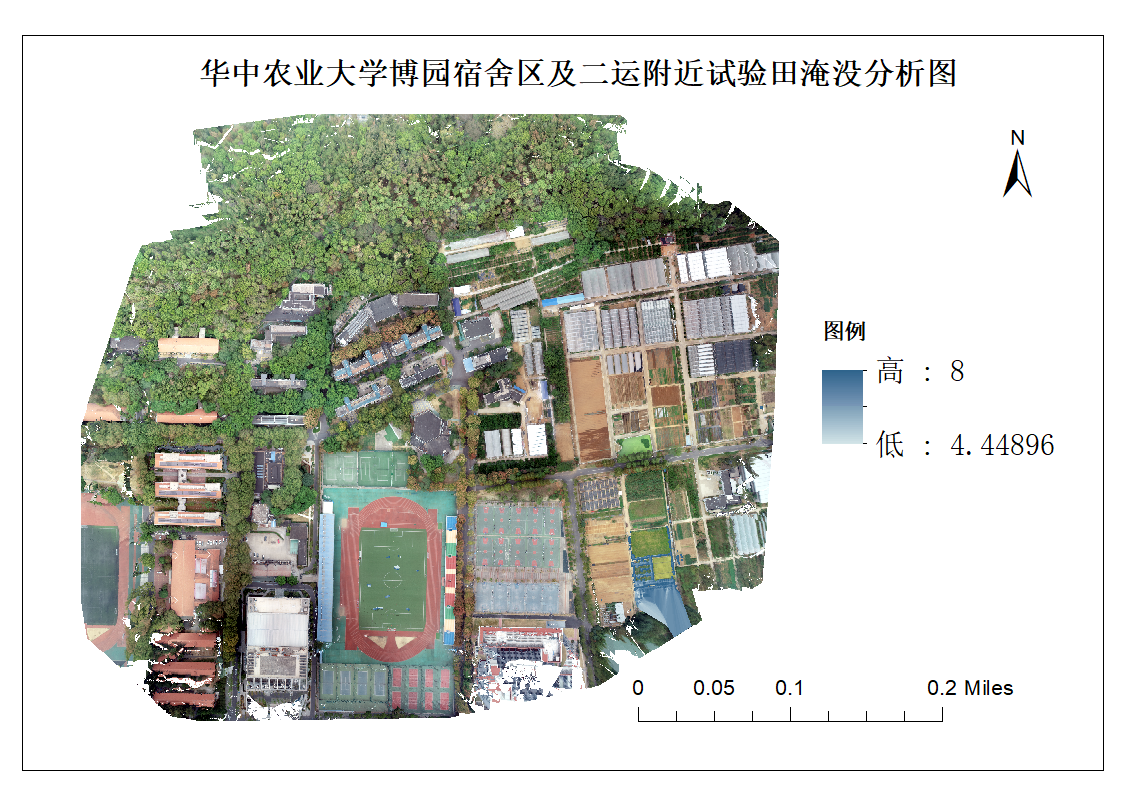
可以看到，仅仅在研究区域东南角具有部分淹没区域。由于这一区域面积较小，因此考虑适当加大淹没分析对应阈值。

以16m水位作为阈值，利用同样的方法对研究区域进行淹没分析，所得结果如下图所示。

可以看到，只有狮子山上的博园宿舍区未被淹没，可见住在地势较高处还是有一定好处的。

建模原理

运动结构恢复（Structure from Motion）介绍

在传统的摄影测量方法中，通常是利用 2 幅影像来构建立体模型，且为了解求地面点的三维空间坐标，通常要求相机的位置与姿态是已知的，或者需要大量物方空间坐标已知的地面控制点去解求相机的方位与姿态。而SFM 方法最早起源于计算机视觉领域，它是指通过运动着的相机获取的多视图像集，估计出相机的位姿( Motion) 并重建场景结构( Structure) 的过程 。

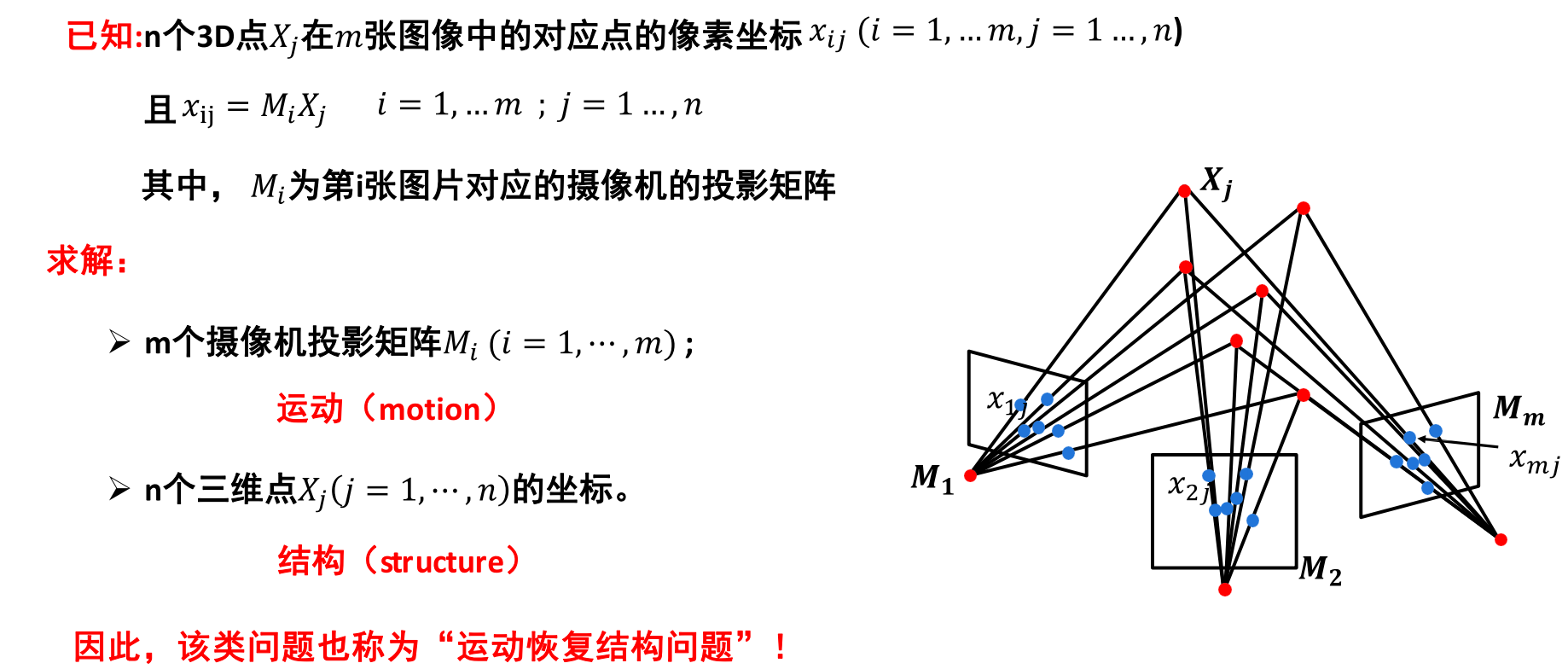
在应用方面，以城市三维建模为例，获取复杂现实场景或目标物的精确真实三维模型的方式可粗略分为接触与非接触方式。非接触方式之一是基于影像的三维建模技术，因为SFM技术的广泛应用以及低成本，采用SFM三维建模是计算机视觉领域的研究热点。大到对以无人机为主要搭载平台所获取的大区域序列影像，恢复城市三维结构，小到对某一个建筑物，如利用老城区中古建筑文物的序列影像进行精细建模，结合现在的深度学习技术对古建筑中的裂缝等目标进行检测并提取，再根据SFM获取的影像姿态信息进行三维投影，可以定量地分析受损情况，便于下一步制定保护措施。

算法原理

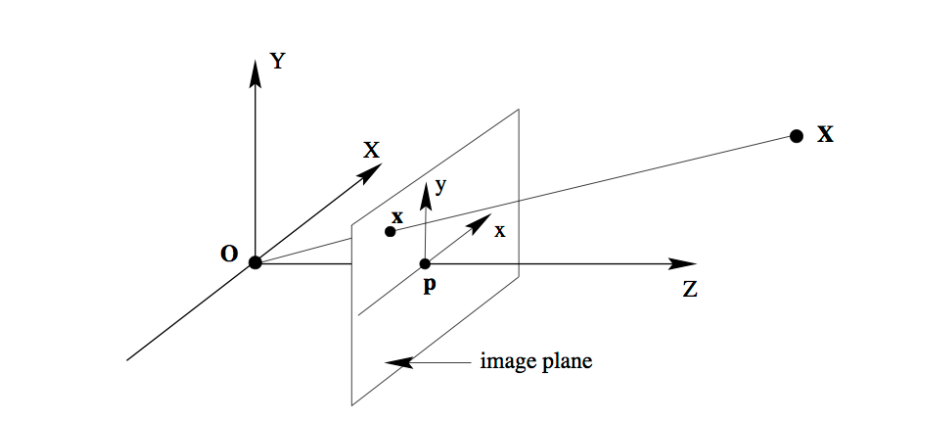
首先得了解物体在针孔相机模型下, 由世界坐标系投影到像素坐标系的数学模型。 图像中的像素坐标点 \(\mathbf{x}=\left[\begin{array}{l}x \\ y\end{array}\right]\) 和它在真实世界下的世界坐标点 \(\mathbf{X}=\left[\begin{array}{l}X \\ Y \\ Z\end{array}\right]\) 的对应关 系为:

\[\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\left[\begin{array}{lll} f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right]\left[\begin{array}{cc} \mathbf{R} & \mathbf{t} \\ \mathbf{0}^T & 1 \end{array}\right]\left[\begin{array}{c} X \\ Y \\ Z \\ 1 \end{array}\right] \]

用矩阵形式表示:

\[\mathbf{x}=\mathbf{K}[\mathbf{R} \mid \mathbf{t}] \mathbf{X} \]

或者:

\[\mathbf{x}=\mathbf{P X} \]

对于同一个世界坐标系下的点, 在多个相机坐标系下成像, 即为:

\[\begin{aligned} &\mathbf{x}_1=\mathbf{K}\left[\mathbf{R}_1 \mid \mathbf{t}_1\right] \mathbf{X} \\ &\mathbf{x}_2=\mathbf{K}\left[\mathbf{R}_2 \mid \mathbf{t}_2\right] \mathbf{X} \\ &\mathbf{x}_3=\mathbf{K}\left[\mathbf{R}_3 \mid \mathbf{t}_3\right] \mathbf{X} \end{aligned} \]

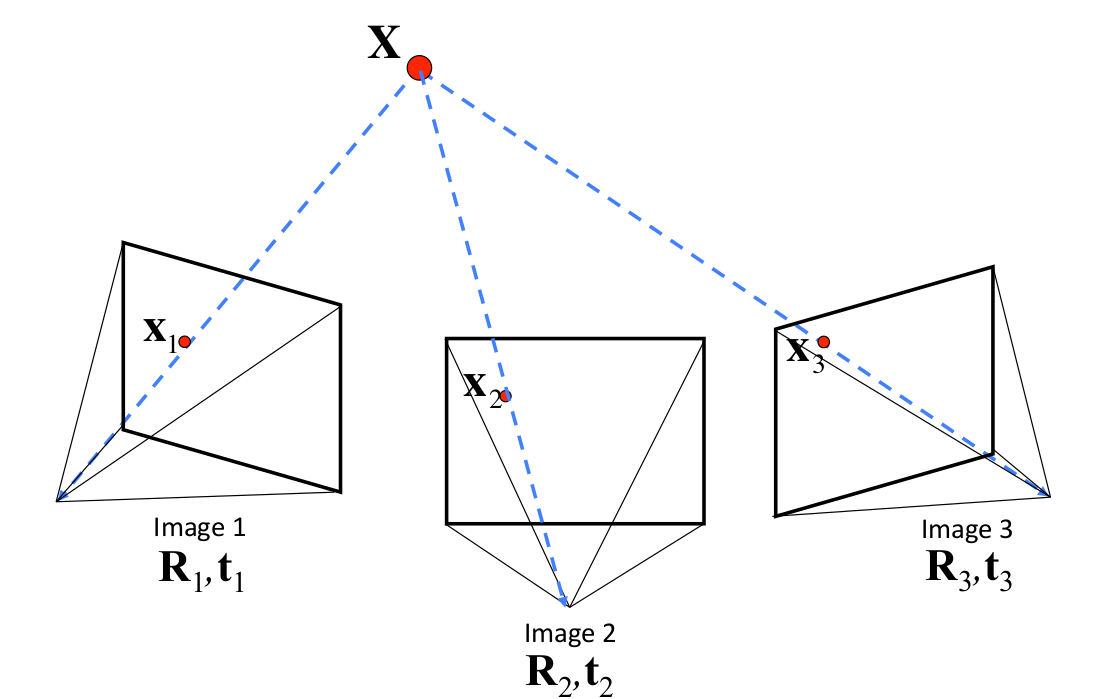
如果能准确找到这些对应点，就可以准确计算出各相机的R,t，但事实上只能用估计的方法求得较好的对应点。一个思路是提取各图像中物体的特征点，常用的算法是SIFT，因其具有尺度和旋转不变性，再去做匹配，再用RANSC算法优化改善匹配对。之后利用F矩阵和E矩阵可以算出相机的R,t，再通过三角化得到稀疏点云，如下图：

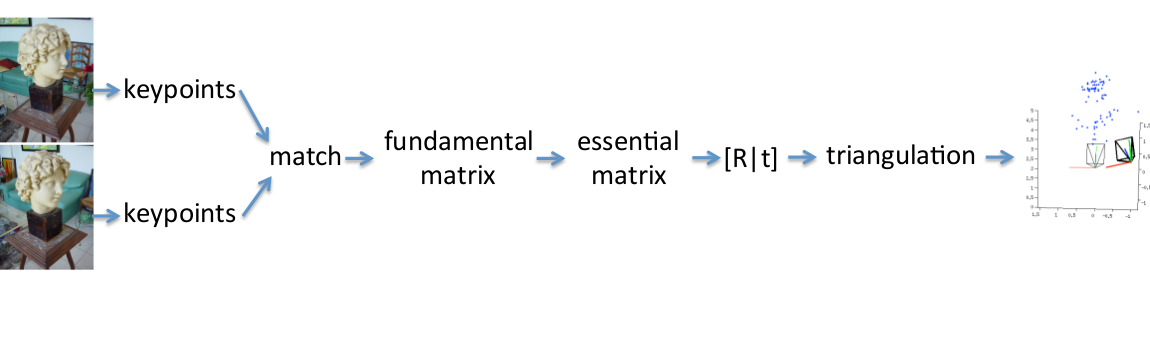
算法流程

特征点提取

特征点提取方法

• Shi&Tomasi

• SIFT

• SURF

特征点匹配

和建立track,图像对两两匹配,一般采用欧式距离.有两种方法：

• 粗暴匹配,对所有特征点都穷举计算距离
• 邻近搜索,建立KD树,缩小搜索范围,能提高效率,但也有可能不是最优,所以邻域取值是关键,越大越准确,越大计算量越大

然而初选的匹配对可能还是不可靠，需要用几何约束去检测。这个测试是基于事实的，假设一个静止场景，不是所有的匹配特征点在实际场景中是符合物理规律的。那么就需要计算对极几何，F矩阵可以把两张图片之间的像素坐标联系起来，并包含相机的内参信息。每一个符合的匹配对像素坐标都需要满足：

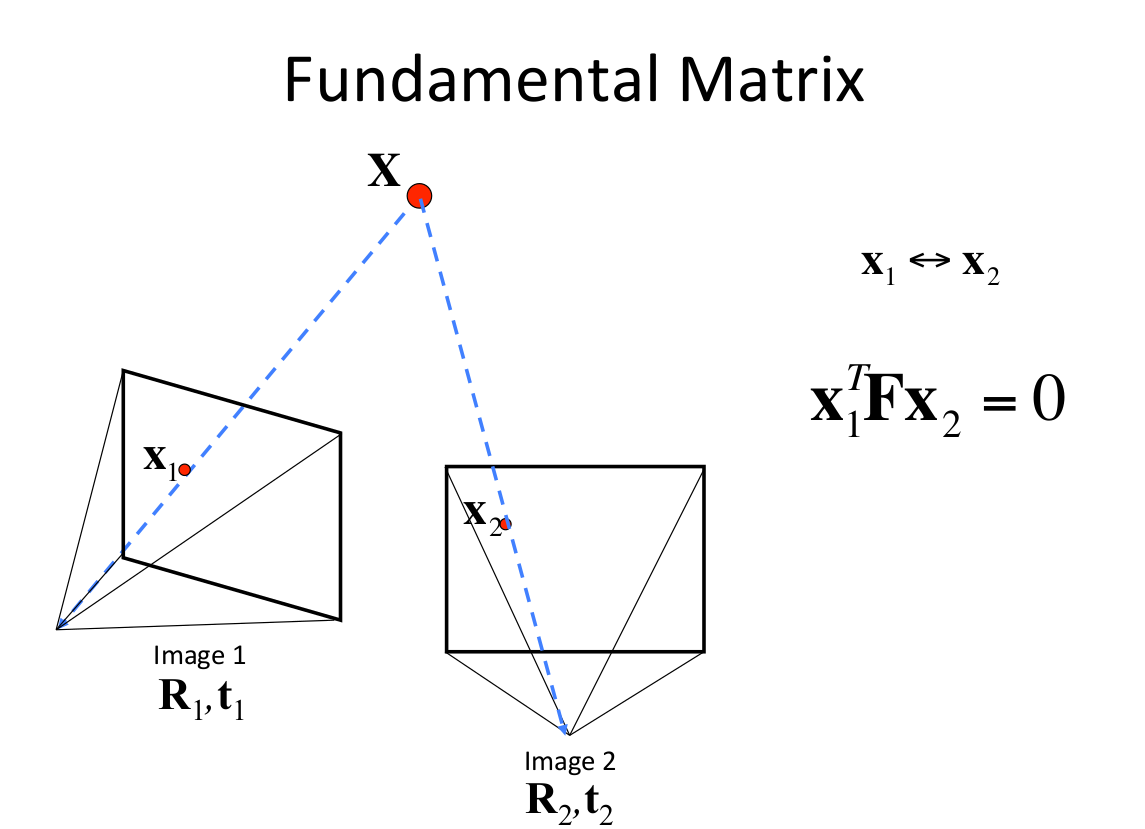
然而像这种F矩阵计算出有很多噪声数据，需要用RANSAC(随机抽样一致性)算法进行滤波，用直接线性变换(DLT)(需要八组对应点)来进行RANSACA假设，剔除不满足基础矩阵的匹配对。

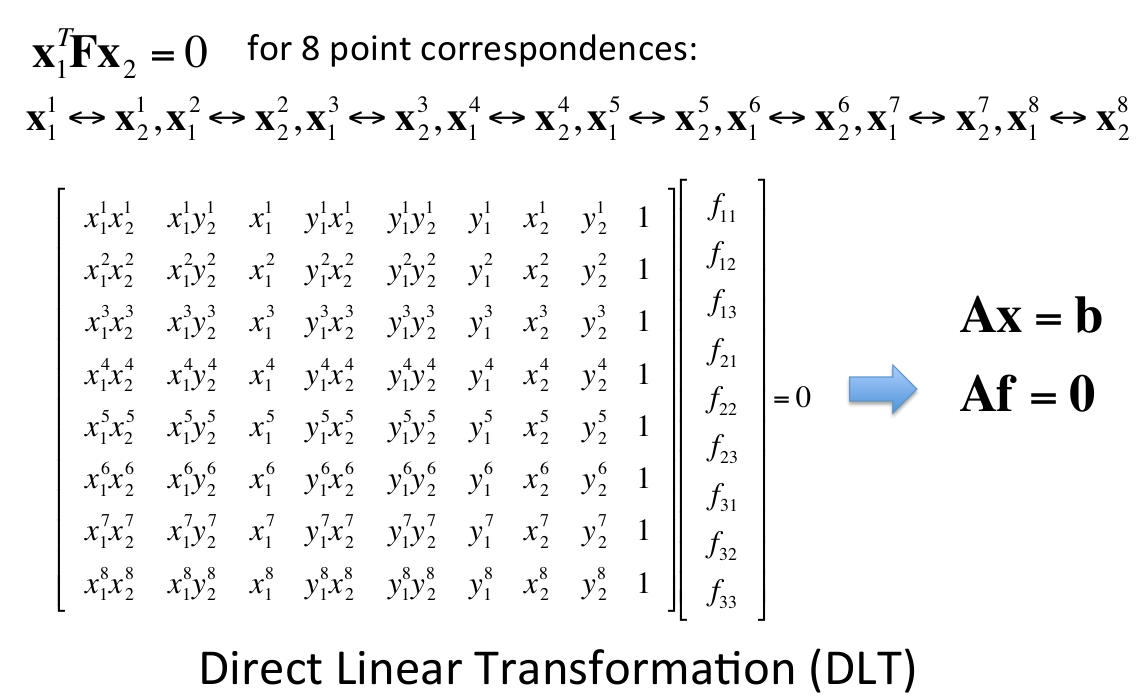
用RANSAC去估计基础矩阵F的思路是：

1. 多次迭代以下流程：
   • 选8个点
   • 用DLT算法计算F
   • 记录内点的数目
2. 选取内点最多的对应F

这时候可以找到比较好的匹配点对了。

本质矩阵估计

本征矩阵有7个独立参数
估计出本质矩阵的目的是为了对之前求得的匹配进行约束，得到的匹配成为几何一致匹配，不同图像上的几何一致匹配形成了一个TRACK（其实就是一个空间点在不同的图像上的投影点之间的匹配）。

本质矩阵分解为R和T

• SVD分解

• 存在4种可能的解，寻找正确的解

• 检查旋转矩阵R的正确性

  R的行列式必须为1或者-1

点云融合

由上面计算出来的 \(R, t\) 和相机内参, 可以恢复出物体的稀疏点云结构, 如何将点云 融合呢, 如果求出的 \(R, t\) 是一个准确解, 这时直接讲各部分点云通过 \(R, t\) 变换到同 一基准下就可以完成融合的过程。单上面求解出来的 \(R, t\) 仍然不够准确, 这时候可 以通过Bundle Adjustment (BA), 这是一个非线性优化的过程, 目的是使重建误 差降低到最小, 通过调整POSE和三维点使反向投影差最小, 如果相机没有标定, 还 应该将焦距也参与平差。BA最小化以下目标函数:

\[\min \sum_i \sum_j\left(\tilde{\mathbf{x}}_i^j-\mathbf{K}\left[\mathbf{R}_i \mid \mathbf{t}_i\right] \mathbf{X}^j\right)^2 \]

多幅图像的计算方法, 依次迭代上面的流程, 求得比较准确的 \(R, t\) 后, 即可进行点 云的融合, 到此完成稀疏点云的重建过程。

重投影

将三维点三角化并重映射到摄像机得到二维点，计算与最初二维点之间的距离，说明三角化误差。

计算第三个摄像机到到世界坐标系的变换矩阵(R和T)

假设：用于多目重建的图像是有序的，即相邻图像的拍摄位置也是相邻的。

个人猜想：

• 最简单的想法，就是沿用双目重建的方法，即在第三幅图像和第一幅图像之间提取特征点，然后估计本征矩阵E。那么加入第四幅、第五幅，乃至更多呢？随着图像数量的增加，新加入的图像与第一幅图像的差异可能越来越大，特征点的提取变得异常困难，这时就不能再沿用双目重建的方法了。
• 用新加入的图像和相邻图像进行特征匹配，然后计算E，但这是计算的是相对变换，比如相机三到相机二的变换，而我们需要的是相机三到相机一的变换。有人说，既然知道相机二到相机一的变换，又知道相机到三到相机二的变换，不就能求出相机三到相机一的变换吗？实际上，通过这种方式，你只能求出相机三到相机一的旋转变换（旋转矩阵R），而他们之间的位移向量T，是无法求出的。这是因为上面两个函数求出的位移向量，都是单位向量，丢失了相机之间位移的比例关系。

算法描述：

• 摄像机标定或摄像机之态估计，对于输入的第三幅图片，计算第三幅图片与第二幅图片的匹配点，这些匹配点中，肯定有一部分也是图像二与图像一之间的匹配点，也就是说，这些匹配点中有一部分的空间坐标是已知的，同时又知道这些点在第三幅图像中的像素坐标，即可计算变换矩阵。

• 透视N点法（PNP）
  三角化更多的点并查看这些点是如何融入存在的几何结构中，然后进行求解。

• 迭代最近点法（ICP）

更多摄像相机的变换矩阵计算

得到第三个摄像机的变换矩阵后，就可以计算匹配点的在空间中的坐标，得到三维点云，将新得到的三维点云与之前计算得三维点云进行融合（已经存在的空间点，就没必要再添加了，只添加在图像二和三之间匹配，但在图像一和图像三中没有匹配的点）。然后循环迭代，如下图所示。

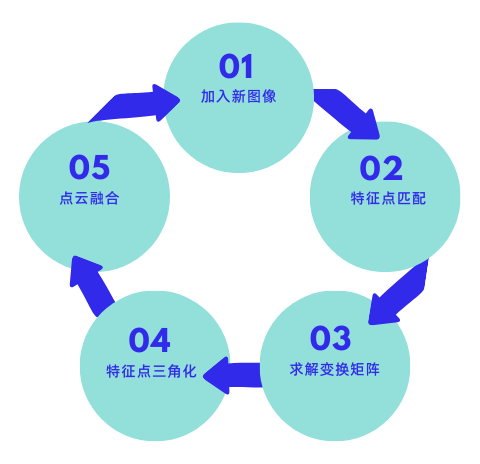
重构的细化与优化

原因：随着图像的不断增加，误差会不断累积，最后误差过大以至于完全偏离重建的目标。

目的：三维点云的位置和摄像机的位置优化

基于SFM算法的无人机校园三维建模具体流程

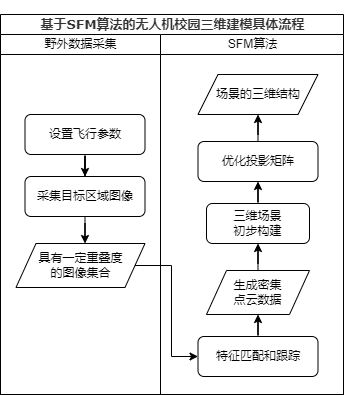
问题与思考

模型外观与组成分析

得到研究区域的初步模型如下图所示：

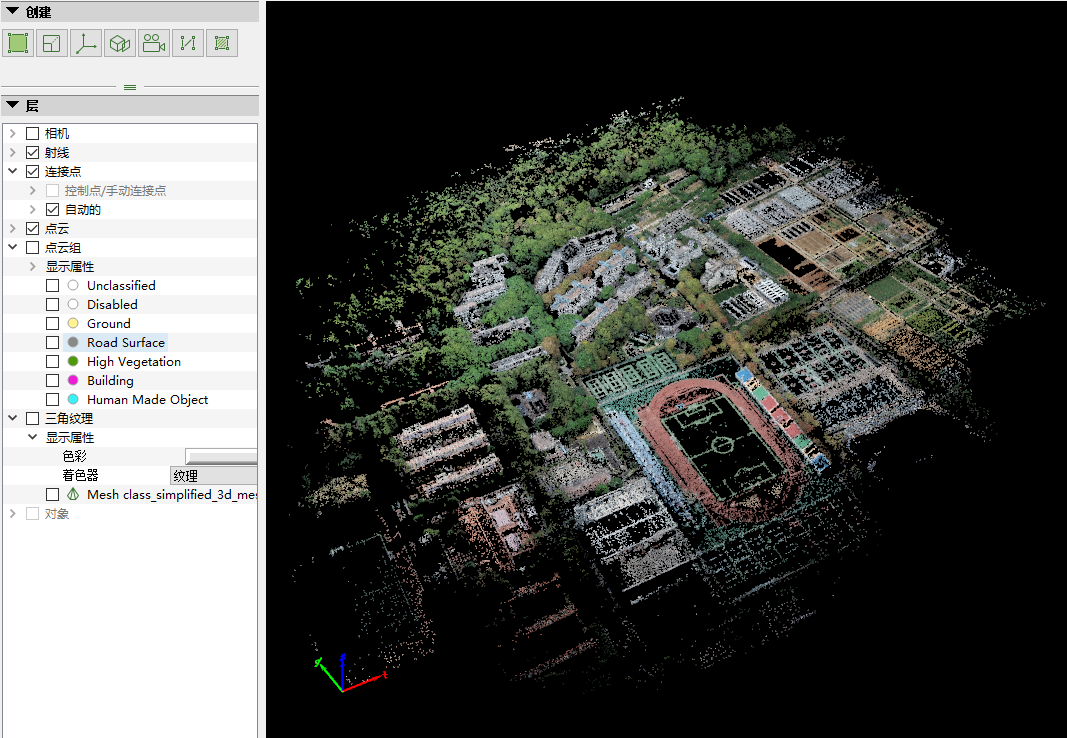
其中，可以看到此时未显示出真正的完全模型外观，而是由较为稀疏的点云所组成的表面。将其放大后可以看到高低不同、错落有致的点云所组成的简化模型外观。

添加点云组，得到结果如下图所示。

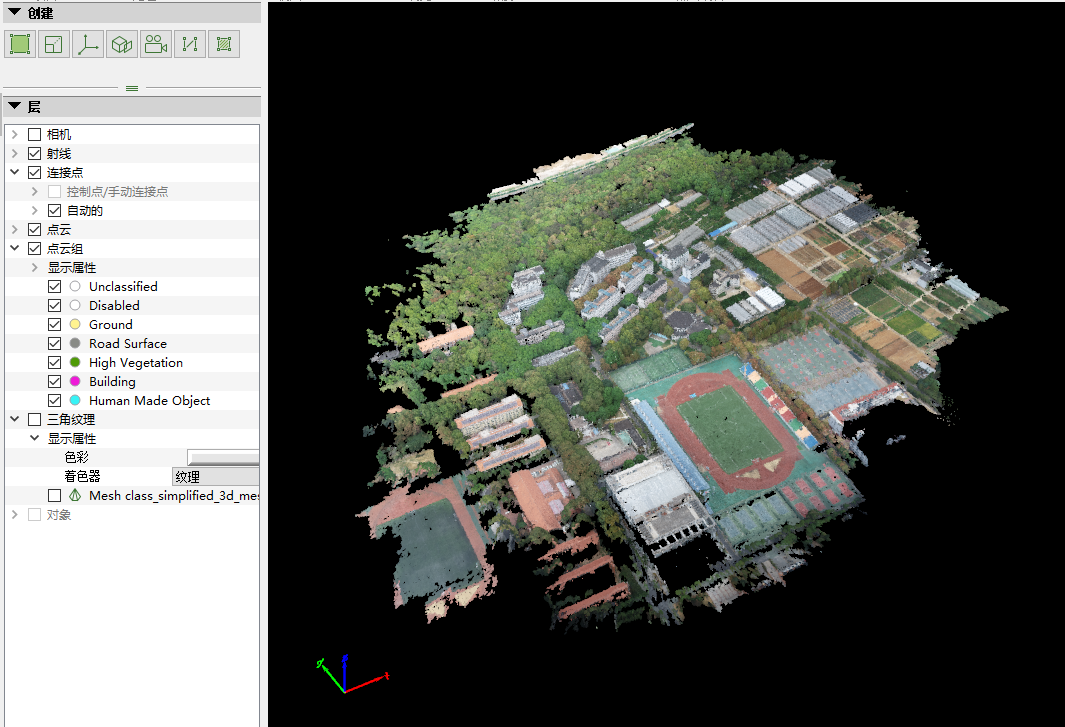
对比上述二者结果，可以发现前者以稀疏点云表示了平面信息（如地面、楼房顶面等），且表示得并不是很充分，仅可以大致刻画出某平面所处在的位置，而无法展示其具体外观与纹理；而后者则将各类物体表面的一些凸出细节（如地面的汽车与树木、楼房顶面的设备与侧面凸出的窗檐等）展示出来，并进一步突出了不同地物的颜色与部分纹理特征（如操场跑道与足球场、汽车颜色、远处东运动场不同颜色的观众席等）。

添加三角纹理，如下图所示。

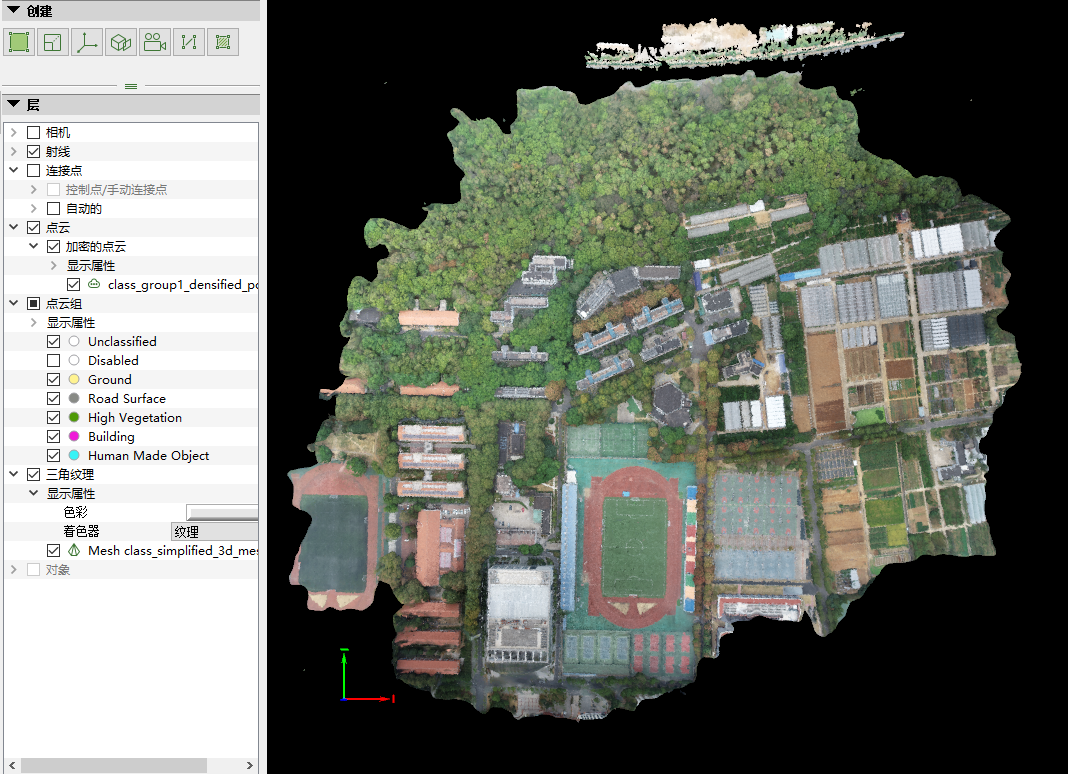
由此即显示出完整模型，同样由此可以看出模型所存在的问题——侧面的外形与纹理与实际地物相差较大。

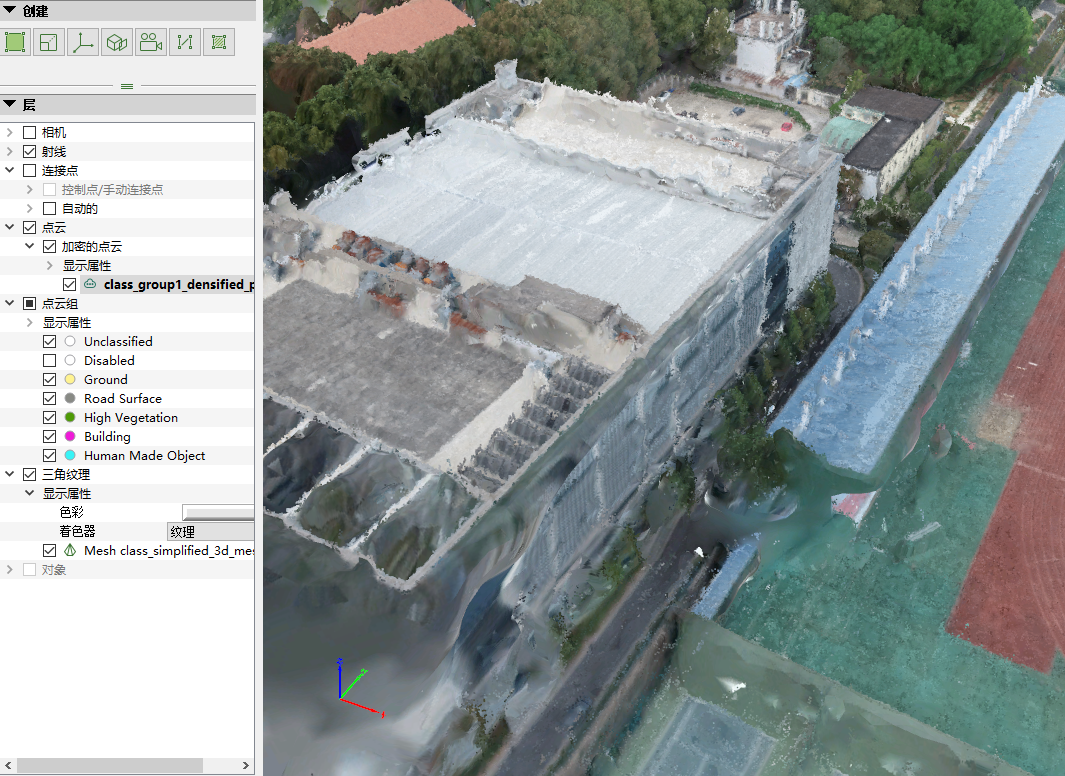
模型部分外形与纹理错误分析

得到模型后，可以看到部分地物在外形或纹理方面具有明显的扭曲、模糊等错误，如下图所示。

对外形、纹理均较为良好的位置与外形、纹理均存在一定问题位置加以分析。选中外形符合实际、纹理清晰位置的区域，可以发现这些区域与多张无人机航拍影像相连，纹理信息比较充足。

查看外形扭曲、纹理模糊的区域，可以发现这些地方基本都缺少图像。由此可以推测，由于纹理是在模型搭建完毕后贴于地物表面，纹理的来源于原图像，没有图像的地方的纹理由软件自动生成，导致纹理的错乱，由于无人机飞行高度较高，地物侧面位置或被其它地物遮挡位置的信息获取不足；若需对上述异常问题加以修复，需要在后期对地物其它角度信息加以拍摄、获取。

模型质量报告分析

得到模型后，同时会得到一篇内容丰富的模型质量报告（Quality Report）。

首先，对于“Summary”模块，如下表所示。

在这个部分，可以看到模型的基本情况。结果的平均地面采样点距离（Average Ground Sampling Distance)为3.26 cm。研究区域模型占地面积为0.400km2。

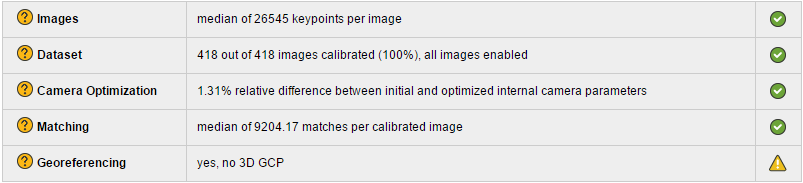
对于“Quality Check”模块，如下图所示。由“Dataset”部分可知，所选研究区域418张无人机航拍影像中有418张完成定标并参与后续操作。由“Camera Optimization”部分可知，原始相机内部参数与优化后的相机内部参数具有1.31%的相对误差。

对于“Calibration Details”模块，在“Initial Image Positions”部分可以得到无人机影像的位置信息，如下图所示。

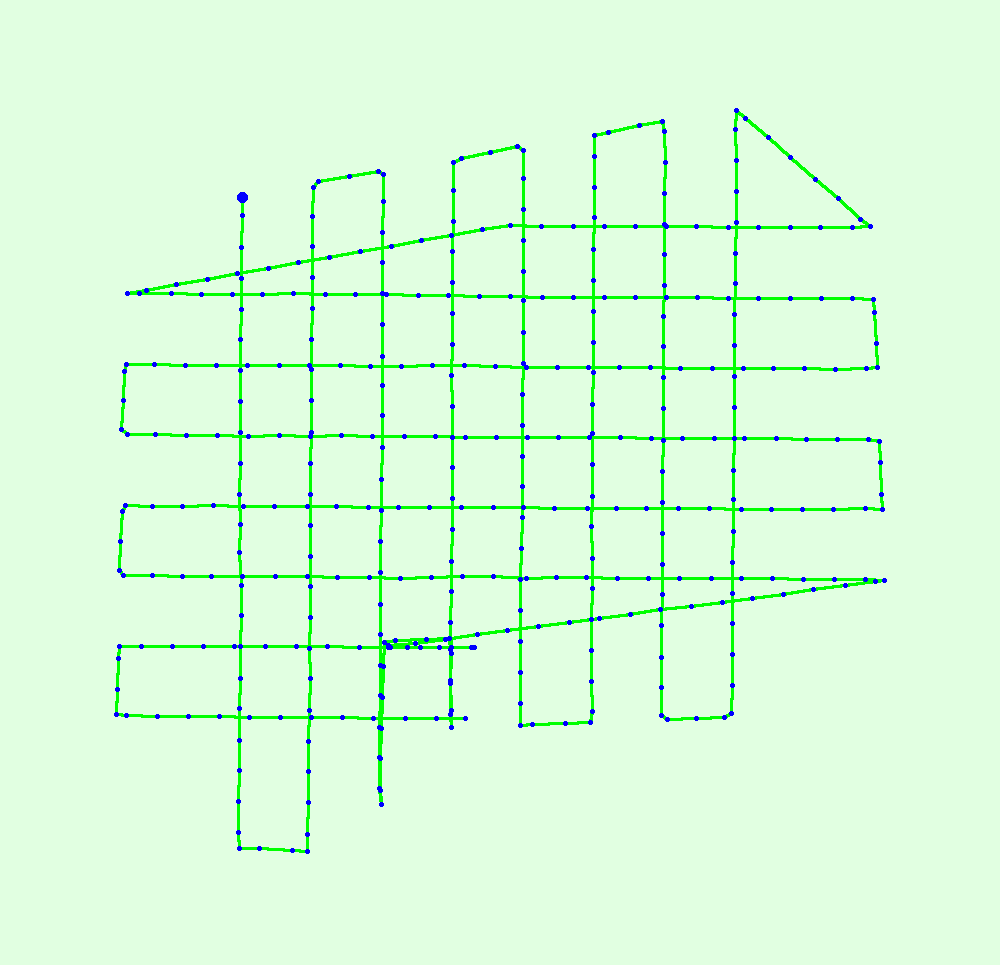
在“Computed Image/GCPs/Manual Tie Points Positions”部分，看到出现问题的影像在哪一部分，如下图所示。在本次实验中，没有出现问题的图片。

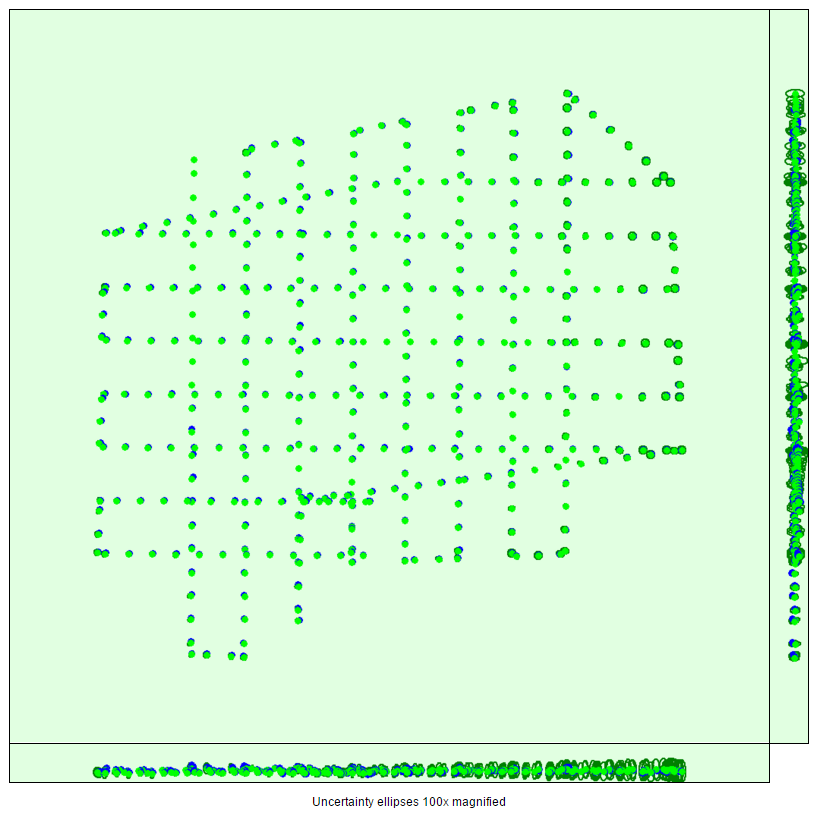
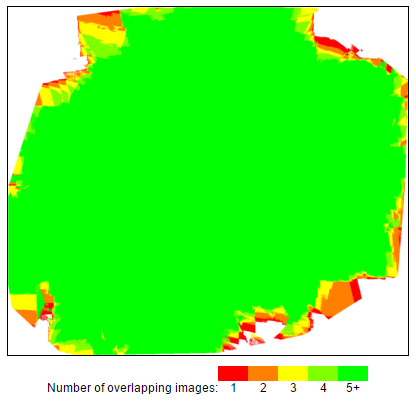
在“Overlap”部分，该部分为重叠度分布图，可以直观地看到出现问题的影像在哪一部分，红色的部分即为重叠度还不够的区域，这些区域需要复飞。

对于“Bundle Block Adjustment Details”模块，得到空中三角测量中误差（Mean Reprojection Error）为0.132，如下图所示。这一误差的单位为像素（pixels），则其所代表的物理长度单位即为0.132乘以像素代表的真实长度。

下图表示计算出的图像位置与匹配图像之间的链接。链接的明暗度表示图像之间匹配的二维关键点的数量。明亮的链接表示弱链接，需要手动绑点或更多的图像。深绿色的椭圆表示捆绑块调整结果的相对相机位置不确定性。

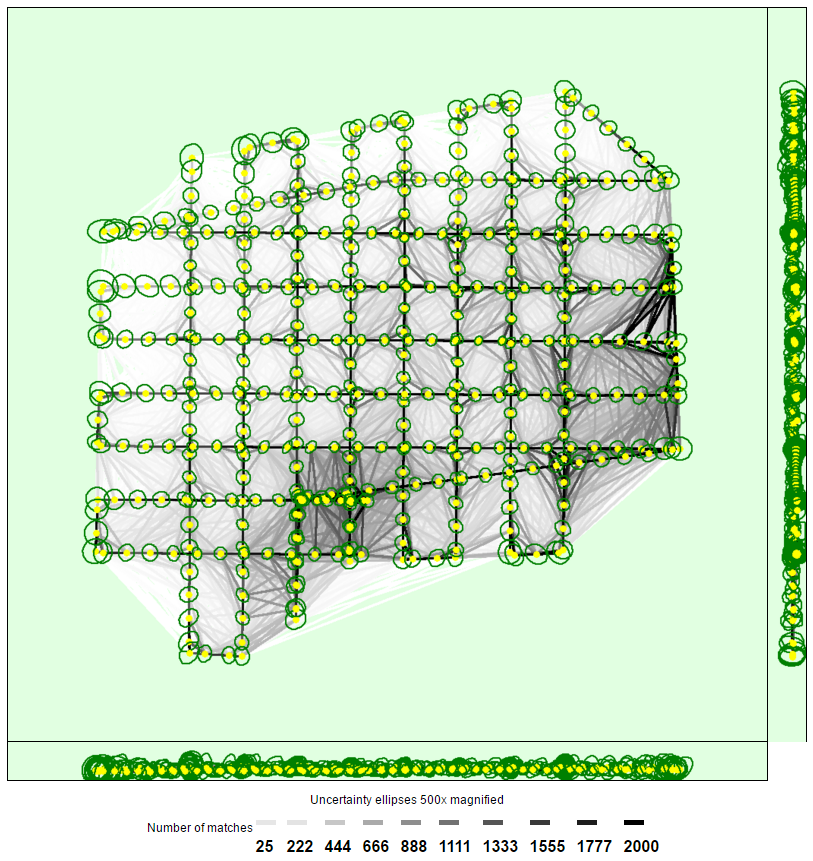
在图像中找到的每个特征点称为一个关键点。当发现两个不同图像上的两个关键点相同时，它们是匹配的关键点。每组正确匹配的关键点将生成一个 3D 点。这些特征检测进程和关键点匹配在步骤 1 中进行。

模型边界缺失问题

可以看到，在所得三维模型边缘位置，往往会出现不规则的模型缺失，如下图所示。

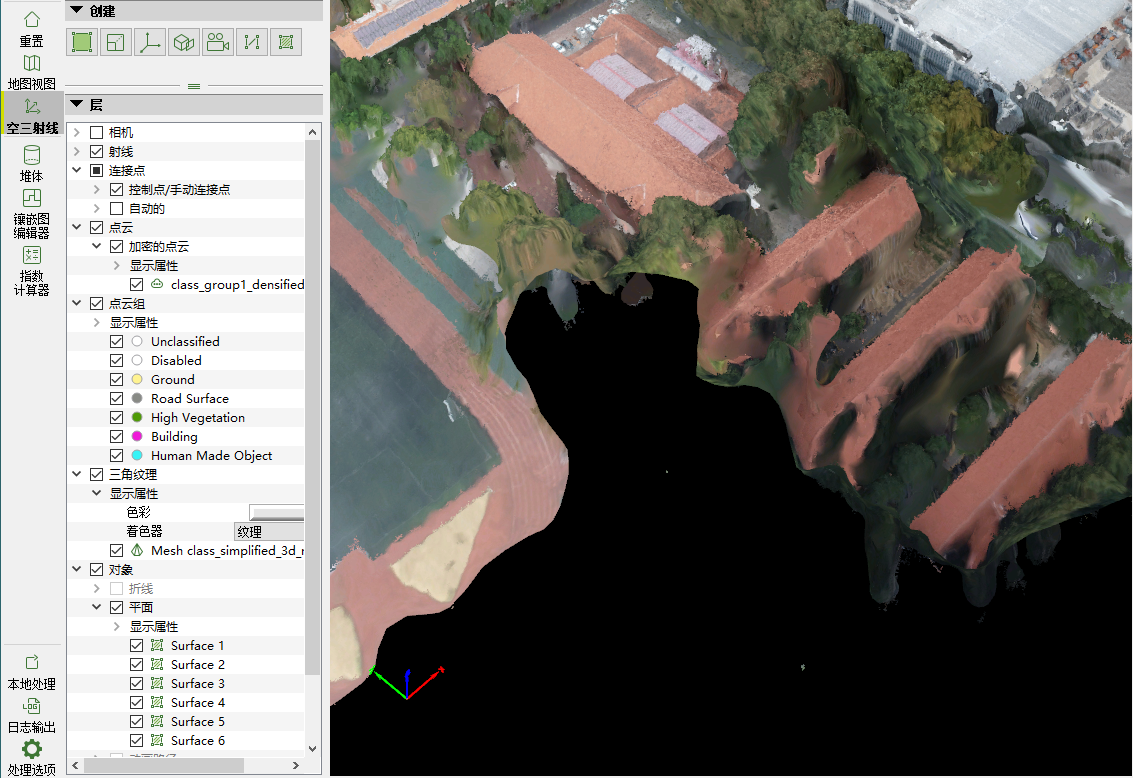
针对这一问题，个人认为是由于：在现实场景中，临近研究区域边界的点，所对应无人机影像数量较少（例如研究区域最南侧的地物，仅有其北侧的无人机影像，而处于研究区域中心位置的地物则有多角度的无人机影像，所以出现边界缺失的原因我认为是由于对其不同角度的描述信息较少，不足以依据这些信息对其空间三维位置加以恢复，导致这部分地区无法建模。