第04次作业-树

1.学习总结

1.1树结构思维导图

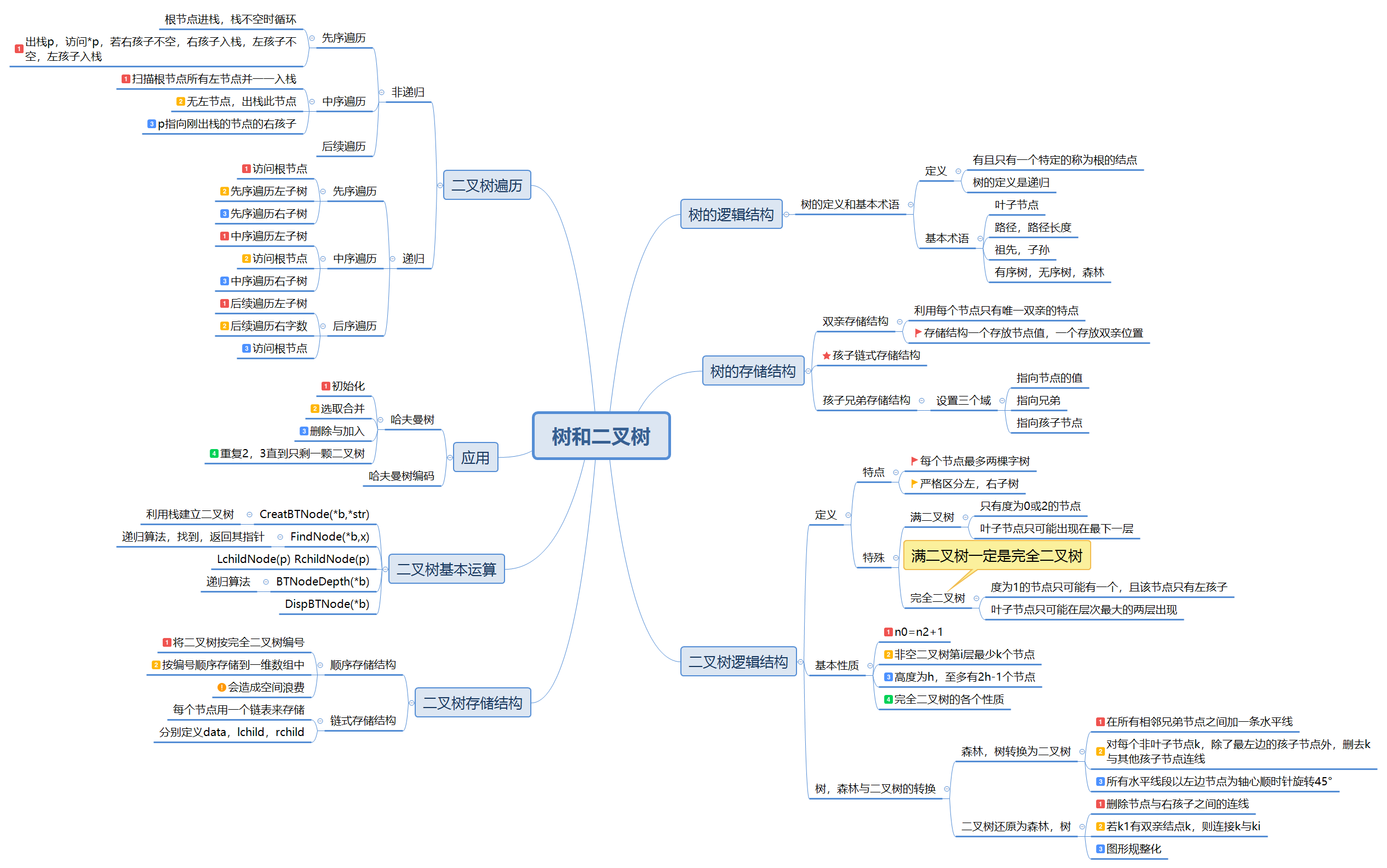
1.2树结构学习体会

1)树的结构：非线性结构，也是递归型的结构，属于集合之间的关系。
2树和二叉树是难点，但着实是重点,树的一些基本计算公式应牢记。
3)课本递归好理解，真正自己写的时候总是无从下手，PTA更需多加练习。
4)学完树，更加体会到写代码之前学写伪代码的重要性。

2.PTA实验作业

题目一:6-4 jmu-ds-表达式树（25 分）

2.设计思路：

/*建表达式二叉树*/
定义树栈 s1 存储数字
定义字符型栈 s2 存储运算符
‘#’入栈s2；/*作为标记*/
while 字符串不空
    if str[i] 为数字
      then 创建树节点，此节点赋予str[i]的值，并置其左右孩子为空后再次入栈s1；
    else 
      调用Precede函数
      if ‘<’
        then 运算符入栈s2；
      if'='
        then s2栈顶元素出栈
      if'>'
        then 创建新的树节点并赋予s2栈顶元素值，右左孩子分别取s1栈顶元素后再次入s1栈；
          end
while 栈s2中仍有运算符
    创建新的树节点并赋予s2栈顶元素值，右左孩子分别取s1栈顶元素后再次入s1栈；
      end
/*计算表达式树*/
定义浮点型数 a b 存储运算数；
利用递归把所有字符转换成数字；
a，b分别存储树节点的左右子树；
while 树节点存在
    if '+'
      then 返回 a+b；
    if'-'
      then 返回 a-b；
    if'*'
      then 返回a*b；
    if'/'
      then if b不为0
         返回a/b；
  
      

3.代码截图




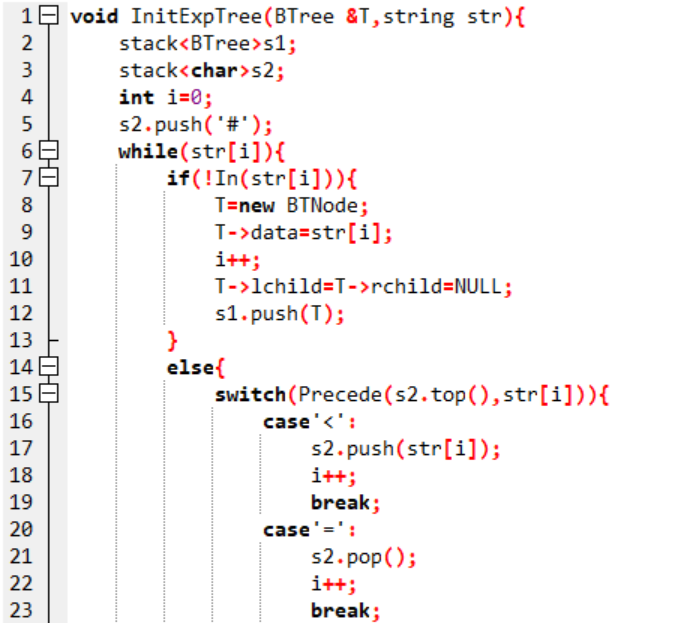
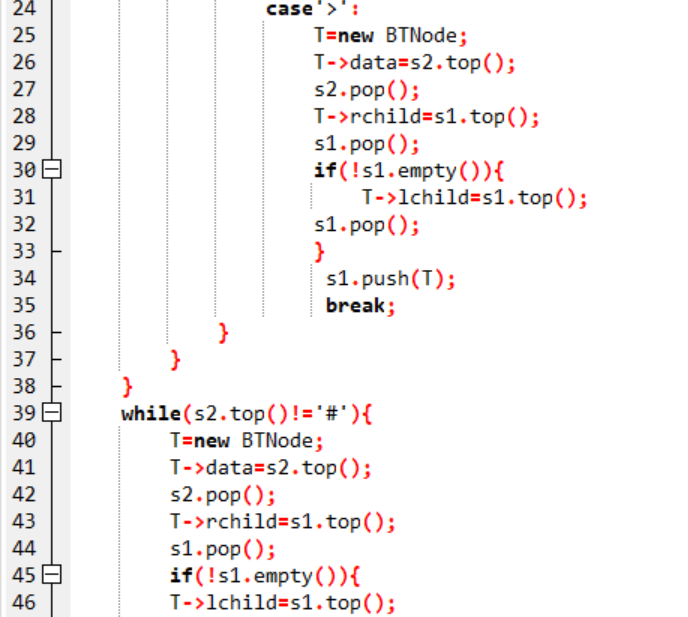
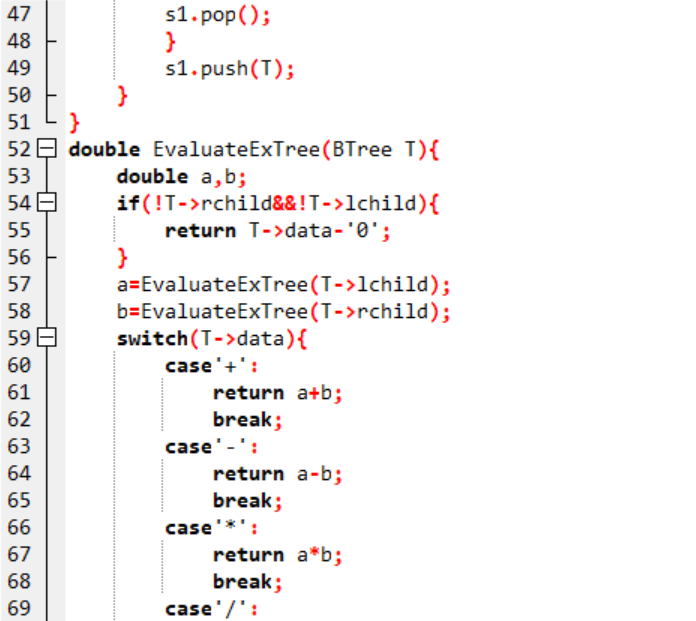
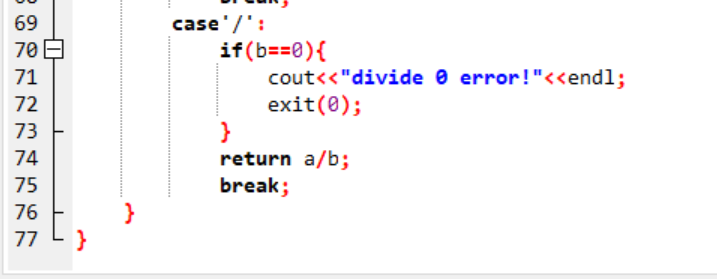
4.PTA提交列表说明

• 多种错误：没有将‘#’入栈
  解决方法：期初就要将‘#’入栈起到做标记的作用
• 多种错误：粗心大意把a*b打成了a-b
  解决方法：修正a*b
• 多种错误：没有考虑遍历完字符串后运算符栈中还存在运算符的可能
  解决方法：多一个while判断语句

while(s2.top()!='#'){
		T=new BTNode;
		T->data=s2.top();
		s2.pop();
		T->rchild=s1.top();
		s1.pop();
		if(!s1.empty()){
		T->lchild=s1.top();
		s1.pop();	
		}
		s1.push(T);
	}

---

题目二:6-1 jmu-ds-二叉树操作集（20 分）

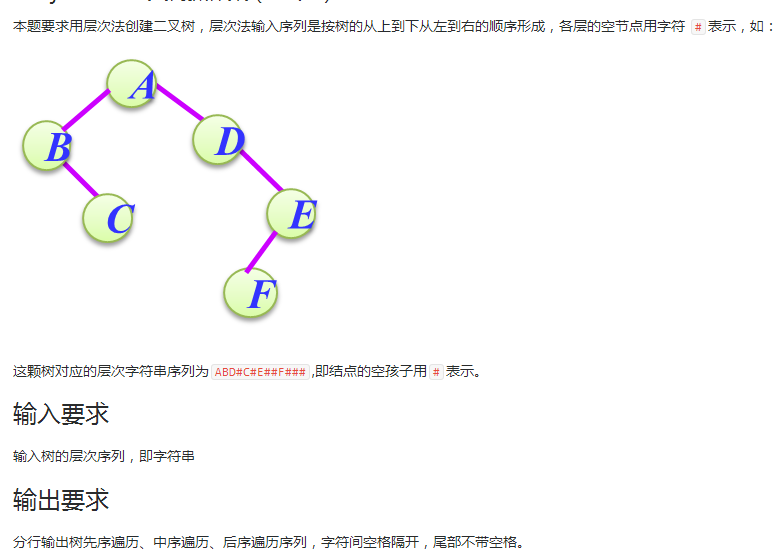
2.设计思路：

/*根据层次字符序列创建二叉树*/
定义树型指针 *T;
定义树形队列 Q；
if str[0] 非空
  then 创建 BT 新节点，并赋予值str[0]；
      BT左右孩子都置空；
      BT入队；
while 队列非空
     队头元素出队并赋予T；
     if str[++i] 为‘#’
       then T的左孩子节点置为空；
     else
        T的左孩子节点赋予元素str[++i]的值；
    T的左孩子的左孩子右孩子分别置于空；
    T的左孩子入队；
if str[++i] 为‘#’
       then T的右孩子节点置为空；
     else
        T的右孩子节点赋予元素str[++i]的值；
    T的右孩子的左孩子右孩子分别置于空；
    T的右孩子入队；
      end

3.代码截图

4.PTA提交列表说明

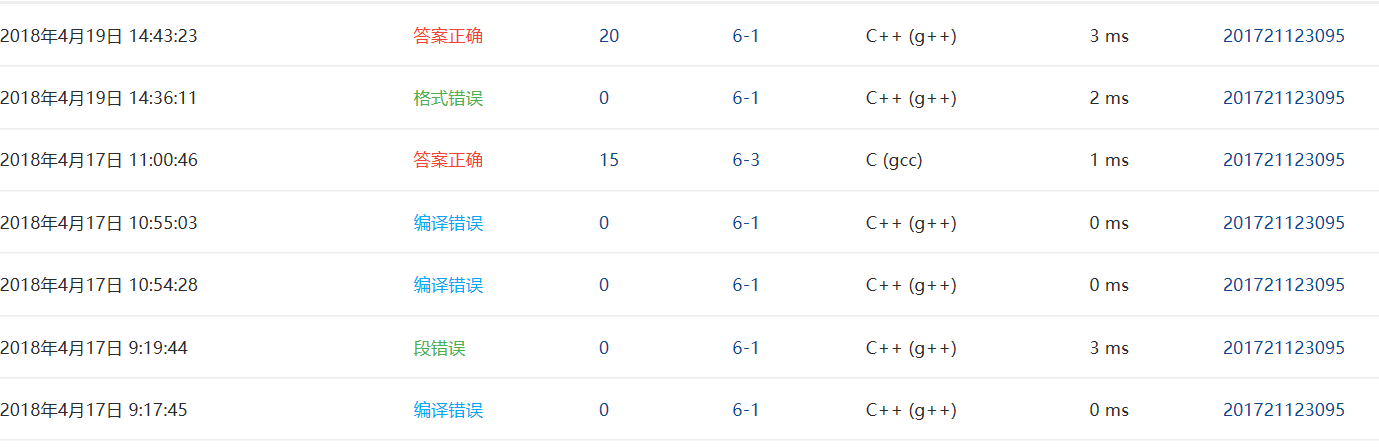
• 段错误：不知道如何建树，左右孩子节点遍历完后如何遍历下一节点
  解决方法：利用队列，左右孩子判断完便入队，下一次循环队列元素出队，即指向节点的左孩子，以此类推。
• 格式错误：题目要求所有递归遍历输出都要带有空格
  解决方法：递归遍历的同时输出空格，eg：

if(BT->lchild){
		cout<<" ";
		PreOrder(BT->lchild);
	}
	if(BT->rchild){
		cout<<" ";
		PreOrder(BT->rchild);
	}

---

题目三：7-8 jmu-ds-二叉树叶子结点带权路径长度和（25 分）

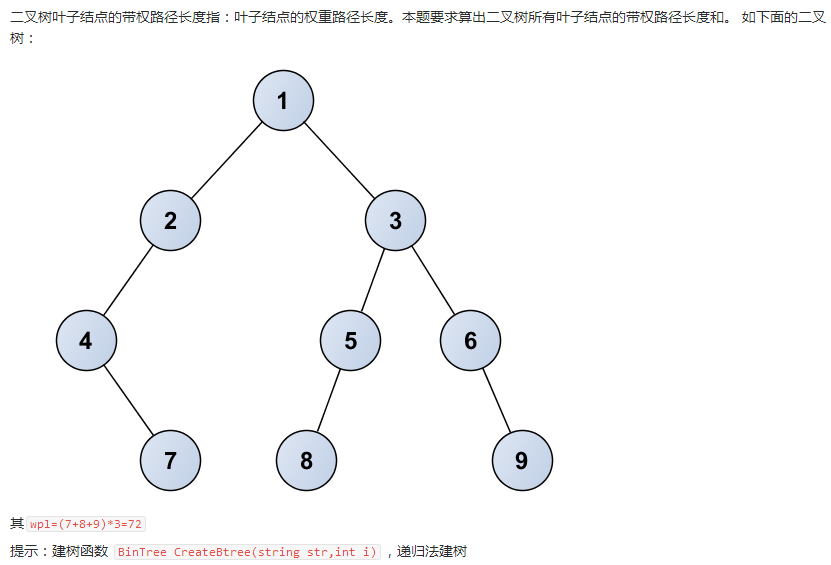
2.设计思路：

/*创建树*/
定义链表 str 存储输入的字符
定义树形指针 *bt
利用getchar（）把输入的第一个字符吃掉
其余字符存储到 str 中；
while str[i++] 不为'#'
      then 建立新树节点bt；
       将str[i]的值赋予bt；
       依次递归遍历bt的左子树和右子树；
          end
/*求叶子节点带权路径长度和*/
定义整型字符 h 存储叶子节点所在的高度
定义整型字符 s 存储运算结果
if bt的左右孩子节点都为空
  then bt节点字符数转换为数字a；
      s+=a*高度；
if bt的左孩子节点不为空||bt的右孩子节点不为空
  then 采用递归遍历查找出叶子节点；

3.代码截图

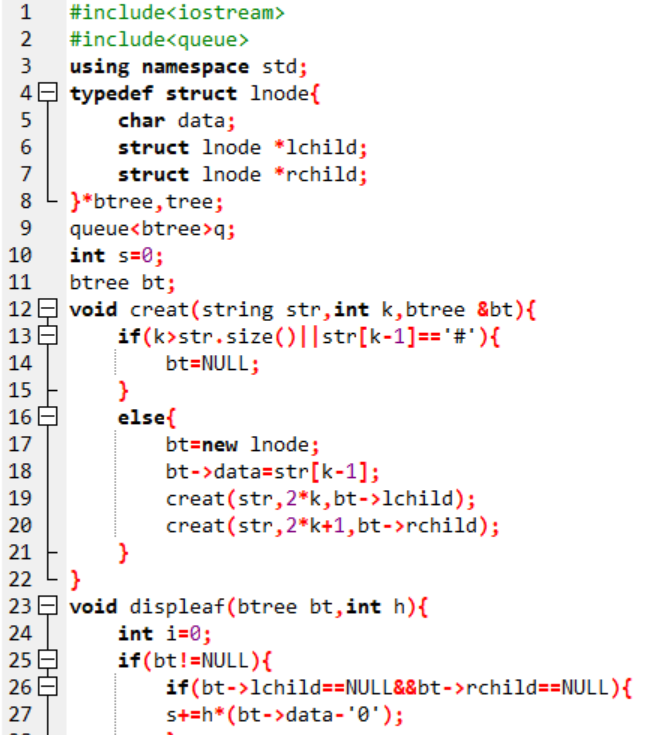
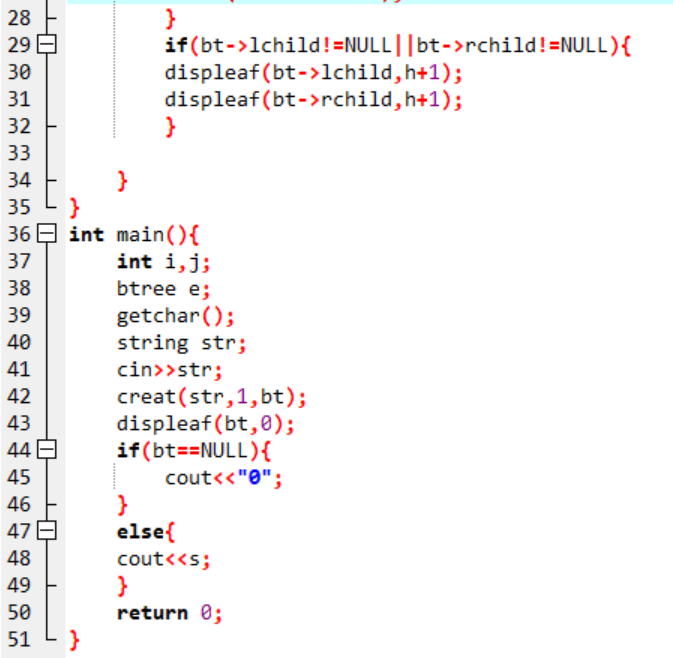
4.PTA提交列表说明

• 部分正确：忘记树存储的是字符而不是数字
  解决方法：每一个data值都要转换为数字，即s+=h*(bt->data-'0');
• 部分正确：只考虑了特殊情况：叶子节点都在最后一层，导致编译一直只通过测试点0
  解决方法：在每一次找出来叶子节点时，都要实时更新其所处的高度

3.PTA最后排名

3.1PTA排名截图

3.2我的总分
2分

PTA总分在180--230分：2分（必做题大部分做完）

4.阅读代码

题目：计算二叉树的最大宽度
1)思路：

先创建一个队列，用一个标注变量去标注最开始时队尾的位置，然后用一个循环来操作二叉树，循环体内的操作和层序遍历类似，不同的是，在每趟循环结束后都要来判断上一层是否便利完成（用那个标注变量和队首的位置比较）如果便利完成，则刷新最大宽度。

具体代码实现：

typedef struct TreeNode *BinTree;  
struct TreeNode  
{  
   int Key;  
   BinTree  Left;  
   BinTree  Right;  
};  
int Width( BinTree T )  
{  
   BinTree  p;  
   Queue Q;  
   int Last, temp_width, max_width;  
   temp_width = max_width = 0;  
   Q = CreateQueue(MaxElements);  
   Last = Queue_rear(Q);//标注队尾位置  
   if ( T == NULL) return 0;  
   else   
 {  
      Enqueue(T, Q);//将二叉树的树根入队列  
      while (!IsEmpty(Q))   
   {  
         p = Front_Dequeue(Q); //由队头出队列一个元素     
         temp_width++;  
         if ( p->Left)  Enqueue(p->Left, Q);//将出队列的这个元素的左孩子节点入队  
         if (p->right)  Enqueue(p->right, Q);//将出队列的这个元素的右孩子节点入队  
         if ( Queue_front(Q) > Last ) //判断上一层是否遍历完  
        {  
            Last = Queue_rear(Q);//更新标注变量的值  
            if ( temp_width > max_width ) max_width = temp_width;               
            temp_width = 0;   
         } /* end-if */  
      } /* end-while */  
      return  max_width;  
   } /* end-else */  
}  

2)优点：借助“数量标注”，设置一个变量来标定你这一层的节点的数量，利用队列入队和出队时队列的队头与队尾位置关系的变化关系来达成分隔二叉树层次的作用。
3)代码相关地址:https://gitee.com/tanghuan5678/Data-Struct/commit/09d8fce3a241fdaab5e0e1ad53918c9dba22c214

5.代码Git提交记录截图