Cryptography | 密码学课程笔记 | 一次密码本

definition

一个三元组定义了密码的环境 ——（K, M, C）

• K：key space, a set of all possible keys
• M：a set of all possible messages
• C：a set of all possible ciphertexts

密码本身是一对算法E和D。（E, D）

• 加密算法 E(K,M) = C
• 解密算法 D(K,C) = M

一次性方程

密码必须满足一致性方程（算法一致，密钥一致，否则无法解密）

任意m∈M, k∈K ,
D(k,E(k,m)) = m

Tips

1.加密算法随机生成密钥（总是随机算法），解密算法的密钥和密文总是一致的（确定算法）

2.算法的效率

• 多项式时间内完成，取决于输入的规模
• 特定时间内完成

一次性密码本（The One Time Pad ）

加密： C = E(K,M) = K⊕M

msg	0 1 1 0 1 1 1
k	1 0 1 1 0 0 1
c	1 1 0 1 1 1 0

解密： M = D(K,C) = D(K,E(K,M)) = K⊕(K⊕M) = K⊕K⊕M = 0⊕M = M;

k	1 0 1 1 0 0 1
c	1 1 0 1 1 1 0
msg	0 1 1 0 1 1 1

由此可见，一次性密码本满足一次性方程，是密码！

Tips: K = M⊕C

如何推导？
C = K⊕M => C⊕M = K⊕M⊕M => C⊕M = K

OTP算法评价
优点：安全
确定：密钥太长

密码安全性

香农的贡献一

任何明文(M1,M2...)经过加密后生成C的概率都一样，就是完美安全密码。
从密文来看，我们无法得知C背后的明文是哪一个，因为概率都相等啊！

OTP has perfect secrecy!

proof:
E(K,M) = C  
=>  K⊕M = C
=> K = C⊕M = M⊕C  
=> #{k ∈ K:E(k,m) = c} = 1 
//满足E(k,m) = c的密钥只有一个！
对于一次性密码本OTP，没有惟密文攻击！（因为给了密文也没用，参照香农的定义~）

香农的贡献二

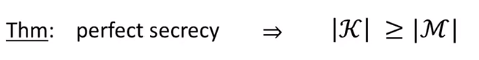
完美安全的密码，密钥的长度不小于明文的长度