套用解题模板---对背包问题的三种类分类
目录
对背包问题的三种类分类
1.排列组合问题

518. 零钱兑换 II (完全背包+顺序无关)
物品的数量是无限的
明确问题的性质
- 背包问题
- 组合问题(顺序是无关的)
- 完全背包问题(可以重复选择num)
组合问题:
dp[i] += dp[i-num]完全背包 且 顺序无关: nums在外 target在内

class Solution {
public int change(int amount, int[] coins) {
int n = coins.length;
int[] dp = new int[amount + 1];
dp[0] = 1;
for (int num : coins) {
for (int i = 1; i <= amount; i++) {
if (i >= num) {
dp[i] += dp[i - num];
}
}
}
return dp[amount];
}
}
494. 目标和(0-1背包+顺序无关)

明确问题的性质
- 背包问题
- 组合问题(顺序没有影响)
- 0-1背包问题(每个num只能使用一次)
组合问题:
dp[i] += dp[i-num]0-1背包问题,且,是组合问题(顺序不影响) nums在外, target在内,且target倒序循环
把所有符号为正的数总和设为一个背包的容量,容量为x;
把所有符号为负的数总和设为一个背包的容量,容量为y。
在给定的数组中,有多少种选择方法让背包装满。
令sum为数组的总和,则x+y = sum。
而两个背包的差为S,则x-y=S。(S已知)从而求得x=(S+sum)/2。
基于上述分析,题目转换为背包问题:给定一个数组和一个容量为x的背包,求有多少种方式让背包装满。
class Solution {
public int findTargetSumWays(int[] nums, int S) {
int sum = 0;
for (int num : nums) {
sum += num;
}
if (S>sum || (S+sum)%2==1) return 0;
int target = (S + sum) / 2;
int[] dp = new int[target + 1];
dp[0] = 1;
for (int num : nums) {
for (int i = target; i >= 0; i--) {
if (i >= num) {
dp[i] += dp[i - num];
}
}
}
return dp[target];
}
}
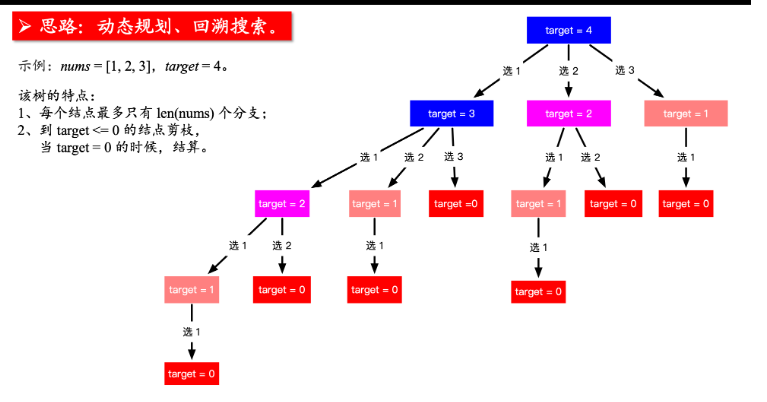
377. 组合总和 Ⅳ (完全背包+顺序有关)
先给这道题定性
- 背包问题
- 排列问题(先后顺序是有影响的)
- 完全背包问题(可以重复选用同一个数字)
排列问题:
dp[i] += dp[i-num]完全背包问题:且是 排列问题(顺序有关)
target在外, nums在内

public int combinationSum4(int[] nums, int target) {
// 状态 选择 dp base case
int[] dp = new int[target + 1];
dp[0] = 1;
for (int i = 1; i <= target; i++) {
for (int num : nums) {
if (num <= i) {
dp[i] = dp[i] + dp[i - num];// 上一个num选择下的组合可能数+这个num选择下可能的组合个数
}
}
}
return dp[target];
}
2.True、False问题公式

416. 分割等和子集(0-1背包 + 顺序无关)

可以使用动态规划解决
也可以使用 回溯+剪枝
明确问题性质
- 可以是背包问题
- 组合问题(顺序不影响)
- 0-1背包问题(num不可重复使用)
组合问题:
dp[i] = dp[i] || dp[i-num]0-1背包 且 组合: nums 在外循环, target在内循环 且 逆序
public boolean canPartition(int[] nums) {
int sum = 0;
for (int num : nums) sum += num;
// sc
if (sum % 2 != 0) return false;
int target = sum / 2;
boolean[] dp = new boolean[target + 1];
dp[0] = true;
for (int num : nums) {
for (int i = target; i >= 0; i--) {
if (i >= num) {
dp[i] = dp[i] || dp[i - num];
}
}
}
return dp[target];
}
139. 单词拆分 (完全背包+顺序有关)

给问题定性
- 是背包问题(target是字符串s, nums是字典列表)
- true false 问题(且 顺序是有关的,同一个单词前后顺序是有影响的)
- 完全背包(num可以重复选取)
排列问题: dp[i] = dp[i] || dp[i-num]
完全背包 且 顺序有关: target在外循环 nums在内循环
public class Number39_wordBreak {
// true false 问题
// 完全背包问题
// 顺序有关
public boolean wordBreak(String s, List<String> wordDict) {
int target = s.length();
boolean[] dp = new boolean[target + 1];
dp[0] = true;
for (int i = 1; i <= target; i++) {
for (String word : wordDict) {
int len = word.length();
if (i >= len && word.equals(s.substring(i - len, i))) {
dp[i] = dp[i] || dp[i - len];
}
}
}
return dp[target];
}
}
3.最大最小问题公式

322. 零钱兑换 (完全背包+顺序无关)
明确问题性质
- 背包问题 (target nums)
- 最大最小值问题
- 完全背包问题(顺序无关)
最大最小值问题:
dp[i] = min(dp[i], dp[i-num]+1)或者dp[i] = max(dp[i], dp[i-num]+1)完全背包问题: 且 顺序无关 nums 在外循环、target在内循环
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
// basecase
Arrays.fill(dp, amount + 1);
dp[0] = 0;
for (int coin : coins) {
for (int i = 1; i <=amount ; i++) {
if (i >= coin) {
dp[i] = Math.min(dp[i], dp[i - coin] + 1);
}
}
}
return dp[amount] == (amount + 1) ? -1 : dp[amount];
}
474. 一和零 (01背包+顺序无关)

明确问题性质
- 最大最小值问题
- 多维费用的 0-1 背包问题, 有两个背包, 0的数量和1的数量
- 这里array中的字符,就相当于 nums[]中的数字
背包容量就是拥有的数字的个数
public int findMaxForm(String[] strs, int m, int n) {
// 这是一个多为费用的0-1背包问题,
// 有两个背包,大小是0的数量和1的数量
// sc
if (strs == null || strs.length==0) return 0;
int[][] dp = new int[m + 1][n + 1];
// 遍历nums
for (String s : strs) {
// 计算这个str有多少个0 多少个1
int ones = 0, zeros = 0;
for (char c : s.toCharArray()) {
if (c == '0') {
zeros++;
} else {
ones++;
}
}
// System.out.println("ones: " + ones);
// System.out.println("zeros: " + zeros);
// 计算不同背包容量下的可能得到的结果
for (int i = m; i >= 0; i--) {
for (int j = n; j >= 0; j--) {
if (i >= zeros && j >= ones) {
dp[i][j] = Math.max(dp[i][j], dp[i - zeros][j - ones] + 1);
}
}
}
}
return dp[m][n];
}



